运输问题案例

案例1 运输问题

某部门有3个生产同类型产品的产地，生产的产品由4个销售点出售，各工厂的生产量、各销售点的销售量以及各工厂到各销售点的单位运价（元/吨）如表1所示，求最佳调运方案？

表1 运输信息

产地\销地	B1	B2	B3	B4	产  量
A1	4	12	4	11	16
A2	2	10	3	9	10
A3	8	5	11	6	22
销  量	8	14	12	14	48

【问题分析】

 各产地的产量和各销售点的销量总和都是48，属产销平衡问题。主要研究从各产地的产品运往各销地的调运方案中选出一个最佳方案（运费最小或运输量最小或运输时间最短或路程最短等等）。

【模型假设】

1.  每个产地的产品全部运往销售地；
2. 每个销售地产品全部来自产地；

【符号设置】

• i  产地编号；
• j  销售地编号； 
• ai 产地i的产量；
• bj 销售地j的销售量；
• Xij 从产地i运往产地j的运输量；
• Cij 从产地i到销售地j的单位运费；
• Y  总运费。 

【建立模型】

将上述变量反映到表1，理清它们之间的关联，见表2

表2 各变量之间的关系

产地\销地	B1	B2	B3	B4	产  量
A1	c11,x11	c12,x12	c13,x13	c14,x14	a1
A2	c21,x21	c22,x22	c23,x23	c24,x24	a2
A3	c31,x31	c32,x32	c33,x33	c34,x34	a3
销  量	b1	b2	b3	b4

根据假设（1），有从产地1运出去的产品数量等于产地1的产量，即

 简写为

 同理有，将这三组约束，按规律归纳为

 （产量约束）

 按照假设（2），有如下销量约束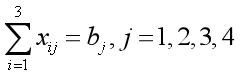（销量约束）

 变量约束

 很显然，这个问题的总运费等于各条可能的线路产生的运费之和，即

 【数学模型】

 产销平衡的数学模型如下

      【1】

 

 【1】是标准的产销平衡的运输问题的数学模型。其他类别的运输问题都是由此变形或增加条件而得。

【拓展】

（产大于销）                                                                                              （产小于销）

                                                   

                

 增加条件：体积限制、重量限制、时间限制、车型限制、产品归类限制、卸货点限制、产品比例搭配等等；

 运输路径：路径规划、流量控制等；