
1.逆序数:两个数的位置与大小顺序相反
2.二阶与三阶才能使用对角线法则计算
3.
D的某一行各元素与另一行对应元素的代数余子式(A)乘积之和为0
4.行列式的性质
1)行列式中一行(列)元素全为0,则行列式为0
2)若行列式有两行(列)成比例,则行列式为0
3)行列式的某一行(列)的元素都是两个数的和,则该行列式等于两个行列式的和(例p13)
4)互换行列式的两行(列),行列式改变符号
5)若两行(列)完全相同,则值为0
6)行列式与转置行列式的值相同 D = D的转置
7)某一行(列)的k倍加到另一行对应的元素上,值不变
5.转置行列式:行列互换
6.如果线性方程组无解或解不唯一,则D=0.
齐次方程:D = 0有非零解;D 不等于0只有零解;
齐次:只有零解说明有唯一解;有非零解说明有无穷多解。

项数:8的阶乘=40320
若n阶行列式D中等于0的个数大于n²-n。则D = 0
第二章 矩阵
1.AE =A;AB =AC,A不等于0不能推出B = C;
2.矩阵乘法不满足消去律
3.矩阵的转置满足以下运算规则:
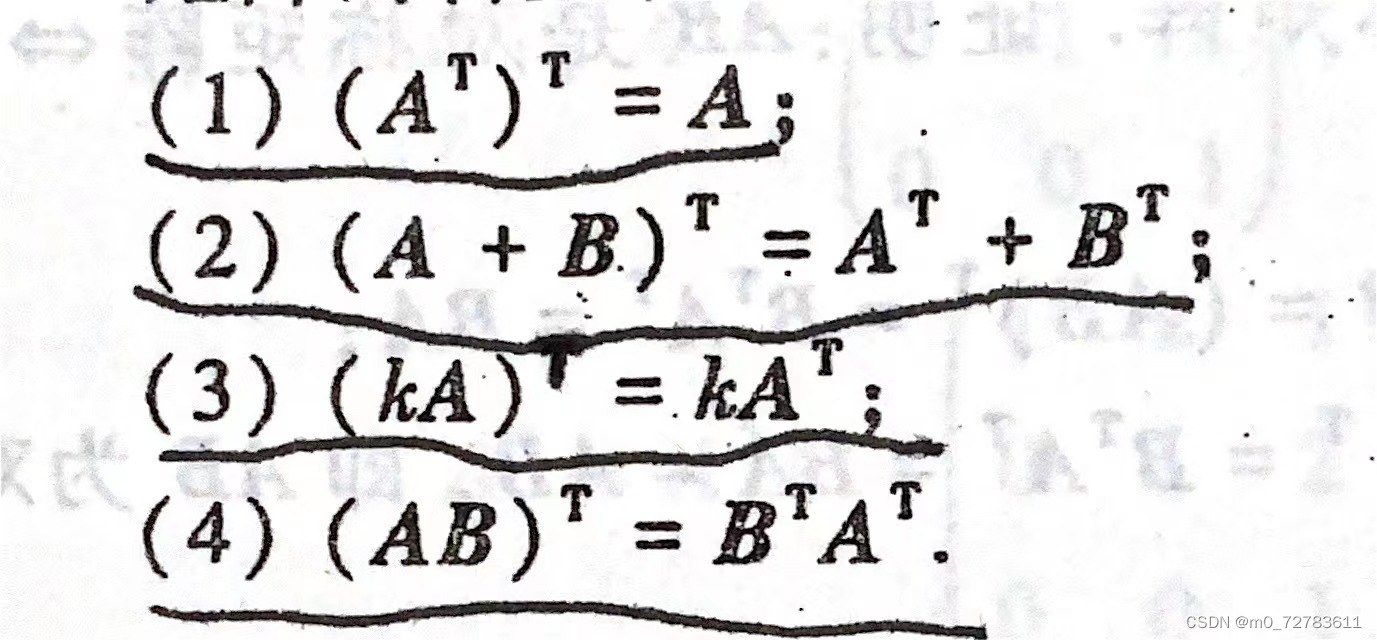
4.A是m×n的矩阵,左乘行变右乘列变:
1)对A做一次初等行变换,相当于在A的左边乘上一个相应的m阶初等矩阵;
2)对A做一次初等列变换,相当于在A的右边×一个相应的n阶初等矩阵。

 5. D = 0不可逆
5. D = 0不可逆


6. 矩阵奇数阶,则|A| = 0

7.求A的逆公式:
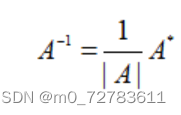
8.矩阵的初等变换
1)互换矩阵任意两行(列)的位置
2)用非零数k乘矩阵的某一行(列)元素
3)用数k乘矩阵的某行(列)各元素加到另一行(列)对应的元素上,称为矩阵的初等行(列)变换 。
4)矩阵不可以只提一行的公因子。行列式可以只提一行的公因子,但矩阵不可以,要提的话,需要把整个矩阵的公因式提出来。
9.方阵的迹:主对角线之和,又称tr(A)。
10.行最简型:所有非零行的一个非零元素都是1,且其所在列的其余元素都是零的行阶梯型。
标准型:第一个非零元素都是1,且其所在行与列的其余元素都是零的行最简型。
11.若存在n阶方阵B使AB = BA = E,称A是可逆矩阵或A可逆
12.伴随矩阵:AA* = A*A = |A|E
*伴随矩阵的构成:将矩阵A得主对角元素a,d交换位置,次对角线元素b,c添加负号即可。
13.矩阵的k阶子式:m×n矩阵A中k阶 子式的个数为C(m,k)×C(n,k)。
***矩阵的秩:矩阵中非零子式的最高阶数r成为矩阵的秩。
矩阵的性质: 零矩阵的秩为零;
零矩阵的秩为零;
若r(A) = m(或n),则称A为行(列)满秩矩阵,行满秩或列满秩都成为满秩矩阵;否则A为降秩矩阵。
对于n阶方阵:r(A)= n时为满秩,r(A)< n时为降秩。
定理1:一个m×n矩阵A的秩为r的充分必要条件是有一个r阶子式不等于0,而所有r+1阶子式都等 于 0。显然,n阶方阵A为满秩(r(A)=n <=> |A| ≠ 0)
定理2:初等变换不改变矩阵的秩
1)两行互换;2)用非零数乘矩阵的某一行
**将矩阵用初等行变换化为行阶梯形,行阶梯形矩阵中非零行的个数即为矩阵的秩。
推理1:等价矩阵具有相同的秩
推理2:设A为m×n矩阵,则对m阶可逆矩阵P,n阶可逆矩阵Q,有r(PA) = r(AQ) = r(PAQ) = r(A)
推理3:r(A) = r <=>存在可逆矩阵PQ
14.伴随矩阵的秩与矩阵的秩的关系:原矩阵秩为n 伴随矩阵秩为n; 原矩阵秩为n-1 伴随为1; 原矩阵秩小于n-1伴随为0。
15.r(A)= n <=> |A| ≠ 0 <=> A可逆
矩阵的分块:非零元素为一块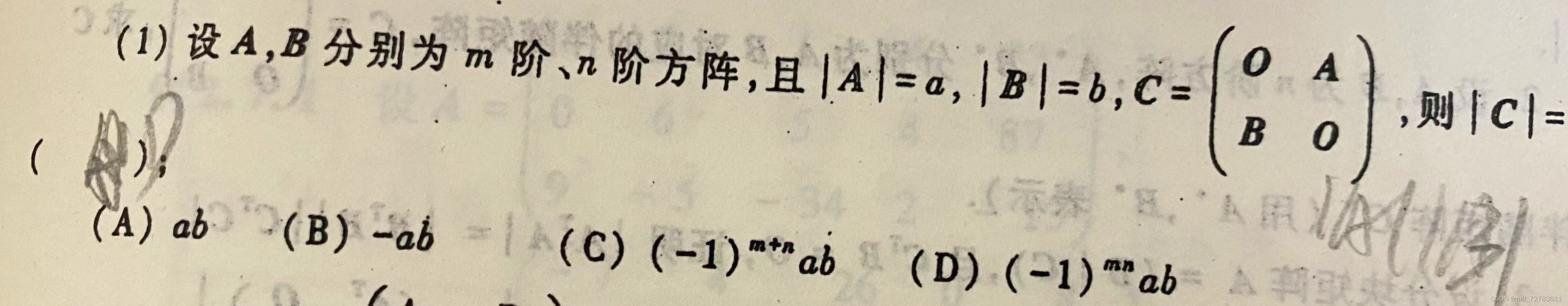
16.列矩阵×行矩阵 = 行×列矩阵,行向量×列向量 = 数;
例: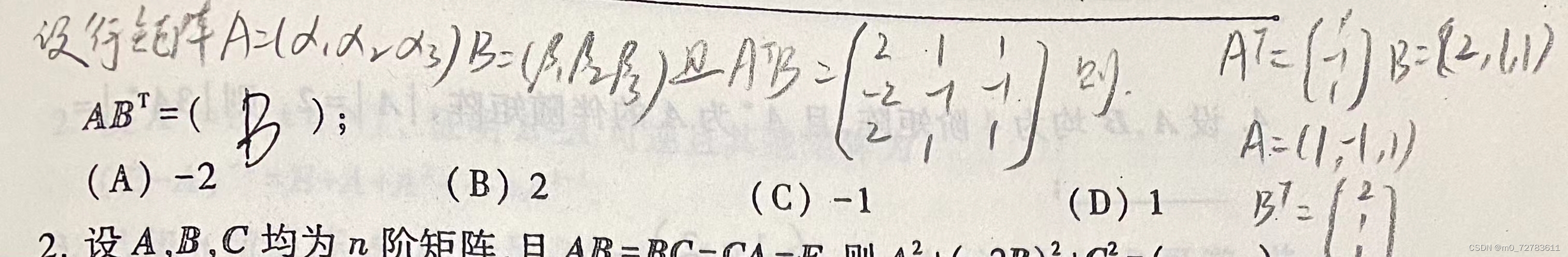
17.可逆矩阵可以分解为有限个初等矩阵的乘积
第三章 向量方程组
1.齐次线性方程组非零解条件:

2.求通解:
3求解线性方程:
通过对增广矩阵进行初等行变换实现.实现过程:利用矩阵的初等行变换将A化为行阶梯形(消元过程),再继续施行初等行变换将行阶梯形化为行最简形,有最简式读出。
*仅限于初等行变换,这种变换不改变方程组的同解性。
4.线性方程组Ax = b有解的充要条件是系数矩阵A与增广矩阵A的秩相等,即r(A)= r(B),当r(A)= r(B)= n时,方程组有唯一解;当r(A)= r(B)< n 时,方程组有无穷多解。
5.
6.
(1)当向量组所含向量的个数与向量的维数相等时,该向量组构成的行列式不为零的充分必要条件是该向量组线性无关;
(2)当向量组所含向量的个数多于向量的维数时,该向量组一定线性相关;
(3)通过向量组的秩研究向量组的相关性。若向量组的秩等于向量的个数,则该向量组是线性无关的;若向量组的秩小于向量的个数,则该向量组是线性相关的。
(4)满秩(r(A)=n),对应的方程组有唯一解,因此向量组线性无关。
(5)如果向量组a线性无关,则其接长向量组b必线性无关
(6)若向量组1可有向量组2表示,且s>t,则1线性相关。
(7)可逆矩阵行列式不为0,所以其向量组是线性无关的。
7.向量组的值:等价的向量组具有相同的秩;矩阵A的秩等于它的向量组的秩,也等于他的行向量的秩。








 本文详细介绍了线性代数中的关键概念,包括行列式、矩阵的性质、秩、逆矩阵、线性方程组的解法及向量组的相关性。讨论了行列式的性质,如零行列式、行列式的性质以及行列式的计算规则。同时,阐述了矩阵的初等变换、秩、可逆性与伴随矩阵的关系,并探讨了线性方程组的解的存在性和唯一性条件。此外,还涉及向量组的线性相关性和线性无关性的判断。
本文详细介绍了线性代数中的关键概念,包括行列式、矩阵的性质、秩、逆矩阵、线性方程组的解法及向量组的相关性。讨论了行列式的性质,如零行列式、行列式的性质以及行列式的计算规则。同时,阐述了矩阵的初等变换、秩、可逆性与伴随矩阵的关系,并探讨了线性方程组的解的存在性和唯一性条件。此外,还涉及向量组的线性相关性和线性无关性的判断。
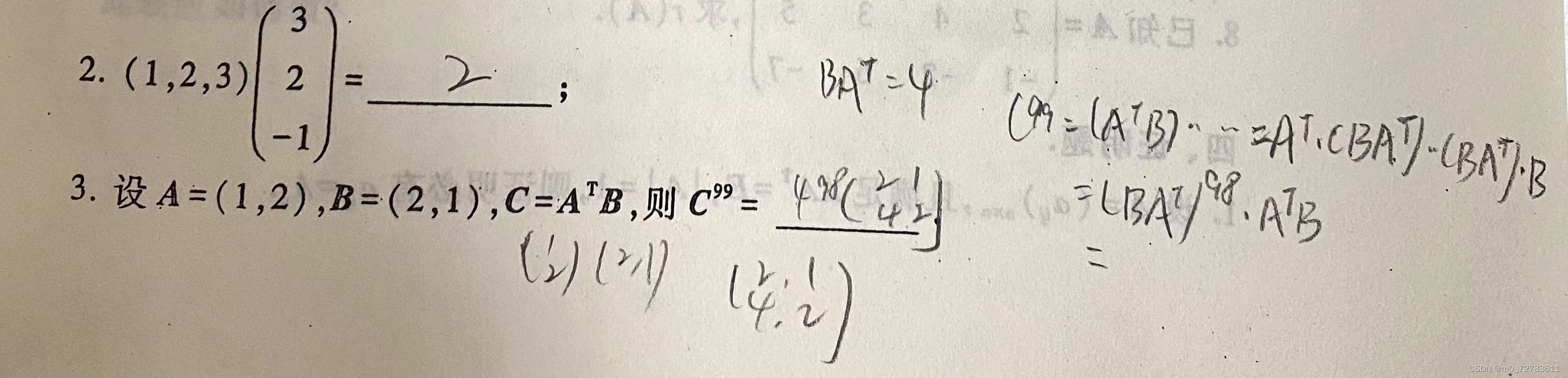
















 1624
1624

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








