求解线性方程组的直接法、gauss-sidel迭代法

、实验原理

根据求解线性方程组的三角分解法、gauss-sidel迭代法等相关知识和算法编程完成本实验

二、实验内容

     见本课教材：附录1上机作业

必做题：程序12，程序16

     1）用程序12验证如下方程组

   

2）用程序16验证如下方程组

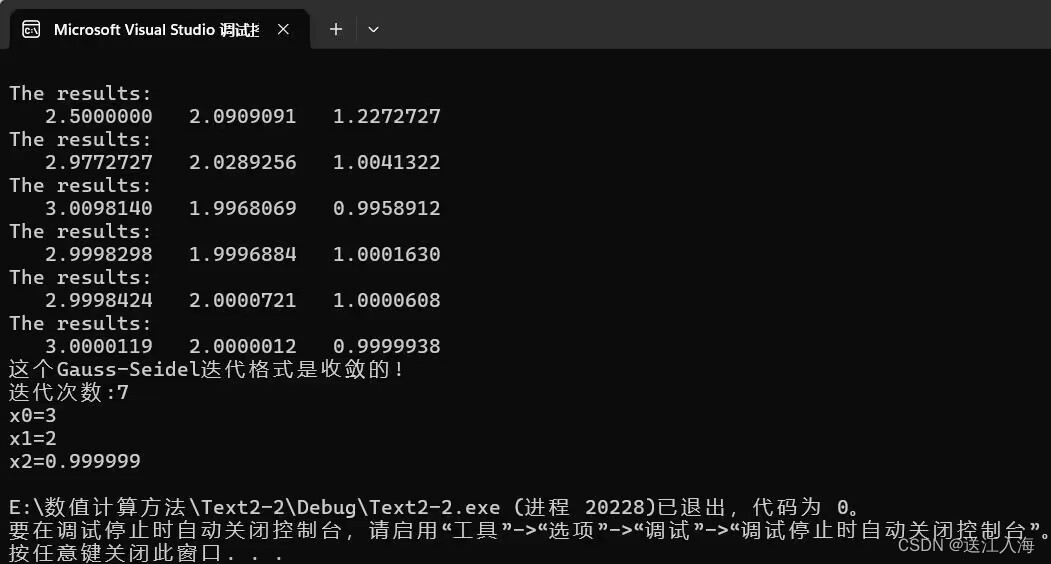
任取初始向量x(0)=(0, 0, 0)T ,

计算       x(1)=(2.5, 2.090909, 1.227272)T , …,

              x(5)=(2.99984,  2.000072,  1.000061)T

三、实验过程（可以文字说明+运行结果截图）

1）Doolittle分解法

实验说明：

数据说明：

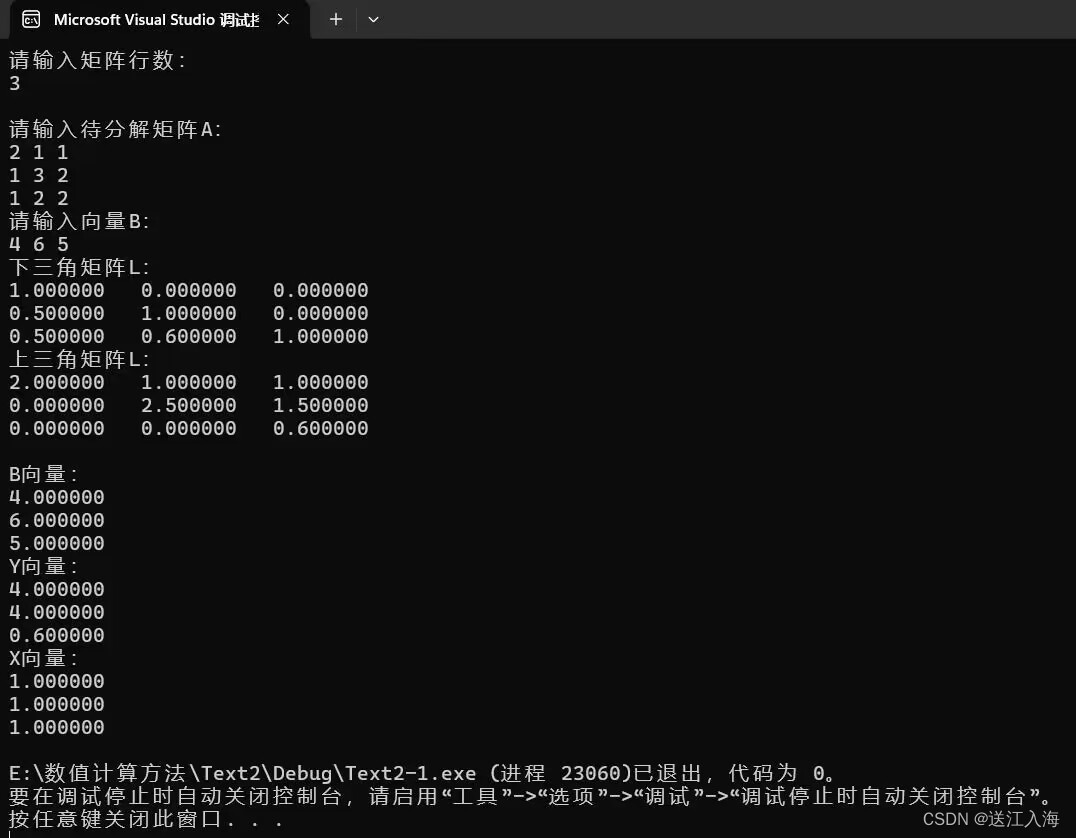
1.矩阵A：一个n×n的待分解矩阵，用户需要输入此矩阵的元素。

2.向量B：一个长度为n的向量，用户需要输入此向量的元素。

3.矩阵L：一个n×n的下三角矩阵，初始时对角线元素为1，其余元素由算法计算得出。

4.矩阵R: 一个n×n的上三角矩阵，初始时对角线元素为A的对角线元素，其余元素由算法计算出。

5.向量X: 一个长度为n的向量，算法求解得到的最终解。

6.向量Y: 一个长度为n的向量，中间计算步骤的结果。

代码说明

1.输入矩阵尺寸：

用户输入矩阵 A 的行数和列数，即矩阵的尺寸 n。

2.输入矩阵 A 和向量 B：

用户输入矩阵 A 的元素和向量 B 的元素。

3.初始化矩阵：

调用 InitMatrix() 初始化矩阵 L 和 R。对角线元素和上下三角部分根据规则初始化。

4.Doolittle 分解：

调用 Doolittle() 执行 Doolittle 分解。通过前向消去和后向替代法求解线性方程组。

5.打印结果：、调用 print() 打印下三角矩阵 L、上三角矩阵 R、向量 B、向量 Y 和向量 X

算法说明

1.初始化矩阵：

初始化 L 为单位矩阵， R 为零矩阵。

2.计算上三角矩阵 R：

通过从左到右的方式，计算矩阵 R 的元素。公式如下：

3.计算下三角矩阵 L：

通过从上到下的方式，计算矩阵 L 的元素。公式如下：

4.前向消去：

解方程 LY=B 得到向量 Y：

5.后向替代：

解方程 UX=Y 得到向量 X：

运行截图：

2）程序16: Gauss-Seidel 迭代法

实验说明：

数据说明：

1.矩阵 A：

一个N×N 的系数矩阵，在这个例子中是一个 3x3 矩阵。

2.向量 b：

一个长度为 N 的常数向量。

3.初始向量x：

一个长度为 N 的初始猜测向量，初始值设为零向量。

4.迭代次数和收敛条件：

最大迭代次数设为 1000 次，收敛误差阈值为 0.0001。

代码说明

1.定义矩阵和向量：

定义并初始化系数矩阵 A、常数向量 b 和初始向量 x。

2.调用 Gauss-Seidel 迭代函数：

调用 GS(dim, A, b, x) 函数执行迭代，解线性方程组。

3.打印结果：

打印最终得到的解向量 x。

算法说明

1.初始化：

初始化解向量x和临时向量

2.迭代更新：

对每个分量

进行更新，使用最新计算出的x值。迭代公式如下：

3.收敛判定：

如果在某次迭代中，所有分量的更新值小于阈值，则判定迭代收敛。

4.打印迭代次数和结果：

如果迭代收敛，则打印迭代次数和最终结果。

如果迭代未收敛，提示可能不收敛。

运行截图：