✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
⛄ 内容介绍
卡尔曼滤波可以通过运动方程及概率统计实现对一般事物发展的预测,因为不需要追溯历史数据,只需根据上一时刻的状态来预测下一时刻的状态,所以在故障诊断,巡航制导等方面应用广泛.基于此,将卡尔曼滤波作为预测模型来实现车辆的行车轨迹预测.首先阐述了卡尔曼滤波的预测过程及公式,其次将小车的运动区分为直线运动和转向运动,并通过简化阿克曼转向理论构建小车的运动模型,最后采样三次插值算法实现赛车路径规划。
⛄ 部分代码
clear;
clc;
load 'track_352.mat';%原始赛道信息
load 'body.mat';%车辆信息
load 'dynamic_constrains.mat';%动力学约束
safe_dist = 2;%距离障碍物安全距离
%% 平滑插值赛道
tolerance = 10;%先线性插值,去掉大间隙
[track_x,track_y] = track_smooth_linear(track_x,track_y,tolerance);
tolerance = 3;%然后三次样条线插值,达到最终步长
[track_x,track_y] = track_smooth_spline(track_x,track_y,tolerance);
clear tolerance;
%% 求得与赛道长度对应的样条线参数
[c,~] = size(track_x);
[spline_A] = spline_matrix_gen(c);%样条线求解矩阵,要留在内存中,加速计算
para_x = spline_A * track_x;%x三次样条参数
para_y = spline_A * track_y;%y三次样条参数
%% 单位切向量
[vector] = vector_gen(para_x,para_y,c);
%% 绘制中心线、左右边界及障碍物
draw_track(track_x,track_y,vector,track_w,obs_x,obs_y,c);
%% QP优化初始化
alpha_out = zeros(c,1);%本次次迭代结果
alpha_last = zeros(c,1);%上一次迭代结果
[lb,ub] = init_lub(track_w,body.Wb,c);%上下界初始化
[Aieq,bieq] = init_ieq(track_x,track_y,obs_x,obs_y,safe_dist,c);%有关障碍物的不等式约束初始化
stop_inter_thres = c * 0.01;%每一次迭代后所有点上横向改变平方和,每一个点上差别不超过1厘米
inter_val = 100000;%初始停止条件数值
path_cnt = 0;%迭代次数
%% QP优化
%不下降时停止迭代
tic;
while inter_val >= stop_inter_thres
[alpha_out,alpha_last,lb,ub,track_x,track_y,vector] = QP_optimization(spline_A,alpha_out,alpha_last,lb,ub,Aieq,bieq,track_x,track_y,vector,c);
inter_val = sum(alpha_out.^2);
path_cnt = path_cnt + 1;
end
[c_alpha,~] = size(alpha_out);
if c_alpha == 0
alpha_out = zeros(c,1);%以防无解
end
clear c_alpha;
path_t = toc;
clc;
clear stop_inter_thres inter_val lb ub Aieq bieq;
%% 生成最优路径及其信息
draw_optimised_path(track_x,track_y,vector,alpha_out,'m');%绘制最优路径
[track_x,track_y] = path_gen(track_x,track_y,vector,alpha_out);%保存最优路径
[path_distance] = path_distance_calculate(track_x,track_y,c);%沿最优路径距离
para_x = spline_A * track_x;
para_y = spline_A * track_y;
[vector] = vector_gen(para_x,para_y,c);
[phi] = phi_accum_gen(vector,c);%参考车辆航向角
[curvature_res] = get_curvature(para_x,para_y,c);%参考曲率
clear obs_x obs_y obs_w safe_dist alpha_out alpha_last;
%% 速度规划
[apex_location,apex_cnt] = get_apex(curvature_res,c);%标记Apex点
vmax = 40;%限制最高直线车速
[vel_geo] = geometry_vel_calculate(curvature_res,vmax,ay_para,c);%计算几何速度限制
[vel_forward] = forward_calculate(apex_location,apex_cnt,vel_geo,curvature_res,path_distance,acc_para,ay_para,c);%加速限制
[vel_backward] = backward_calculate(apex_location,apex_cnt,vel_geo,curvature_res,path_distance,brk_para,ay_para,c);%减速限制
vel_profile = min(vel_geo,min(vel_forward,vel_backward));%三种取最小值
[vel_flying] = init_vel_calculate(vel_profile,vel_profile(end),acc_para,ay_para,path_distance,curvature_res,c);%飞驰圈速度规划
delta_profile = atan(curvature_res * body.l / 1000);
clear apex_location apex_cnt vel_geo vel_forward vel_backward acc_para ay_para brk_para vmax vel_profile;
%% 绘制速度规划
figure(2);
clf;
subplot(2,1,1);
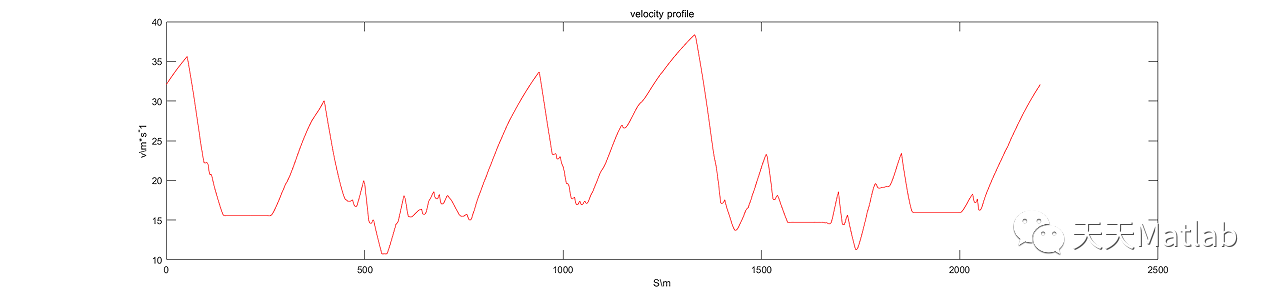
plot(path_distance,vel_flying,'r');%绘制速度-距离规划
xlabel('S\\m');
ylabel('v\\m*s^-1');
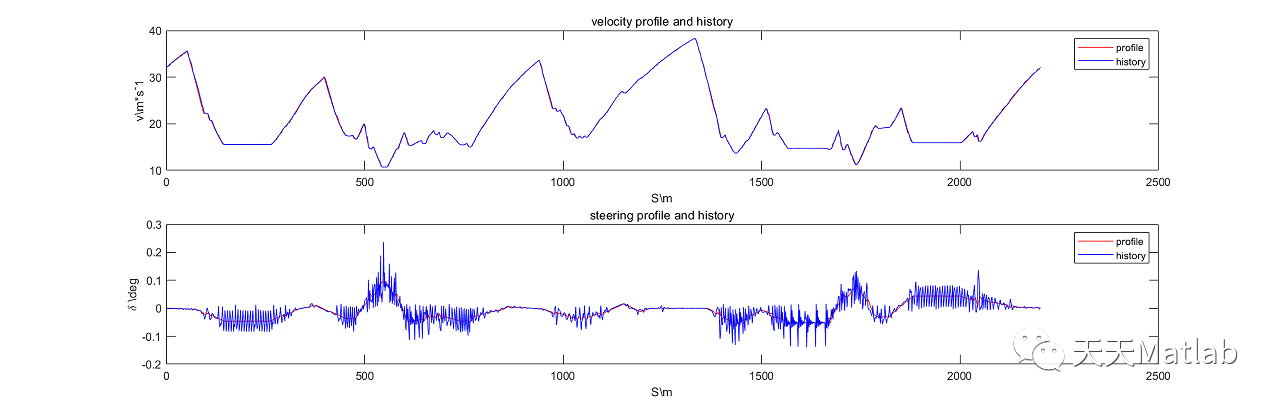
title('velocity profile and history');
subplot(2,1,2);
plot(path_distance,delta_profile,'r');%绘制方向盘转角-距离规划
xlabel('S\\m');
ylabel('\delta \\deg');
title('steering profile and history');
%% 仿真参数设置
dt = 0.1;%时间间隔
np = 20;%预测步长
nc = 10;%控制步长
nx = 3;%状态量数目
nu = 2;%控制量数目
%% 参考量设置
state_ref = [track_x,track_y,phi,curvature_res,vel_flying,path_distance];
%% 物理限制设置
u_max = [40;0.5];
u_min = [2;-0.5];
du_max = [0.2;0.2];
du_min = [-0.2;-0.2];
%% 车辆参数及状态设置
l = body.l / 1000;
target_v = vel_flying(1);%期望速度
delta = 0;%当前转向角
travel = 0;%当前里程
control_d = [0;0];%上一时刻控制偏差
control_act = [target_v;delta];%当前实际控制值
control = [control_act];%储存实际控制指令
x_d = [0;0;0];%当前状态偏差
x_act = [track_x(1);track_y(1);phi(1)];
x_res = [x_act];%储存实际状态
travel_history = [travel];%里程表历史
%% 权重矩阵及观测矩阵生成
[Qt,Rt,Ct,rou] = weight_matrix_gen(nx,nu,np,nc);
%%
index = 0;
tic;
mpc_cnt = 0;
while index < c - 1
% 矩阵生成↓↓↓
[At,Bt] = sequential_increment_matrix_gen(x_act,control_act,Ct,np,nc,body,dt);
% 求当前点偏差↓↓↓
[x_d,index] = find_state_ref_err(para_x,para_y,state_ref,x_act,travel,c);
target_v = vel_flying(index);
% 求当前约束↓↓↓
[A_eqst,b_eqst,A_ieqst,b_ieqst,lb,ub] = get_constrains(u_max,u_min,du_max,du_min,control_act,nc,nu);
% 求最优控制量偏差↓↓↓
yita = [x_d;control_d];
H = [Bt' * Qt * Bt + Rt,zeros(size(Bt,2),1);zeros(1,size(Bt,2)),rou];
H = H + H';%quadprog程序是求1/2H,故将其变为二倍
F = [2 * yita' * At' * Qt * Bt,0]';%最后一个对应松弛变量
U_out = quadprog(H,F,A_ieqst,b_ieqst,A_eqst,b_eqst,lb,ub);
% 求最优控制量↓↓↓
delta_des = delta_profile(index);%该点处期望转向角
control_act = [target_v;delta_des] + control_d + [U_out(1);U_out(2)];%用得到的控制偏差和上一步的控制偏差修正
control_act(1) = min(control_act(1),target_v);
control = [control,control_act];%储存
control_d = [U_out(1);U_out(2)];%更新当前的控制偏差
% 更新并储存状态↓↓↓
[x_act,travel] = update_state(x_act,control_act,dt,l,travel);
x_res = [x_res,x_act];%储存
mpc_cnt = mpc_cnt + 1;
travel_history = [travel_history;travel];%储存里程历史
end
mpc_t = toc;
clc;
clear nc np nu nx index A_eqst A_ieqst b_eqst b_ieqst At Bt Ct dt du_max du_min ...
H F control_d control_act delta delta_des l lb ub target_v travel u_max u_min U_out x_act ...
x_d yita state_ref t Qt Rt rou cnt;
x_res = x_res';
control = control';
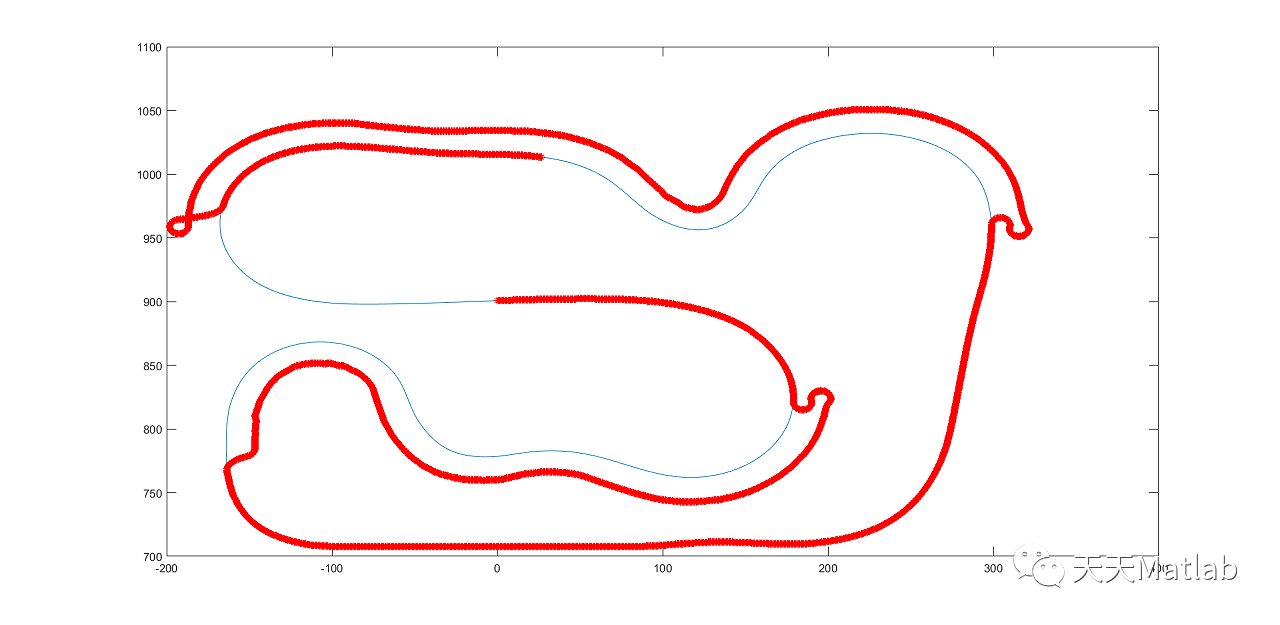
%% 绘制MPC历史
draw_body_attitude(x_res,control,travel_history,body);
%% 打印计算时间
fprintf('路径优化:迭代%d次,耗时%f秒\n',path_cnt,path_t);
fprintf('MPC控制:迭代%d次,耗时%f秒\n',mpc_cnt,mpc_t);
clear path_cnt path_t mpc_cnt mpc_t;
%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%路径规划子函数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 生成样条线求解矩阵
function [spline_A] = spline_matrix_gen(c) %[a;b;c;d] = A * y
%%%%%%%% 输入D
D = 3 * [eye(c - 2),zeros(c - 2,2)] -6 * [zeros(c - 2,1),eye(c - 2),zeros(c - 2,1)] + 3 * [zeros(c - 2,2),eye(c - 2)];
tmp = [-3,3,zeros(1,c - 4),3,-3];
D = [tmp;D;tmp];
%%%%%%%% c
A = eye(c) + 0.5 * [zeros(c - 1,1),eye(c - 1);zeros(1,c)];
A = A + A';
A(1,c - 1) = 0.5;
A(c,2) = 0.5;
matrix_c = 2 * A \ D;
%%%%%%%% a
matrix_a = eye(c);
%%%%%%%% b
Ab = eye(c) / 6 + [zeros(c - 1,1),eye(c - 1) / 3;zeros(1,c)];
Ab(c,2) = 1 / 3;
Aby = [-eye(c - 1),zeros(c - 1,1)] + [zeros(c - 1,1),eye(c - 1)];
Aby = [Aby;Aby(1,:)];
matrix_b = Ab / A * D + Aby;
%%%%%%%% d
Ad = eye(c) / 6 - [zeros(1,c);[eye(c - 1) / 6,zeros(c - 1,1)]];
Ad(1,c - 1) = -1 / 6;
matrix_d = Ad / A * D;
%%%%%%% 整合
zero = zeros(c);
A_sig = [matrix_a,zero,zero,zero
zero,matrix_b,zero,zero
zero,zero,matrix_c,zero
zero,zero,zero,matrix_d];
Dy = [eye(c);eye(c);eye(c);eye(c)];
spline_A = A_sig * Dy;
end
%% 生成切向量
function [vector] = vector_gen(para_x,para_y,c)
select_b = [zeros(c),eye(c),zeros(c),zeros(c)];
Dx = select_b * para_x;
Dy = select_b * para_y;
vector = zeros(c,2);%该点处切向量
for i = 1:c%切向量
len = sqrt(Dx(i)^2 + Dy(i)^2);
vector(i,1) = Dx(i) / len;
vector(i,2) = Dy(i) / len;
if isnan(vector(i,1))%滤掉NaN
vector(i,1) = vector(i - 1,1);
end
if isnan(vector(i,2))
vector(i,2) = vector(i - 1,2);
end
if (i>1)&&(vector(i,1) - vector(i - 1,1) > 1.8)%滤掉过大跳变
vector(i,1) = vector(i - 1,1);
end
if (i>1)&&(vector(i,2) - vector(i - 1,2) > 1.8)
vector(i,2) = vector(i - 1,2);
end
end
end
%% 绘制原始赛道
function [] = draw_track(track_x,track_y,vector,track_w,obs_x,obs_y,c)
figure(1);
clf;
alpha_r = track_w / 2 *ones(c,1);
alpha_l = -alpha_r;
[x_l,y_l] = path_gen(track_x,track_y,vector,alpha_l);
[x_r,y_r] = path_gen(track_x,track_y,vector,alpha_r);
plot(track_x,track_y,'k--');
hold on;
plot(x_l,y_l,'r');
hold on;
plot(x_r,y_r,'b');
hold on;
plot(track_x(1),track_y(1),'b*');
hold on;
plot(obs_x,obs_y,'r*');
end
%% 生成HF矩阵
function [H,F] = HF_gen(spline_A,para_x,para_y,track_x,track_y,vector,c)
select_b = [zeros(c),eye(c),zeros(c),zeros(c)];
select_c = [zeros(c),zeros(c),eye(c),zeros(c)];
A = select_c * spline_A;
Dx = select_b * para_x;
Dy = select_b * para_y;
base = (Dx.^2 + Dy.^2).^3;
Pxx = diag(Dy.^2 ./ base);
Pxy = diag(-2 * Dx .* Dy ./ base);
Pyy = diag(Dx.^2 ./ base);
Vx = diag(vector(:,2));%alpah左负右正
Vy = diag(-vector(:,1));
Tc = 2 * A;
Tnx = 2 * A * Vx;
Tny = 2 * A * Vy;
H = Tnx' * Pxx * Tnx ...
+ Tny' * Pxy * Tnx + ...
Tny' * Pyy * Tny;
H = H + H';
F = 2 * Tnx' * Pxx' * Tc * track_x ...
+ Tny' * Pxy' * Tc * track_x + Tnx' * Pxy' * Tc * track_y ...
+ 2 * Tny' * Pyy' * Tc * track_y;
F = F';
end
%% 上下限初始化
function [lb,ub] = init_lub(track_w,wb,c)
hard_bound = track_w / 2 - wb / 2000;
lb = -hard_bound * ones(c,1);
ub = hard_bound * ones(c,1);
end
%% 更新上下限
function [lb,ub] = update_lub(lb,ub,alpha)
lb = lb - alpha;
ub = ub - alpha;
end
%% 不等式约束初始化
function [Aieq,bieq] = init_ieq(track_x,track_y,obs_x,obs_y,safe_dist,c)
[num_obs,~] = size(obs_x);
%确定障碍物位置
distance = zeros(c,num_obs);
for i = 1:c
for k = 1:num_obs
distance(i,k) = (track_x(i) - obs_x(k))^2 + (track_y(i) - obs_y(k))^2;
end
end
pos = zeros(num_obs,1);
for k = 1:num_obs
pos(k) = find(distance(:,k)==min(min(distance(:,k))));
end
%判断障碍物左右位置并生成约束
%把障碍物处的硬边界换成安全距离
Aieq = zeros(num_obs,c);
bieq = zeros(num_obs,1);
for k = 1:num_obs
if (track_x(pos(k)) - obs_x(k) + track_y(pos(k)) - obs_y(k)) >=0%障碍物在左(下)边
Aieq(k,pos(k)) = -1;
bieq(k) = -safe_dist + sqrt(distance(pos(k),k));
else%障碍物在右(上)边
Aieq(k,pos(k)) = 1;
bieq(k) = -safe_dist + sqrt(distance(pos(k),k));
end
end
end
%% 更新不等式约束
function [Aieq,bieq] = ieq_update(Aieq,bieq,alpha)
[posx,posy] = find(Aieq);
Aieq = Aieq;
[c,~] = size(posy);
delta_alpha = zeros(c,1);
trans = zeros(c);
for i = 1:c
delta_alpha(i) = alpha(posy(i));
trans(i,i) = Aieq(posx(i),posy(i));
end
bieq = bieq - trans * delta_alpha;
end
%% 生成等式约束
function [Aeq,beq] = eq_gen(c) %保证始末点连续
Aeq = zeros(1,c);
Aeq(1) = 1;
Aeq(c) = -1;
beq = [0];
end
%% 生成路径
function [p_x,p_y] = path_gen(track_x,track_y,vector,alpha)
p_x = track_x + alpha .* vector(:,2);
p_y = track_y - alpha .* vector(:,1);
end
%% 生成累积航向角
function [phi_out] = phi_accum_gen(vector,c)
phi_new = zeros(c,1);
for i = 1:c%转换为0-360范围
phi_abs = abs(atan(vector(i,2) / vector(i,1)));
if (vector(i,1) > 0) && (vector(i,2) >= 0)
phi_new(i) = phi_abs;
end
if (vector(i,1) <= 0) && (vector(i,2) > 0)
phi_new(i) = pi - phi_abs;
end
if (vector(i,1) < 0) && (vector(i,2) <= 0)
phi_new(i) = pi + phi_abs;
end
if (vector(i,1) >= 0) && (vector(i,2) < 0)
phi_new(i) = 2 * pi - phi_abs;
end
end
phi_new = phi_new * 180 / pi;
phi_out = zeros(c,1);
phi_out(1) = phi_new(1);
for i = 2:c
diff = phi_new(i) - phi_out(i - 1);
if abs(diff) > 200
phi_new = phi_new - diff;
end
phi_out(i) = phi_new(i);
end
phi_out = phi_out * pi / 180;
end
%% 绘制优化后路径
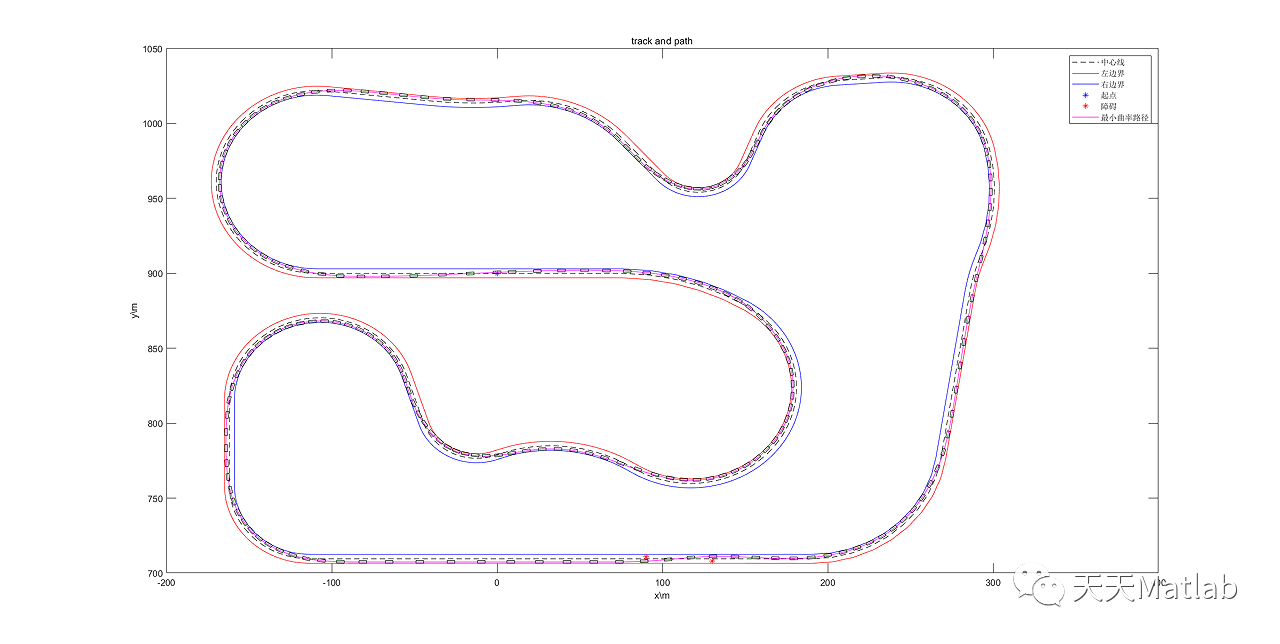
function [] = draw_optimised_path(track_x,track_y,vector,alpha,color_inpt)
figure(1);
[p_x,p_y] = path_gen(track_x,track_y,vector,alpha);
plot(p_x,p_y,color_inpt);
xlabel('x\\m');
ylabel('y\\m');
title('track and path');
end
%% 线性插值赛道 前处理
function [x_out,y_out] = track_smooth_linear(track_x,track_y,tolerance)
[c,~] = size(track_x);
x_out = [];
y_out = [];
for i = 1:c - 1
len = sqrt((track_x(i + 1) - track_x(i))^2 + (track_y(i + 1) - track_y(i))^2);
if len >= tolerance
n = ceil(len / tolerance);
y_ran = track_y(i + 1) - track_y(i);
x_ran = track_x(i + 1) - track_x(i);
temp_x = zeros(n,1);
temp_y = zeros(n,1);
for k = 1:n
val = (k - 1) / n;
temp_x(k) = track_x(i) + val * x_ran;
temp_y(k) = track_y(i) + val * y_ran;
end
x_out = [x_out;temp_x];
y_out = [y_out;temp_y];
else
x_out = [x_out;track_x(i)];
y_out = [y_out;track_y(i)];
end
end
x_out = [x_out;track_x(i + 1)];
y_out = [y_out;track_y(i + 1)];
end
%% 三次样条插值赛道 第二次处理
function [x_out,y_out] = track_smooth_spline(track_x,track_y,tolerance)
[c,~] = size(track_x);
[spline_A] = spline_matrix_gen(c);
para_x = spline_A * track_x;
para_y = spline_A * track_y;
select_c = 2 * [zeros(c),zeros(c),eye(c),zeros(c)];
Mx = select_c * para_x;
My = select_c * para_y;
x_out = [];
y_out = [];
for i = 1:c - 1
len = sqrt((track_x(i + 1) - track_x(i))^2 + (track_y(i + 1) - track_y(i))^2);
if len >= tolerance
n = ceil(len / tolerance);
temp_x = zeros(n,1);
temp_y = zeros(n,1);
for k = 1:n
val = (k - 1) / n;
temp_x(k) = Mx(i) * (1 - val)^3 / 6 ...
+ Mx(i + 1) * (val - 0)^3 / 6 ...
+ (track_x(i) - Mx(i) / 6) * (1 - val) ...
+ (track_x(i + 1) - Mx(i + 1) / 6) * (val - 0);
temp_y(k) = My(i) * (1 - val)^3 / 6 ...
+ My(i + 1) * (val - 0)^3 / 6 ...
+ (track_y(i) - My(i) / 6) * (1 - val) ...
+ (track_y(i + 1) - My(i + 1) / 6) * (val - 0);
end
x_out = [x_out;temp_x];
y_out = [y_out;temp_y];
else
x_out = [x_out;track_x(i)];
y_out = [y_out;track_y(i)];
end
end
x_out = [x_out;track_x(i + 1)];
y_out = [y_out;track_y(i + 1)];
end
%% QP优化子程序
function [alpha_out,alpha_last,lb,ub,track_x,track_y,vector] = QP_optimization(spline_A,alpha,alpha_last,lb,ub,Aieq,bieq,track_x,track_y,vector,c)
alpha = alpha_last * 1 / 3 + alpha * 2 / 3;%更新alpha
[track_x,track_y] = path_gen(track_x,track_y,vector,alpha);%更新中心线(这次优化的参考),利用上次的参考和坐标
para_x = spline_A * track_x;
para_y = spline_A * track_y;
[vector] = vector_gen(para_x,para_y,c);%更新向量
[H,F] = HF_gen(spline_A,para_x,para_y,track_x,track_y,vector,c);%更新HF
[lb,ub] = update_lub(lb,ub,alpha);%更新上下限
[Aeq,beq] = eq_gen(c);
[Aieq,bieq] = ieq_update(Aieq,bieq,alpha);%更新不等式约束
alpha_last = alpha;
alpha_out = quadprog(H,F,Aieq,bieq,Aeq,beq,lb,ub);%(这次优化后的坐标)
end
%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%速度规划子函数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 计算路径长度
function [distance] = path_distance_calculate(track_x,track_y,c)
distance = zeros(c,1);
for i = 2:c
distance(i) = sqrt((track_x(i) - track_x(i - 1))^2 + (track_y(i) - track_y(i - 1))^2) + distance(i - 1);
end
end
%% 获取曲率
function [curvature] = get_curvature(para_x,para_y,c)
select_b = [zeros(c),eye(c),zeros(c),zeros(c)];
select_c = [zeros(c),zeros(c),eye(c),zeros(c)];
Dx = select_b * para_x;
Dy = select_b * para_y;
DDx = 2 * select_c * para_x;
DDy = 2 * select_c * para_y;
base = (Dx.^2 + Dy.^2).^1.5;
curvature = (Dx .* DDy - Dy .* DDx) ./ base;
end
%% 标记Apex点
function [apex_location,apex_cnt] = get_apex(curvature_res,c)
apex = zeros(c,1);
apex(1) = 1;
apex(c) = 1;
for i = 2:c - 1%标记Apex点
if ((curvature_res(i + 1) - curvature_res(i)) * (curvature_res(i) - curvature_res(i - 1)) <= 0)% && (sum(apex(i - 4:i)) == 0)
apex(i) = 1;
end
end
apex_location = find(apex);
[apex_cnt,~] = size(apex_location);
end
%% 卡尔曼滤波
function [vector_out] = smooth_curvature_kalman(vector_in,c,Q,R)
vector_out = zeros(c,1);
x = vector_in(1);
P = 100;
% curvature_res(1) = x;
for i = 1:c
xnp = x;
Pnp = P + Q;
G = Pnp / (Pnp + R);
x = xnp + G * (vector_in(i) - xnp);
P = (1 - G) * Pnp;
vector_out(i) = x;
end
end
%% 几何速度(查表法)
function [vel_geo] = geometry_vel_calculate(curvature_res,vmax,ay_para,c)
vel_geo = zeros(c,1);
vel_ran = [5:0.001:vmax]';
k_v = polyval(ay_para,vel_ran) ./ vel_ran.^2;
[kv_num,~] = size(k_v);
for i = 1:c
j = kv_num;
while abs(curvature_res(i)) >= k_v(j)
j = j - 1;
end
vel_geo(i) = vel_ran(j - 1);
end
end
%% 前向计算加速度
function [vel_forward] = forward_calculate(apex_location,apex_cnt,vel_geo,curvature,path_distance,acc_para,ay_para,c)
vel_forward = zeros(c,1);
vel_forward(1) = vel_geo(1);
for i = 1:apex_cnt - 1
v_ref = min(vel_geo(apex_location(i)),vel_forward(apex_location(i)));%Apex点参考速度和上一步得出速度最小值
for j = apex_location(i) + 1:apex_location(i + 1)
ax_max = polyval(acc_para,v_ref);
ay_max = polyval(ay_para,v_ref);
delta_s = path_distance(j) - path_distance(j - 1);
if ((v_ref^2 * curvature(j - 1)) / (ay_max))^2 < 1%确保车辆不失稳(安全域)
v_ref = sqrt(v_ref^2 + 2 * delta_s * ax_max * sqrt(1 - ((v_ref^2 * curvature(j - 1)) / (ay_max))^2));
end
vel_forward(j) = v_ref;
end
end
vel_forward(c) = v_ref;
end
%% 反向计算减速度
function [vel_backward] = backward_calculate(apex_location,apex_cnt,vel_geo,curvature,path_distance,brk_para,ay_para,c)
vel_backward = zeros(c,1);
vel_backward(c) = vel_geo(c);
for i = apex_cnt + 1 - [1:apex_cnt - 1]
v_ref = min(vel_geo(apex_location(i)),vel_backward(apex_location(i)));%Apex点参考速度和上一段制动结束速度最小值
for j = apex_location(i) - [1:apex_location(i) - apex_location(i - 1)]
ax_max = polyval(brk_para,v_ref);
ay_max = polyval(ay_para,v_ref);
delta_s = path_distance(j + 1) - path_distance(j);
if ((v_ref^2 * curvature(j + 1)) / (ay_max))^2 < 1%确保车辆不失稳(安全域)
v_ref = sqrt(v_ref^2 + 2 * delta_s * ax_max * sqrt(1 - ((v_ref^2 * curvature((j + 1)) / (ay_max))^2)));
end
vel_backward(j) = v_ref;
end
end
end
⛄ 运行结果
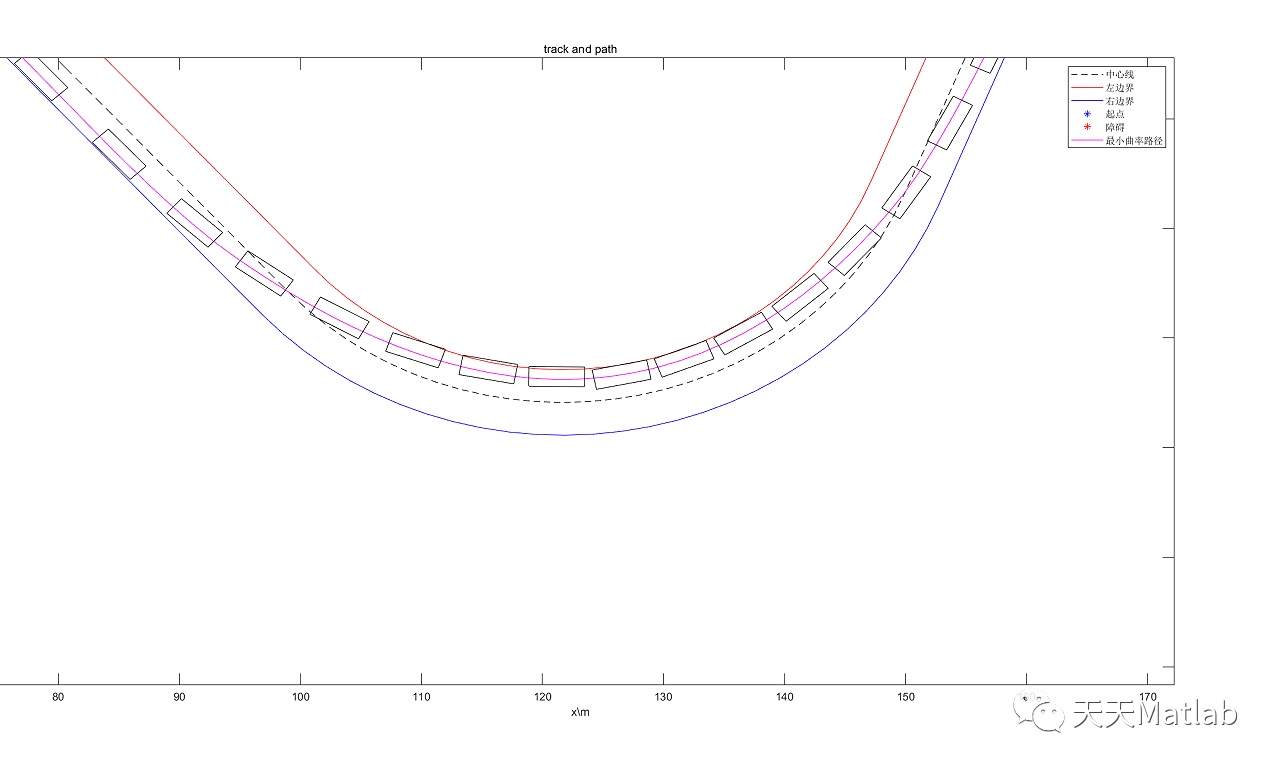
⛄ 参考文献
[1]李蕾, 喻春晖, 刘小明. 三次样条插值卡尔曼滤波分光光度法同时测定NO_3~-和NO_2~-的研究[J]. 赣南师范学院学报, 1997(6):4.
[2]周文霞, 徐建闽, 刘正东. 基于卡尔曼滤波算法的公交车辆行程时间预测[J]. 交通运输研究, 2007, 000(002):174-177.
❤️ 关注我领取海量matlab电子书和数学建模资料
❤️部分理论引用网络文献,若有侵权联系博主删除























 287
287











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










