计算摄影中的图像恢复

最新推荐文章于 2025-04-11 15:06:09 发布

Matrix_11

最新推荐文章于 2025-04-11 15:06:09 发布

阅读量1k

点赞数 1

分类专栏：计算摄影与图像处理

本文链接：https://blog.csdn.net/matrix_space/article/details/104736315

版权

计算摄影与图像处理专栏收录该内容

98 篇文章

订阅专栏

最近几年，有一个研究方向随着手机拍照的崛起而受到了越来越多的关注，也就是 computation photograph，中文翻译过来就叫计算摄影，顾名思义，计算摄影，就是计算+摄影，因为手机受到各种硬件的约束和限制，和单反比，不可能有更大的镜头，更大的 sensor，更灵活的变焦系统，所以为了提升手机摄影的效果，就需要依赖更好的算法，这就是计算摄影的由来，各大厂商，都在硬件的基础上，深挖自己的算法能力，以便让手机摄影的效果更好，更真实。

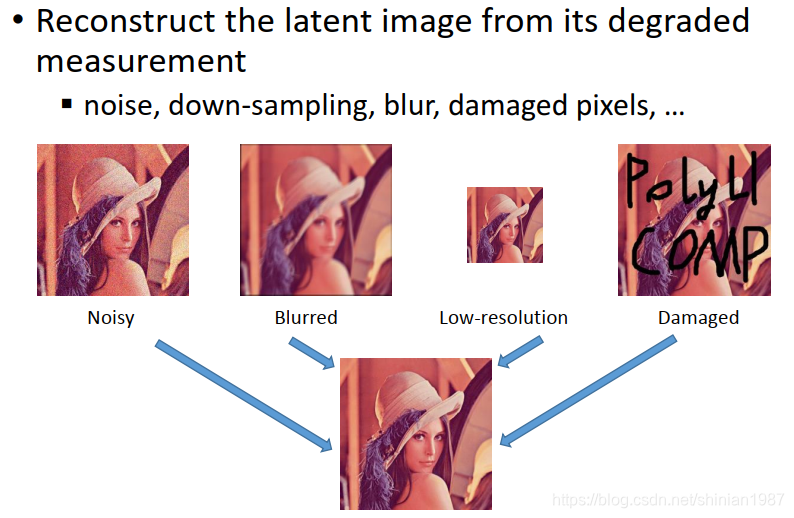
在计算摄影中，以一类问题是最常见的，也就是我们所说的图像恢复问题，我们知道虽然镜头结合sensor模拟的是人的视觉成像系统，但是与人眼的视觉成像相比，现在的硬件可能还达不到那么好的成像质量，所以一般情况下，sensor 捕获的信息，与人眼直接看到的信息相比，是存在一定的退化的，图像恢复算法，就是要把退化的图像质量提升，比如下图所示：

在这里插入图片描述

插入图片

常见的质量退化，比如噪声，模糊，低分辨率或者图像块的缺失等等。

在图像恢复模型中，我们一般会建立如下的成像模型：

$\mathbf{y} = \mathcal{T} \mathbf{x} + \mathbf{n}$

其中 $\mathbf{y}$ 是观测到的质量退化的图像， $\mathbf{x}$ 是我们想要恢复的图像， $\mathbf{n}$ 表示噪声， $\mathcal{T}$ 表示成像的退化过程，由于噪声，光照以及其它因素的干扰， $\mathbf{y}$ 的质量相比于 $\mathbf{x}$ 要下降很多，我们在已知 $\mathbf{y}$ 的情况下，要恢复出 $\mathbf{x}$ ，这是一个典型的逆问题，一般来说不存在一个精确的解析解，只能通过优化的方法求得近似解。

$\mathcal{T}$ 一般来说是一个很庞大的矩阵，如果我们能够估计出 $\mathcal{T}$ 的值或者说分布，那么我们就能恢复出 $\mathbf{x}$ ，不同的情况下， $\mathcal{T}$ 表示的含义不同，在噪声成像模型中， $\mathcal{T}$ 可以认为是一个单位矩阵，我们要做的就是把 $\mathbf{n}$ 去掉，在模糊成像中， $\mathcal{T}$ 可以看成是一个模糊核构成的矩阵，在低分辨率的情况下， $\mathcal{T}$ 可以认为是一个降采样矩阵再加一个模糊矩阵的乘积，如果是 inpainting 的情况，那么 $\mathcal{T}$ 就类似一个 0-1 构成的 mask。

一般求解这类问题的优化函数，都可以写成下面类似的方程：

$\mathbf{x}^* = \min_{\mathbf{x}} E(\mathbf{x}; \mathbf{y}) + R(\mathbf{x})$

$\mathbf{x}^*$ 就是我们想要求得的最优解， $E(\mathbf{x}; \mathbf{y})$ 表示和任务相关的一个优化函数，一般是一个能量函数， $R(\mathbf{x})$ 一般是约束项，或者称为先验项，要很好的解决图像恢复问题，需要满足三个条件：

构建一个好的成像模型
构造一个好的先验
构造一个好的目标函数

字典学习 Dictionary learning

在深度学习兴起之前，图像恢复问题一般都是基于一种稀疏表示的方法来解决，这种方法是把 $R(\mathbf{x})$ 用一个字典来表示，

$\mathbf{x} = D \alpha$

通过对 $\alpha$ 进行约束，可以将如下的优化目标函数：

$\min_{\mathbf{x}} || \mathcal{T} \mathbf{x} - \mathbf{y} ||_{2}^2 + R(\mathbf{x})$

转化成如下的形式：

$\min_{\mathbf{x}} || \mathcal{T} D \alpha - \mathbf{y} ||_2^2 + \lambda ||\alpha||_1$

这样，求解 $\mathbf{x}$ 就变成求解 $\alpha$ 了。

在实际的求解过程中，先将一张图像拆分成多个有 overlap 的 patch，然后对分别对每个 patch，用上面的优化表达式来求解 $\alpha$ ，求解出 $\alpha$ 之后，可以对某个 patch 进行重建：

$\hat{\mathbf{x}} = D \hat{\alpha}$

将重构的多个 patch 再拼成一幅完整的图像。一般来说，我们希望 $\alpha$ 是稀疏的，而字典 $D$ 则是 over complete，如果我们将 $\mathbf{x}$ 看成是一个列向量， $D$ 看成是一个矩阵，每一列可以看成是与 $\mathbf{x}$ 相似的向量， $\alpha$ 则表示矩阵 $D$ 的列向量的系数，这样表示的好处，就是我们可以通过学习一个字典，表示很多不同的 patch，假设 $\mathbf{x}$ 是一个 N 维的列向量， $\alpha$ 是一个 $K$ 维的列向量， $D$ 是一个 $\times D$ 的矩阵，如果 $ K << N$，也就是说如果 $K$ 远远小于 $N$ 那么我们就可以认为 $\alpha$ 是一个稀疏的表示，因为 $D$ 是公用的，而 $\alpha$ 是和当前要求的 $\mathbf{x}$ 相关的，稀疏表示，可以让模型用少量的 $\alpha$ 去重构一个 patch，为了让 $\alpha$ 稀疏，意味着字典 $D$ 的表达能力要足够强，理想情况下，最好字典只用几个列向量的组合，就可以重构出 $\mathbf{x}$ ，为了提升字典 $D$ 的表达能力，一般都是通过字典学习的方法来构建字典。

除了字典学习，Low-rank minimization 也是图像恢复中比较常用的一种方法，一幅好的自然图像如果看成矩阵的话，一般来说都是低秩的，因为自然图像里的结构信息有很大的冗余和相关性，

低秩与稀疏：低秩是指矩阵的秩较小，稀疏是指矩阵中非零元素的个数少。如果对矩阵进行奇异值分解，并把其所有奇异值排列为一个向量，那么这个向量的稀疏性便对应于该矩阵的低秩性。

Deep learing 与图像恢复

随着深度学习的流行，图像恢复领域也开始越来越多的结合深度学习来实现图像恢复，基于深度学习的图像恢复，就是通过大量的训练样本对学习一个紧凑的映射函数，

$min_{\Theta} L(\hat{x}, x) \quad s.t. \quad \hat{x} = F(y, H, \Theta)$

$\hat{x}, x$ 可以看成是训练数据对，分别对应网络的输入，输出
$F$ 可以看成是函数形式，或者说神经网络的结构
$\Theta$ 表示函数的参数，或者说神经网络的参数
$L$ 表示loss 函数

基于深度学习的图像恢复流程一般如下图所示：

在这里插入图片描述

插入图片

训练的过程包括构造训练数据，设计网络结构，设计 loss 函数，调试模型，进行训练

深度学习的图像恢复，就是通过大数据，让模型自己去学习大量图像的纹理结构，基于深度学习的图像恢复现在已经越来越成为主流方法了，目前各个榜单上，最好的性能都是基于深度学习的方法来实现的。

实现形式也多种多样，从一开始的普通多层卷积，到后来的 residual block 架构，再到后来融入 GAN 模型，loss 的设计也越来越精细，一开始只考虑最小均方误差，后来融入了 perceptual loss，以及 GAN loss。

虽然基于深度学习的图像恢复方法层出不穷，不过基于学习的图像恢复，最关键的一个问题就是训练数据的构建，特别是针对真实场景的图像恢复，目前学术界，构建训练数据的方式主要还是仿真，模拟图像退化的过程，但是真实场景的图像退化非常复杂，大多数情况下，只能拿到低质量的图像，而高质量的图像一般是不存在的，所以对于真实场景来说，如何构建训练数据，是深度学习能否有效的关键。