统计学习三要素
李航博士在《统计学习方法》一书中这样描述统计学习方法的构成:
方法=模型+策略+算法
本人更形象地借助产品经理的视角可以类比这样的:
方法=设想+指标+方案
下面就具体学习这三个要素(三要素是宏观上处理问题的一种框架):
模型
统计学习首先要考虑的问题是学习什么样的模型。以监督学习为例,模型就是说要学习的条件概率分布或决策函数。模型的假设空间(hypothesis space)包含所有可能的条件概率分布或决策函数(其实就是他们的集合)。通常该函数的集合是由一个参数向量决定的函数簇。参数向量取值于N维欧式空间,就称为参数空间(parameter space)。
策略
这一步需要考虑的是按照什么样的准则学习或选择最优的模型(当然是从假设空间中选择了)。这里要介绍几个用到的概念:
损失函数(loss function)
损失函数度量模型一次预测的好坏,度量预测值f(X)和真实值Y之间的错误程度,是非负实值函数,可以记作:L(Y,f(X))。常用的比如:
平方损失函数: L(Y,f(X))=1/2 * (Y-f(X))^2
对数损失函数: L(Y,f(X)) = -logP(Y|X)
风险函数(risk function)
风险函数度量的是平均意义下的模型预测的好坏。损失函数值越小,模型就越好。输入输出(X,Y)是随机变量,遵循联合分布P(X,Y),所以损失函数的期望是:
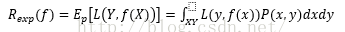
这是理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失,称为风险函数或期望损失。学习的目标就是选择期望风险最小的模型。
给定一个训练数据集:
经验风险或经验损失记作:
经验风险是模型关于训练样本集的平均损失。根据大数定律,当样本容量N越来越大时,经验风险越趋近于期望风险。所以就可以用经验风险去估计期望风险,但是在样本不足的情况下,往往不够理想,需要对经验风险进行矫正,见下。
经验风险最小化(empirical risk minimization,ERM)
该策略认为经验风险最小的模型就是最优的模型,见下:
当样本容量足够大时,经验风险最小化能得到很好的学习效果。举例:极大似然估计。但是样本容量较小时会产生“过拟合”现象。
结构风险最小化(structural risk minimization,SRM)
结构风险最小化就是为了防止过拟合的策略,等价于正则化(regularization),就是在经验风险最小化上加上表示模型复杂度的正则化项或惩罚项,如下:
其中J(f)是模型复杂度,模型f越复杂,J(f)就越大,反之f越简单,J(f)就越小。(举例:贝叶斯估计中的最大后验概率估计),这时,结构风险最小的模型就是最好的模型。
算法
算法就是根据学习策略,从假设空间中选择最优的模型的计算方法。往往这个时候就将问题转化为最优化问题。通常问题的解析解不存在,需要用数值计算的方法求解,如何保证找到全局最优解就是个重要问题。
总结
这里本人主要是摘取《统计学习方法》书中的有关内容,稍加整理而成。其实该部分内容看上去很“软”,不算是有什么干货,但是本人在第二遍阅读的时候,有种突然顿悟的感觉,宏观上明白了机器学习的流程和目的,本质上更认为这是一个大的指导框架,对今后学习有一定的帮助。
参考资料:
《统计学习方法》李航 著








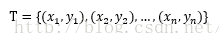
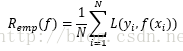
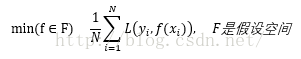
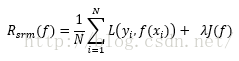
















 815
815

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








