（CV，Math）仿射几何

本文地址：http://blog.csdn.net/mounty_fsc/article/details/51492927

本文简单介绍了仿射变换，主要从仿射变换的矩阵表示方面理解。

1 仿射变换矩阵表示

以二维坐标为例讲述仿射变换。变换前坐标为$(x,y)$，变换后坐标为$(x',y')$，本文均使用齐次坐标系，齐次坐标见《射影变换》。

二维仿射变换保持了图像的“平直性”（即变换后直线还是直线）和“平行性”（平行线还是平行线）。仿射变换可以通过一系列的原子变换的复合来实现，包括：平移（Translation）、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切（Shear）。其中平移与旋转为刚体变换，平移、旋转与缩放为相似变换。

仿射变换用等式表示如下：

$$\begin{equation} \left\{ \begin{aligned} x'=ax+cy+tx\\ y'=bx+dy+ty \end{aligned} \right. \end{equation}$$

用矩阵表示如下：

$$\left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right)= \left( \begin{array}{ccc} a & c & tx \\ d & b & ty \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right)$$

1.1 平移Translation

$(x,y)$平移后坐标为$(x+tx,y+ty)$，变换矩阵为

$$\left( \begin{array}{ccc} 1 & 0 & tx \\ 0 & 1 & ty \\ 0 & 0 & 1 \end{array} \right)$$

1.2 缩放Scale

$(x,y)$缩放后坐标为$(ax,dy)$，变换矩阵为

$$\left( \begin{array}{ccc} sx & 0 & 0 \\ 0 & sy & 0 \\ 0 & 0 & 1 \end{array} \right)$$

1.3 翻转Flip

$(x,y)$翻转后坐标为$(-x,y)$或$(x,-y)$，变换矩阵为

$$\left( \begin{array}{ccc} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)或 \left( \begin{array}{ccc} 1& 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{array} \right)$$

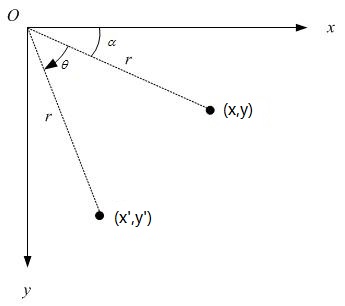
1.4 旋转Rotation

$(x,y)$旋转后坐标为$(xcos\theta -ysin\theta,ycos\theta+xsin\theta)$，变换矩阵为

$$\left( \begin{array}{ccc} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{array} \right)$$

$$\begin{equation} \left \{ \begin{aligned} & x=rcos\alpha \\ & y=rsin\alpha \\ & x'=rcos(\alpha+\theta)=rcos\alpha cos\theta-rsin\alpha sin\theta =xcos\theta -ysin\theta \\ & y'=rsin(\alpha+\theta)=rsin\alpha cos\theta+rcos\alpha sin\theta=ycos\theta+xsin\theta \end{aligned} \right. \end{equation}$$

注，若围绕某点$(x_0,y_0)$旋转，则可以理解为坐标系平移$(x_0,y_0)$后再进行旋转，即对$(x-x_0,y-y_0)$旋转后得到$(x'-x_0,y'-y_0)$

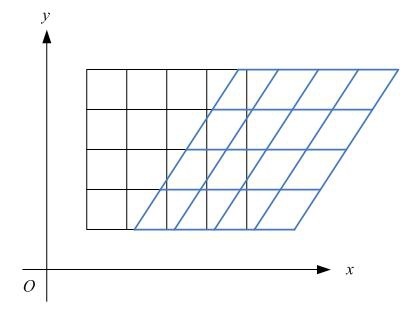
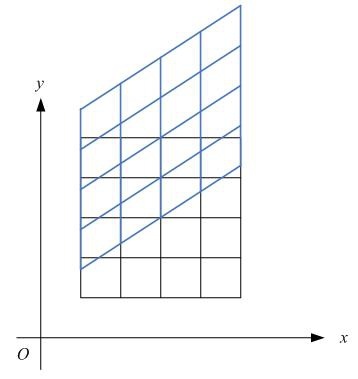
1.5 剪切Shear

$(x,y)$剪切后坐标为$(x+cy,y+bx)$，变换矩阵为

$$\left( \begin{array}{ccc} 1 & shx & 0 \\ shy & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)$$
也相当于水平剪切和垂直剪切的符合：
$$\left( \begin{array}{ccc} 1 & 0 & 0 \\ shy' & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 1 & shx' & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)$$
水平、垂直剪切如下图

1.6 刚体变换

由上可知，刚体变换包括平移和旋转，所以变换矩阵可以表示为，其中$R$为3*3的正交旋转矩阵

$$\left( \begin{array}{cc} R & t \\ 0^T & 1 \end{array} \right)$$

1.7 总结

1. 从以上可以看出，若某物质或信息具有仿射不变性，则也具备尺度不变性（Scale invariant)

2 仿射几何

这部分描述的仿射几何的一些重要的数学概念。

2.1 平行射影

又称透视仿射，是射影几何的概念，由此可知仿射变换是射影变换的一种特例。

平面到平面的仿射是有限回平行射影的积组成的。比如，由连续施行平面$\pi$到$\pi1$，$\pi1$ 到$\pi2$，$\pi2$到$\pi3$，再从$\pi3$回到$\pi'$的共四次平行投影得到的平面$\pi$上点之间的对应，例如$A，B，C$的对应点为$A′，B′，C′$，这个对应就是平面π上的一个仿射变换。

2.2 简比

• 定义$\frac{AC}{BC}$为三共线点$A，B，C$的简比
• 简比在仿射变换下是不变的，即$\frac{AC}{BC}=\frac{A'C'}{B'C'}$
• 简比是仿射变换最基本的不变量

参考资源：
1. http://blog.csdn.net/kesalin/article/details/577973
2. http://liuyanwei.jumppo.com/2015/11/24/iOS-affine-transfermation-animation.html?utm_source=tuicool&utm_medium=referral
3. http://www.th7.cn/Program/Android/201501/353476.shtml
4. http://www.360doc.com/content/14/0410/14/10724725_367760675.shtml