本文地址:http://blog.csdn.net/mounty_fsc/article/details/51496640
计算机视觉中常涉及欧式几何(Euclidean Geometry)、仿射几何(Affine Geometry)、射影几何(Projective Geometry)、微分几何( Differential Geometry)。
1 射影空间
对
n
维欧式空间加入无穷远元素,并对有限元素和无穷远元素不加区分,则他们共同构成
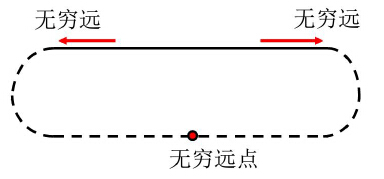
一维射影空间是一条射影直线,由欧氏直线和它的无穷远点构成
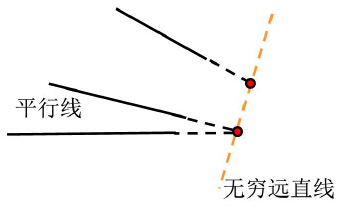
二维射影空间是一个射影平面,由欧氏平面和它的无穷远直线构成
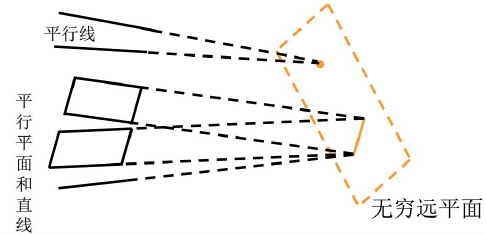
三维射影空间由我们所在的空间和无穷远平面构成
2 齐次坐标系
2.1 为什么需要齐次坐标
在欧氏空间中建立坐标系后,便有了点与坐标间的一一对应。但当引入无穷点以后,无穷远点无坐标,为了刻化无穷远点的坐标,我们引入齐次坐标。
2.2 定义
- 用 n+1 维向量表示 n 维向量。
- 设
n 维空间的非齐次坐标为 (x′1,…,x′n) ,即为 n 维欧式空间坐标 - 则
n 维空间的齐次坐标为 (x1,…,xn,x0) ,其中 x0 称为哑坐标 - x0=0 时,表示的点为无穷远点
2.3 转换关系
x0≠0 时, x′1⋅x0=x1,…,x′n⋅x0=xn
2.4 直线与平面的表示
- 二维空间的直线
非齐次坐标: ax1+bx2+c=0
齐次坐标: ax1+bx2+cx0=0
无穷远直线方程: x0=0 - 三维空间的平面
非齐次坐标: ax1+bx2+cx3+d=0
齐次坐标: ax1+bx2+cx3+dx0=0
无穷远平面方程: x0=0
2.5 注意
- x0 的取值是不唯一的,所以一个点的齐次坐标是不唯一的。即非齐次坐标与其次坐标是“一对多”的关系
- 当 x0=1 时齐次坐标为规格化齐次坐标
3 射影不变量
射影不变量包括交比、线束交比、简比。
3.1 交比(cross ratio)
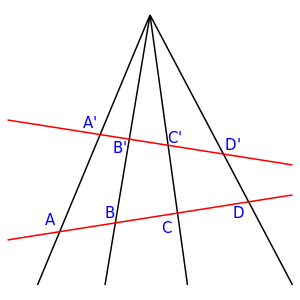
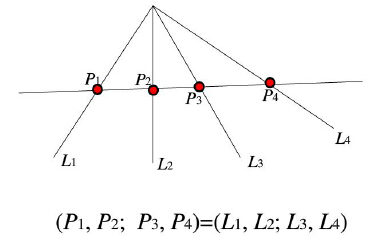
定义共线四点 A,B,C,D 交比如下:
(A,B;C,D)=ACBC:ADBD=AC⋅BDBC⋅AD射影变换下交比不变,则
- 交比还可以通过定义仿射坐标系,通过代数的方式来定义,此处略
3.2 线束交比
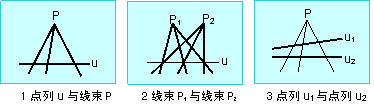
3.1的交比针对点列,点列与线束的概念如图可以反应:
线束交比由射影平面偶像性质得来。即“点”与“直线”为对偶元素,“过一点作一条直线”与“在一条直线上取一点”为对偶作图
共线的四个点有交比,根据对偶,共点的四条线也有交比。且有对应的四点与四线的交比相等,如图等式。
3.3 简比
简比已在(CV,Math)仿射几何中介绍了。
3.4 三者关系
- 简比 SR(A,B;C)=ACBC
- 交比 CR(A,B;C,D)=SR(A,B;C)SR(A,B;D)=ACBC:ADBD
- 线束交比 CR(l1,l2;l3,l4)=sin(l1,l3)sin(l2,l3):sin(l1,l4)sin(l2,l4)
4 射影变换
4.1 定义
记
Sn,S′n
是两个由点组成的射影空间。
T
是由
- 点和直线的结合关系。即共线三点仍然共线。
- 共线的四个点的交比不变。
则
此外,有定理:
保持点列的交比不变是射影变换的充分必要条件
4.2 矩阵表达
n
维射影空间可用如下等式表达射影变换:
其中 ρ 为标量比例因子, x,y 为变换前与变换后齐次坐标。射影变换用 (n+1)×(n+1) 维矩阵 M 表示,如下:
若
M
的行列式非零,则
4.3 其他问题
- 由射影变换可由矩阵表示看知,齐次坐标下,射影变换是线性的。但非齐次坐标下,射影变换是非线性。
- 射影变换由矩阵
M
确定,
M 共有参数 (n+1)2 个。但 M 与kM 表示同一变换(因等式两边都是齐次坐标表示不唯一),故 M 的独立参数为(n+1)2−1
4 射影、仿射、欧式空间关系
4.1 仿射变换与射影变换
- 仿射变换为射影变换特例,此时假设中心投影射线平行。仿射变换矩阵与射影变换矩阵也反应了这个问题,以二维空间为例,仿射变换与射影变换的矩阵的一般形式分别为
- 在射影几何中已证明,如果射影变换使无穷远点仍变换为无穷远点,则变换为仿射变换,以二维变换为例,若
x
为无穷远点,则坐标为
(x1,x2,0) ,仿射变换后点 y 坐标为(y1,y1,0) ,则有:
ρ⎛⎝⎜y1y20⎞⎠⎟=⎛⎝⎜m11m21m31m12m22m32m13m23m33⎞⎠⎟⎛⎝⎜x1x20⎞⎠⎟
所以有 m31=0,m32=0
4.2 不变量
- 射影变换保持直线,直线与点的接合性以及直线上点列的交比不变
- 仿射变换除具有以上不变性外,还保持直线与直线的平行性、直线上点列的简比不变
- 欧氏变换除具有仿射变换的不变性外,还保持两条相交直线的夹角不变,任意两点的距离不变
参考资料:




























 485
485

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








