Probabilistic Machine Learning：Introduction 概率机器学习：简介- 2 概率：一元模型（2）-page 75-79 /858

2.3 贝叶斯定理
贝叶斯定理对于概率理论的意义，类似于毕达哥拉斯定理在几何学中的地位。
— 哈罗德·杰弗里斯爵士，1973年[Jef73]。
在本节中，我们讨论贝叶斯推断的基础知识。根据韦氏词典的定义，术语“推断”指的是“从样本数据到一般性结论的过程，通常伴随着计算出的确定度”。术语“贝叶斯”用于指代使用概率论表示“确定度”的推断方法，它利用贝叶斯定理7来根据数据更新确定度。
贝叶斯定理本身非常简单：它只是一个用于计算未知（或隐藏）量H可能值的概率分布的公式，给定一些观察到的数据Y = y：
[ p(H = h|Y = y) = \frac{p(H = h)p(Y = y|H = h)}{p(Y = y)} ] (2.51)
这自然地推导自等式
[ p(h|y)p(y) = p(h)p(y|h) = p(h, y) ] (2.52)
这本身是从概率的乘法规则得出的。
在公式(2.51)中，术语p(H)表示我们在看到任何数据之前对H可能值的了解；这被称为先验分布。（如果H有K个可能的值，则p(H)是一个K个概率的向量，它们总和为1。）术语p(Y |H = h)表示在H = h的情况下我们预期看到的可能结果Y的分布；这被称为观察分布。
当我们在对应于实际观察的点评估这一点时，得到的函数是[ p(Y = y|H = h) ]，称为似然函数。（请注意，这是h的函数，因为y是固定的，但它不是概率分布，因为它不总和为1。）将先验分布[ p(H = h) ]乘以每个h的似然函数[ p(Y = y|H = h) ]会得到未归一化的联合分布[ p(H = h, Y = y) ]。我们可以通过除以[ p(Y = y) ]将其转换为规范化分布，称为边际似然，因为它通过边缘化未知的H计算：
[ p(Y = y) = \sum_{h_0 \in H} p(H = h_0)p(Y = y|H = h_0) = \sum_{h_0 \in H} p(H = h_0, Y = y) ] (2.53)

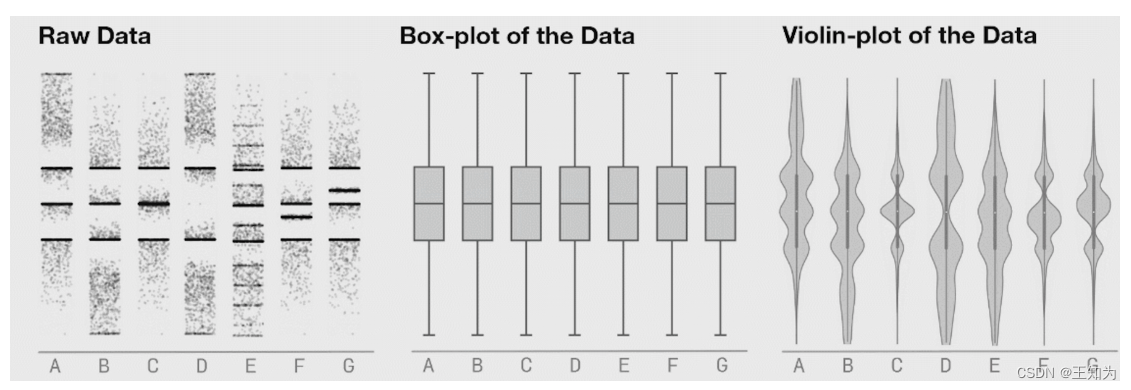
图2.7：7个不同数据集的插图（左侧），相应的箱线图（中间），和小提琴箱线图（右侧）。来自https://www.autodesk.com/research/publications/same-stats-different-graphs的第8图。在Justin Matejka的友善许可下使用。

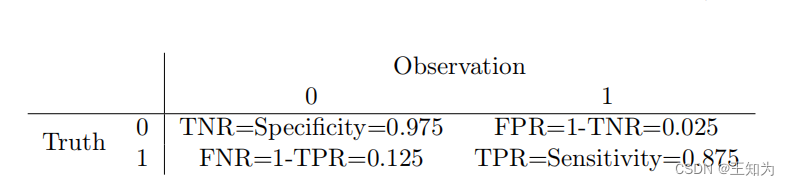
表2.1：给定两种可能的隐藏状态H，二元观察Y的似然函数p(Y |H)。每行总和为1。缩写：TNR为真负率，TPR为真正率，FNR为假负率，FPR为假正率。

通过计算每个h的[ \frac{p(H = h, Y = y)}{p(Y = y)} ]来对联合分布进行归一化，得到后验分布[ p(H = h|Y = y) ]；这表示我们关于H可能值的新信念状态。

我们可以用文字总结贝叶斯定理如下：
[ \text{后验} \propto \text{先验} \times \text{似然} ] (2.54)

在这里，我们使用符号[ \propto ]表示“与之成比例”，因为我们忽略了分母，它只是与H无关的一个常数。使用贝叶斯定理根据相关观察到的数据更新关于某个感兴趣的数量的未知值的分布称为贝叶斯推断或后验推断。它也可以简称为概率推断。

以下是一些贝叶斯推断实际应用的简单例子。在本书后面，我们将看到更多有趣的例子。

2.3.1 例子：COVID-19检测
假设你认为自己可能感染了COVID-19，这是一种由SARS-CoV-2病毒引起的传染病。你决定进行诊断测试，并希望使用测试结果来确定是否感染。
令H = 1表示你感染的事件，H = 0表示你没有感染的事件。令Y = 1表示测试为阳性，Y = 0表示测试为阴性。我们想要计算[ p(H = h|Y = y) ]，其中h ∈ {0, 1}，其中y是观察到的测试结果。（为简洁起见，我们将值的分布[ p(H = 0|Y = y), p(H = 1|Y = y)] ]写为[ p(H|y) )。我们可以将其视为二元分类的一种形式，其中H是未知的类标签，而y是特征向量。
首先，我们必须指定似然函数。这个量显然取决于测试的可靠性。有两个关键参数。灵敏度（也称为真正率）定义为[ p(Y = 1|H = 1) ]，即在事实为正时测试为阳性的概率。假阴性率定义为灵敏度的补数。特异性（也称为真负率）定义为[ p(Y = 0|H = 0) ]，即在事实为负时测试为阴性的概率。假阳性率定义为特异性的补数。我们在表2.1中总结了所有这些数量。（有关更多详细信息，请参见第5.1.3.1节。）根据https://nyti.ms/31MTZgV，我们将灵敏度设置为87.5%，将特异性设置为97.5%。
接下来，我们必须指定先验分布。量[ p(H = 1) ]表示你所在地区的疾病患病率。我们将其设置为[ p(H = 1) = 0.1 ]（即10%），这是2020年春季纽约市的患病率。（选择这个例子是为了与https://nyti.ms/31MTZgV中的数字相匹配。）

现在假设你的检测结果为阳性。我们有：

[ p(H = 1|Y = 1) = \frac{p(Y = 1|H = 1)p(H = 1)}{p(Y = 1|H = 1)p(H = 1) + p(Y = 1|H = 0)p(H = 0)} ] (2.55)

[ = \frac{TPR \times prior}{TPR \times prior + FPR \times (1 - prior)} ] (2.56)

[ = \frac{0.875 \times 0.1}{0.875 \times 0.1 + 0.025 \times 0.9} = 0.795 ] (2.57)

因此，你被感染的概率为79.5%。

现在假设你的检测结果为阴性。你被感染的概率由以下公式给出：

[ p(H = 1|Y = 0) = \frac{p(Y = 0|H = 1)p(H = 1)}{p(Y = 0|H = 1)p(H = 1) + p(Y = 0|H = 0)p(H = 0)} ] (2.58)

[ = \frac{FNR \times prior}{FNR \times prior + TNR \times (1 - prior)} ] (2.59)

[ = \frac{0.125 \times 0.1}{0.125 \times 0.1 + 0.975 \times 0.9} = 0.014 ] (2.60)

因此，你被感染的概率只有1.4%。

如今，COVID-19的患病率要低得多。假设我们使用1%的基础患病率重复这些计算，现在后验概率分别减少到26%和0.13%。

事实上，即使在阳性测试后，你只有26%的概率感染COVID-19，这是非常反直觉的。原因是单个阳性测试更可能是误报，而不是由于疾病引起，因为该疾病是罕见的。为了看清楚这一点，假设我们有一个人口，其中有100,000人，其中有1,000人感染。其中感染者中，875 = 0.875 × 1000测试结果为阳性；而在未感染者中，2475 = 0.025 × 99,000测试结果为阳性。因此，阳性的总数是3350 = 875 + 2475，因此在阳性测试结果下感染的后验概率为875/3350 = 0.26。

当然，上述计算假设我们知道测试的灵敏度和特异度。有关在这些参数存在不确定性时如何应用贝叶斯规则的详细信息，请参阅[GC20]。

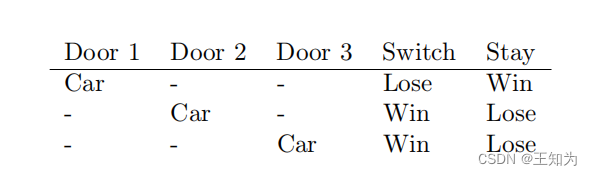
表2.2：蒙提霍尔游戏的3种可能状态，表明与坚持最初选择相比，换门平均而言更好。改编自[PM18]的表6.1。

从直觉上看，似乎不应该有任何区别，因为你最初选择的门不能影响奖品的位置。然而，主持人打开门3的事实告诉我们有关奖品位置的一些信息，因为他在知道真实位置和你的选择的条件下进行了选择。正如下文所示，事实上，如果你切换到门2，你获胜的概率将是坚持选择门1的两倍。

为了证明这一点，我们将使用贝叶斯定理。让(H_i)表示奖品在门(i)后面的假设。

我们做出以下假设：三个假设(H1)、(H2)和(H3)在先验上是等可能的，即
[ P(H1) = P(H2) = P(H3) = \frac{1}{3} ] (2.61)

在选择门1后，我们收到的数据要么是(Y = 3)，要么是(Y = 2)（分别表示打开门3或门2）。我们假设这两种可能的结果具有以下概率。如果奖品在门1后面，那么主持人在(Y = 2)和(Y = 3)之间随机选择。否则主持人的选择是强制性的，概率分别为0和1。
[ P(Y = 2|H1) = \frac{1}{2} \quad P(Y = 2|H2) = 0 \quad P(Y = 2|H3) = 1 ]
[ P(Y = 3|H1) = \frac{1}{2} \quad P(Y = 3|H2) = 1 \quad P(Y = 3|H3) = 0 ] (2.62)

现在，使用贝叶斯定理，我们评估假设的后验概率：
[ P(H_i|Y = 3) = \frac{P(Y = 3|H_i)P(H_i)}{P(Y = 3)} ] (2.63)

[ P(H1|Y = 3) = \frac{\frac{1}{2} \times \frac{1}{3}}{P(Y =3)} \quad P(H2|Y = 3) = \frac{1 \times \frac{1}{3}}{P(Y =3)} \quad P(H3|Y = 3) = \frac{0 \times \frac{1}{3}}{P(Y =3)} ] (2.64)

分母[ P(Y = 3) ]是[ P(Y = 3) = \frac{1}{6} + \frac{1}{3} = \frac{1}{2} ]。所以
[ P(H1|Y = 3) = \frac{1}{3} \quad P(H2|Y = 3) = \frac{2}{3} \quad P(H3|Y = 3) = 0 ] (2.65)

因此，参赛者应该切换到门2以获得获奖的最大机会。请参见表2.2以获取详细示例。

许多人发现这个结果令人惊讶。使其更加直观的一种方法是进行一个思想实验，在这个游戏中有一百万扇门。现在的规则是，参赛者选择一扇门，然后游戏主持人以不透露奖品的方式打开999,998扇门，留下参赛者选择的门和另一扇门仍然关闭。参赛者现在可以坚持或切换。想象一下，面对一百万扇门的参赛者，其中门1和门234,598没有被打开，门1是参赛者的初次猜测。你认为奖品在哪里？