策略迭代与值迭代都属于强化学习里面策略求解中的动态规划方法。其区别是什么呢?
首先看一张图片:
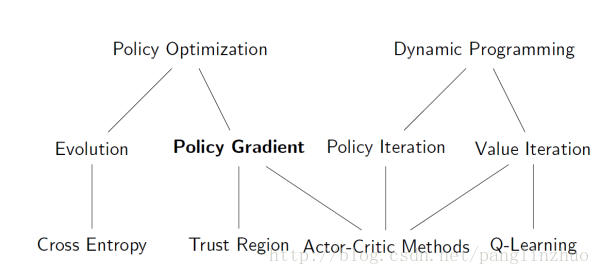
首先看策略迭代:

1.initialization
初始化所有状态的v(s)以及π(s)(初始化为随机策略)
2.poicy evaluation
用当前的v(s)对当前策略进行评估,计算出每一个状态的v(s),直到v(s)收敛,才算训练好了这个状态价值函数V(s)
3.policy improvement
既然上一步已经得到了当前策略的评估函数V(s),那么就可以利用这个评估函数进行策略改进啦。
在每个状态s时,对每个可能的动作a,都计算一下采取这个动作后到达的下一个状态的期望价值。看看哪个动作可以到达的状态的期望价值函数最大,就选取这个动作。以此更新了π(s)
然后再次循环上述2、3步骤,直到V(s)与π(s)都收敛。
正如下面所说:
In Policy Iteration algorithms, you start with a random policy, then find the value function of that policy (policy evaluation step), then find an new (improved) policy based on the previous value function, and so on. In this process, each policy is guaranteed to be a strict improvement over the previous one (unless it is already optimal). Given a policy, its value function can be obtained using the Bellman operator.
再来看值迭代:
1.initialization
初始化所有状态的v(s)
2.finding optimal value function(找到最优的价值函数)
注意伪代码里的max,对每一个当前状态s,对每个可能的动作a,都计算一下采取这个动作后到达的下一个状态的期望价值。看看哪个动作可以到达的状态的期望价值函数最大,就将这个最大的期望价值函数作为当前状态的价值函数v(s) 循环执行这个步骤,直到价值函数收敛,就可以得到最优optimal的价值函数了
3.policy extraction
利用上面步骤得到的optimal价值函数和状态转移概率,就计算出每个状态应该采取的optimal动作,这个是deterministic呦。
In Value Iteration, you start with a randon value function and then find a new (improved) value function in a iterative process, until reaching the optimal value function. Notice that you can derive easily the optimal policy from the optimal value function. This process is based on the Optimality Bellman operator.
区别及联系
1.策略迭代的第二步policy evaluation与值迭代的第二步finding optimal value function十分相似,除了后者用了max操作,前者没有max.因此后者可以得出optimal value function, 而前者不能得到optimal function.
2.策略迭代的收敛速度更快一些,在状态空间较小时,最好选用策略迭代方法。当状态空间较大时,值迭代的计算量更小一些。






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








