伺服控制的补偿算法

最新推荐文章于 2025-02-14 09:48:59 发布

是纯一呀

最新推荐文章于 2025-02-14 09:48:59 发布

阅读量3.3k

点赞数 29

分类专栏：ＰＩＤ文章标签：算法嵌入式硬件 python

本文链接：https://blog.csdn.net/pillpeople/article/details/141993512

版权

ＰＩＤ专栏收录该内容

1 篇文章

订阅专栏

什么是伺服控制？

伺服控制是一种闭环控制系统，主要用于精确控制物体的位置、速度和加速度等运动参数。它广泛应用于自动化设备中，比如数控机床、机器人、无人机和工业自动化设备。

伺服控制系统通常由以下几个部分组成：

伺服电机：用于驱动机械部件。
传感器：监控实际位置、速度或加速度，并将信号反馈给控制器。
控制器：根据设定的目标（如期望的位置或速度）和传感器反馈的数据，生成适当的控制信号，调节伺服电机的动作。
反馈环路：控制器通过反馈环路不断调整系统，确保实际输出接近设定目标。

简单来说，伺服控制通过控制电机来精确调整物体的运动，并通过传感器反馈来不断修正误差，最终实现高精度的控制。

为什么伺服控制需要补偿算法？

伺服控制需要补偿算法是为了提升系统的精度、稳定性和响应速度。

1. 系统误差的存在

稳态误差：在系统达到稳态时，实际输出和设定目标之间可能仍存在差距，这就是所谓的稳态误差。为了消除这种误差，常需要通过补偿算法进行调节。

2. 系统延迟与动态响应

伺服系统通常存在一定的动态延迟，可能导致系统在响应设定目标时出现滞后或者超调现象。通过补偿算法，可以提前预测和调节系统的输出，提升动态响应性能。

3. 外界干扰

伺服系统在实际应用中会受到来自外部的干扰（如摩擦力、负载变化、环境因素等），这些干扰可能影响系统的性能。补偿算法能够帮助系统在干扰发生前或发生时进行自我调节，抵消干扰对控制的影响。

4. 模型不确定性

伺服控制系统中的一些参数（如电机惯量、阻尼等）可能会因为环境或负载变化而有所不同。为了使控制系统在各种情况下都能表现出理想的性能，补偿算法可以根据实际情况动态调整系统参数，确保系统能够适应变化。

5. 系统非线性

伺服系统中的一些非线性因素（如摩擦力、齿隙等）会影响系统的精度。通过设计合适的补偿算法，能够有效减小这些非线性因素对系统的影响，提升系统的控制精度和稳定性。

示例：自动门的伺服控制系统

有一个自动门，它的目标是能够根据人们的接近自动开关，并且在开关过程中保持平稳和精确的动作。我们通过一个伺服控制系统来实现这个功能。

1. 系统目标

目标位置：门要在有人接近时打开，并在无人时关闭到设定的初始位置。
目标速度：门需要在合理的时间内平稳且快速地开关，不应过快或过慢。

2. 伺服控制系统组成

伺服电机：用于驱动自动门的开关动作。通过控制电机的旋转方向和速度，能够精确地控制门的开关过程。
位置传感器：用于监测自动门当前的位置，反馈给控制器。
控制器：根据传感器的反馈和设定的目标位置，计算出需要的电机控制信号，控制伺服电机开门或关门。
反馈环路：控制器不断接收传感器的数据，实时调整电机的转速或方向，以确保门达到目标位置。

3. 工作流程

当有人靠近自动门时，感应器检测到信号，控制器将目标设定为“门需要完全打开”，即设定目标位置为“门完全打开的角度”。
控制器开始根据当前门的位置（通过位置传感器反馈）和设定的目标位置之间的误差，发出控制信号给伺服电机，让门逐渐打开。伺服电机根据控制器发出的指令，开始转动并推动门开启。
在门开启过程中，控制器不断接收位置传感器的反馈，并计算门当前的位置。如果门离目标位置（完全打开）还有一段距离，控制器继续发出指令让电机转动，直到误差减小到接近零。
当门完全打开后，伺服电机会停止转动。
如果人走开后，控制器接收到关闭门的指令，目标位置变为“门完全关闭的角度”，伺服系统重新驱动电机将门关闭。

4. 补偿算法在此的作用

速度控制：为了避免门在开关过程中速度过快或过慢，PID控制器可以调整电机的转速。例如，当门接近目标位置时，PID控制器中的比例和微分部分会让电机逐渐减速，避免快速关闭时的撞击。
误差补偿：如果在门关闭时出现了风吹等外部干扰，伺服控制系统通过传感器检测到门未完全关闭的误差，控制器会立刻发出额外的控制信号，抵消干扰，让门能够精确关闭到设定位置。
前馈控制：如果门的设计要求它必须在较快的时间内开关，那么控制器可以使用前馈控制算法，在人接近时立即发送适当的信号，提前推动门开始打开，减少响应时间。

几种常见的补偿算法：

1. PID控制（比例-积分-微分控制）

PID控制器是伺服系统中最经典和常用的补偿算法之一，分为三个部分：

P（比例控制）：根据当前误差来提供一个与误差成比例的控制信号，响应快，但会有稳态误差。
I（积分控制）：对误差进行累积，通过积分消除稳态误差，但可能引入超调。
D（微分控制）：根据误差变化率调节系统响应，减小系统震荡和超调。

应用：PID控制非常适合用于伺服电机的速度和位置控制，具有良好的动态响应和稳定性。

2. 前馈控制

前馈控制是一种基于系统模型的补偿算法，直接对控制输入施加影响，不依赖于反馈误差。前馈控制通过预测系统行为来提前补偿外界干扰，减少滞后。

应用：前馈控制通常与反馈控制结合使用，用于补偿已知的外部干扰或运动指令变化。例如，控制伺服电机的速度时，可以根据期望的加速度提前给出额外的电机驱动信号。

3. 最优控制（LQR - 线性二次调节器）

最优控制是通过设定系统的加权目标，找到控制信号的最优解，通常用于状态空间模型。LQR通过最小化误差和控制能量消耗，使系统在多个状态变量之间取得平衡。

应用：最优控制在多变量伺服系统中非常有效，适合复杂系统的精确控制，特别是在需要同时控制多个参数（如位置、速度和加速度）的场合。

4. 自适应控制

自适应控制能够根据系统的运行状态自动调整控制器参数。它对系统的模型不确定性和参数变化具有较好的适应能力。

应用：自适应控制适合那些参数随时间变化的伺服系统，比如负载变化较大的机器人控制系统。它可以在系统运行过程中动态调整控制参数，保证性能稳定。

5. 滑模控制

滑模控制是一种非线性控制方法，能够在系统不确定性较大的情况下，依然保持较好的鲁棒性。它通过设计滑模面，使系统状态沿着滑模面滑动，直到达到平衡点。

应用：滑模控制在应对大范围扰动和强烈干扰的伺服系统中表现出色。它广泛应用于高精度运动控制系统，如机器人手臂和高端工业机械。

6. 前馈-反馈复合控制

前馈-反馈复合控制结合了前馈和反馈控制的优点：

前馈控制：用来提前补偿已知的外部干扰或运动命令，提升系统的响应速度。
反馈控制：用于实时校正系统误差，确保系统的稳定性和精度。

应用：广泛应用于需要快速响应和高精度的伺服系统中，如CNC机床和高精度机器人系统。通过这种复合控制方式，系统能够快速响应并有效减少稳态误差。

7. 鲁棒控制

鲁棒控制可以确保伺服控制系统在参数不确定性或外部干扰下依然具有良好的性能。鲁棒控制算法会设计一个控制器，使得系统在面对各种不确定性时，依然能够保持稳定和精确的控制。

应用：适用于环境复杂、干扰多、系统参数变化较大的场景。例如，重型机械、航天器控制等复杂的伺服系统中，鲁棒控制能有效应对外界的不确定因素。

8. H∞控制

H∞控制是一种高级的鲁棒控制方法，专门设计来应对不确定性和干扰。它通过将系统的不确定性和干扰建模为一个特定频域内的增益优化问题，确保系统在各类情况下都具有较好的稳定性和性能。

应用：主要用于对系统稳定性和抗干扰能力要求极高的场景，如高精度伺服系统和航空航天中的控制系统。

PID控制器详细解释

PID控制器是工业控制中最常用的一种控制算法，全称为比例-积分-微分控制器。它通过三个部分来调节系统的输出：比例控制（P）、积分控制（I）**和**微分控制（D），每个部分都有不同的作用。PID控制器的核心思想是通过不断调节这三部分的比重来达到理想的控制效果。

PID控制器的数学表达式为：
请添加图片描述

其中：

u(t)：控制输出
e(t)：误差，即设定值与实际值之间的差异 e(t)=设定值−实际值e(t) = 设定值 - 实际值e(t)=设定值−实际值
K_p：比例增益
K_i：积分增益
K_d：微分增益

PID控制的三个部分

比例控制（P）：
- 作用：根据当前的误差值生成控制信号，比例控制输出与误差成正比。
- 优点：能够快速响应系统的误差，调整输出，适合系统较大误差时的快速调整。
- 缺点：单独使用比例控制会导致稳态误差，即当系统稳定后，仍可能存在小的误差。

请添加图片描述

比例控制反应速度快，适合粗调。

积分控制（I）：

作用：对过去的误差进行累积，使得累积的误差越来越小，从而消除稳态误差。
优点：能够消除系统的稳态误差，使得系统能够精确地达到设定目标。
缺点：积分控制会加速系统的响应，但也可能导致系统超调或震荡。

请添加图片描述

积分控制可以不断调整系统输出，以消除稳态误差。

微分控制（D）：

作用：根据误差的变化率进行控制，抑制误差变化过快，能够减小系统的震荡和超调。
优点：可以预测误差的趋势，提前对系统进行调节，增强系统的稳定性。
缺点：对噪声较敏感，在系统有较大干扰或噪声时效果不明显。

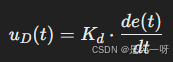
请添加图片描述

微分控制用于细调，帮助减小振荡和提高系统稳定性。

PID控制的综合作用

通过调节比例控制的响应速度、积分控制的误差消除、微分控制的提前预测，PID控制器可以实现系统的平稳、快速和精确控制。

**P（比例控制）**解决响应问题，但可能产生稳态误差。
**I（积分控制）**消除稳态误差，但可能引发超调。
**D（微分控制）**能够减少超调并提升系统稳定性。

举例：温度控制系统中的PID

假设我们有一个加热炉，用来将房间的温度保持在设定的目标温度（比如25°C）。我们用一个PID控制器来调节加热炉的功率，保持温度稳定。

目标：房间温度维持在25°C。
传感器：温度传感器测量当前房间的温度，并将数据反馈给控制器。
PID控制器的作用：
- 比例控制（P）：如果房间的实际温度低于25°C，则比例控制会根据温度差（误差）增加加热炉的功率，使房间温度上升。比如，当前温度是20°C，误差为5°C，P控制器会根据这个5°C的误差计算出一个功率输出，让加热炉工作起来。温差越大，功率越高。
- 积分控制（I）：假设房间的温度已经接近25°C，但总是差一点，比如差0.5°C。（比例控制认为误差很小了，于是减小了功率输出，但是如天气太冷，导致比例控制升温速度和环境散温速度相等）比例控制可能无法完全消除这个小的误差。此时积分控制开始起作用，它会根据这段时间累积的小误差（0.5°C）逐渐增加（对偏差进行积分（累加））加热炉的输出，直到温度完全达到25°C。
- 微分控制（D）：当温度快速上升时，微分控制能够检测到温度变化的速度，提前调节加热炉功率，让温度更平稳地接近目标，而不至于超调（温度超过25°C太多）。例如，当前温度从20°C迅速上升到24°C，D控制器会减小加热功率，避免温度冲过25°C。

import numpy as np
import matplotlib.pyplot as plt

# 时间轴
time = np.linspace(0, 20, 1000)

# 设定的目标温度
setpoint = 25

# 假设的实际温度响应（一个简单的系统响应曲线）
Kp, Ki, Kd = 2.0, 0.5, 0.2
actual_temperature = np.zeros_like(time)
error = np.zeros_like(time)
integral = 0
previous_error = 0
dt = time[1] - time[0]

# 模拟PID控制过程
for i in range(1, len(time)):
    error[i] = setpoint - actual_temperature[i-1]
    integral += error[i] * dt
    derivative = (error[i] - previous_error) / dt
    output = Kp * error[i] + Ki * integral + Kd * derivative
    actual_temperature[i] = actual_temperature[i-1] + output * dt
    
    # 设定温度不能超过系统的物理限制
    if actual_temperature[i] > 30:
        actual_temperature[i] = 30
    if actual_temperature[i] < 0:
        actual_temperature[i] = 0

    previous_error = error[i]

# 绘制图像
plt.figure(figsize=(10, 6))
plt.plot(time, actual_temperature, label="Actual Temperature (PID controlled)", color='blue', lw=2)
plt.axhline(y=setpoint, color='r', linestyle='--', label="Setpoint (25°C)")
plt.title("PID Control Example: Temperature Regulation")
plt.xlabel("Time (seconds)")
plt.ylabel("Temperature (°C)")
plt.legend()
plt.grid(True)
plt.show()