前言
时间序列预测在金融领域中具有重要意义,尤其是在股票价格的预测上。本文以 ARIMA 模型为例,探讨如何基于历史数据对股票涨跌额进行预测。由于 ARIMA 模型仅适用于单变量时间序列,本教程主要针对收盘价的变化趋势进行简单预测,并通过 AIC 和 BIC 两种模型选择标准进行性能比较。本文仅适合作为入门时间序列预测的作业示例。
教程目标
1.使用 Python 中的 statsmodels 库构建 ARIMA 模型,预测股票涨跌额。
2.通过 AIC 和 BIC 指标优化模型参数(通过遍历 (p, d, q) 参数组合,使用 AIC 和 BIC 指标选择最优模型)。
3.可视化预测结果并评估模型性能。
数据准备
在本教程中,我们假设你已经有一份本地 CSV 文件,其中包含股票的历史交易数据。
股票代码|交易日期|收盘价
例如:000001.SZ.csv
股票代码,交易日期,收盘价
000001.SZ,2019-01-02,8.50
请根据自己的数据进行相应调整。
import matplotlib.pyplot as plt
import pandas as pd
from pandas.plotting import autocorrelation_plot
from pyspark.sql import SparkSession
from pyspark.sql.functions import col, to_date
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.statespace.sarimax import SARIMAX
# 读取本地 CSV 文件
pandas_df = pd.read_csv("000001.SZ.csv", header=0)
# 转换 '交易日期' 为 datetime 类型并按日期排序
pandas_df['交易日期'] = pd.to_datetime(pandas_df['交易日期'], errors='coerce')
pandas_df.sort_values('交易日期', inplace=True)
# 去除空值行
pandas_df = pandas_df.dropna()
# 特征列
features = ['收盘价']
data = pandas_df[features]
ticker = "000001.SZ" # 股票代码
# 画出训练集合股价图像
plt.rcParams["figure.figsize"] = (10, 7)
plt.style.use('ggplot')
data.plot()
plt.title(f'{ticker}股票收盘价', fontsize=16)
plt.ylabel('价格(元)', fontsize=14)
plt.legend(['收盘价'], prop={ 'size': 12})
plt.show()
# 绘制自相关图
autocorrelation_plot(data)
plt.title(f'{ticker}股票收盘价自相关图', fontsize=16)
plt.ylabel('自相关系数', fontsize=14)
plt.show()
# 将数据按时间分割
train_set = data[data.index < '2020-01-01']
test_set = data[data.index >= '2020-01-01']
print(train_set)
print(test_set)
plt.figure(figsize=(10, 5)) # 调整图像大小
plt.title(f'{ticker}股票收盘价', fontsize=16) # 使用中文楷体
plt.xlabel('交易日期', fontsize=14)
plt.ylabel('价格(元)', fontsize=14)
plt.plot(train_set, color='green', label='训练集') # 添加图例标签
plt.plot(test_set, color='red', label='测试集') # 添加图例标签
plt.xlim(train_set.index.min(), test_set.index.max()) # 只显示有数据的部分
plt.legend(prop={'size': 12}) # 自动显示定义的标签,确保图例使用中文字体
plt.show()
# 优化ARIMA模型
aic_p = []
bic_p = []
params = [] # 用于存储(p, d, q)参数
p = range(0, 6) # [0,1,2,3,4,5]
d = range(0, 2) # [0,1]
q = range(0, 6) # [0,1,2,3,4,5]
# 三个循环遍历所有(p, d, q)
for i in p:
for j in d:
for k in q:
model = ARIMA(train_set, order=(i, j, k)) # define ARIMA model
model_fit = model.fit() # fit the model
aic_temp = model_fit.aic # get aic score
bic_temp = model_fit.bic # get bic score
aic_p.append(aic_temp) # append aic score
bic_p.append(bic_temp) # append bic score
params.append((i, j, k)) # 存储参数
print(f'ARIMA model p={i}, d={j}, q={k} AIC={aic_temp}, BIC={bic_temp}') # 输出所有模型的AIC和BIC评分
# 找到AIC和BIC最小值的索引
min_aic_index = aic_p.index(min(aic_p))
min_bic_index = bic_p.index(min(bic_p))
# 绘制AIC图像
plt.figure(figsize=(12, 6))
plt.plot(range(len(aic_p)), aic_p, color='red', marker='o')
plt.annotate(f'({params[min_aic_index][0]},{params[min_aic_index][1]},{params[min_aic_index][2]})',
(min_aic_index, aic_p[min_aic_index]), textcoords="offset points", xytext=(0, 10), ha='center')
plt.title('AIC优化模型图', fontsize=16)
plt.xlabel('模型参数', fontsize=14)
plt.ylabel('AIC评分', fontsize=14)
plt.show()
# 绘制BIC图像
plt.figure(figsize=(12, 6))
plt.plot(range(len(bic_p)), bic_p, color='blue', marker='o')
plt.annotate(f'({params[min_bic_index][0]},{params[min_bic_index][1]},{params[min_bic_index][2]})',
(min_bic_index, bic_p[min_bic_index]), textcoords="offset points", xytext=(0, 10), ha='center')
plt.title('BIC优化模型图', fontsize=16)
plt.xlabel('模型参数', fontsize=14)
plt.ylabel('BIC评分', fontsize=14)
plt.show()
# 获取 AIC 和 BIC 最优参数
best_aic_params = params[min_aic_index]
best_bic_params = params[min_bic_index]
# 使用 AIC 最优参数拟合模型
model_aic = ARIMA(train_set, order=best_aic_params)
model_fit_aic = model_aic.fit()
# 使用 BIC 最优参数拟合模型
model_bic = ARIMA(train_set, order=best_bic_params)
model_fit_bic = model_bic.fit()
print(f"最佳 AIC 参数: p={best_aic_params[0]}, d={best_aic_params[1]}, q={best_aic_params[2]}")
print(f"最佳 BIC 参数: p={best_bic_params[0]}, d={best_bic_params[1]}, q={best_bic_params[2]}")
# 使用 AIC 最优参数预测
predictions_aic = []
past_aic = train_set['收盘价'].tolist()
for i in range(len(test_set)):
model = ARIMA(past_aic, order=best_aic_params)
model_fit = model.fit(start_params=model_fit_aic.params)
pred = model_fit.forecast()[0]
predictions_aic.append(pred)
past_aic.append(test_set.iloc[i, 0])
# 使用 BIC 最优参数预测
predictions_bic = []
past_bic = train_set['收盘价'].tolist()
for i in range(len(test_set)):
model = ARIMA(past_bic, order=best_bic_params)
model_fit = model.fit(start_params=model_fit_bic.params)
pred = model_fit.forecast()[0]
predictions_bic.append(pred)
past_bic.append(test_set.iloc[i, 0])
# 分别评估 AIC 和 BIC 模型的性能
from sklearn.metrics import mean_absolute_error, mean_absolute_percentage_error
# AIC:
mse_aic = mean_squared_error(test_set, predictions_aic)
mae_aic = mean_absolute_error(test_set, predictions_aic)
mape_aic = mean_absolute_percentage_error(test_set, predictions_aic)
print('Test MSE: {mse}'.format(mse=mse_aic))
print('Test MAE: {mae}'.format(mae=mae_aic))
print('Test MAPE: {mape:.2%}'.format(mape=mape_aic))
# BIC:
mse_bic = mean_squared_error(test_set, predictions_bic)
mae_bic = mean_absolute_error(test_set, predictions_bic)
mape_bic = mean_absolute_percentage_error(test_set, predictions_bic)
print('Test MSE: {mse}'.format(mse=mse_bic))
print('Test MAE: {mae}'.format(mae=mae_bic))
print('Test MAPE: {mape:.2%}'.format(mape=mape_bic))
plt.figure(figsize=(12, 6))
plt.plot(test_set.index, test_set, color='green', label='实际值')
plt.plot(test_set.index, predictions_aic, color='red', label='AIC 最优预测值')
plt.plot(test_set.index, predictions_bic, color='blue', label='BIC 最优预测值')
plt.title(f'{ticker}股票预测对比', fontsize=16)
plt.xlabel('日期', fontsize=14)
plt.ylabel('价格(元)', fontsize=14)
plt.legend(prop={'size': 12})
plt.show()
结果展示
1.通过绘制收盘价和自相关图观察数据趋势:



2.通过 AIC 和 BIC 曲线直观比较不同参数组合的性能:



3.预测结果对比图:

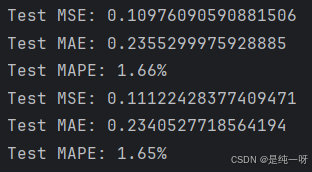
4.使用 MSE、MAE 和 MAPE 指标评估模型效果:
总结
通过本文,上述就是如何使用 ARIMA 模型进行时间序列预测,并通过 AIC 和 BIC 指标选择最优参数。最终的预测结果展示了 ARIMA 模型的基本能力,但需要注意的是:
ARIMA 模型适用于较规则的时间序列,可能无法很好地处理股票的复杂波动。
本文仅作为作业示例,实际应用中需结合更复杂的模型(如深度学习)以提高预测效果。
























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








