Simulink仿真---SVPWM算法

一、理论

SVPWM算法的具体讲解在这里：https://blog.csdn.net/qlexcel/article/details/74787619

1、判断扇区

根据下面3个式子：

    再定义，若U1 > 0 ，则 A=1，否则 A=0； 

                  若U2 > 0 ，则B=1，否则 B=0；

                  若U3 > 0 ，则 C=1，否则 C=0。

    可以看出 A，B，C 之间共有八种组合，但由判断扇区的公式可知 A，B，C 不会同时为 1 或同时为 0，所以实际的组合是六种，A，B，C 组合取不同的值对应着不同的扇区，并且是一一对应的，因此完全可以由 A，B，C 的组合判断所在的扇区。为区别六种状态，令 N=4*C+2*B+A，则可以通过下表计算参考电压矢量Uref所在的扇区。

2、计算各矢量作用时间

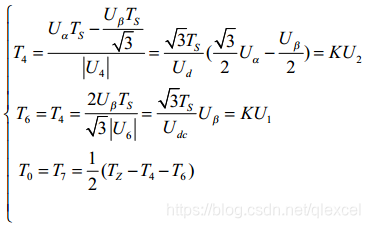
        同理可求得Uref在其它扇区中各矢量的作用时间，结果如表2-4所示。表中两个非零矢量作用时间的比例系数为K =√3Ts/Udc 。

各扇区作用时间：

3、确定扇区矢量切换点（如扇区1中，矢量0到矢量4的切换点，矢量4到矢量6的切换点）

二、建模

1、添加扇区判断的子系统（根据输入的Ualpha和Ubeta判断电压矢量所在扇区）：

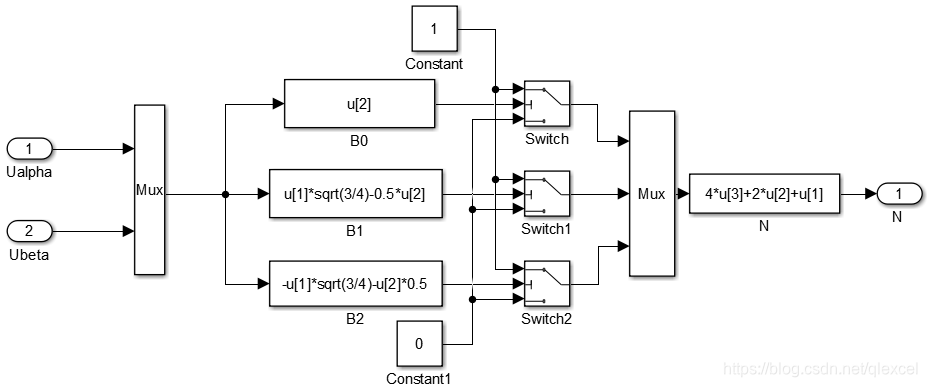
switch模块设置为：（条件为u2>=0，如果满足u1通过，如果不满足，u3通过）

2、计算X、Y、Z，用于计算扇区矢量作用时间（输入Ualpha、Ubeta、母线电压Udc、载波周期时间Ts，计算X、Y、Z）。

3、根据N值和X、Y、Z来计算扇区中矢量的作用时间（输入XYZ、N值、载波周期Ts，计算扇区中矢量作用时间）

Mutiport Switch模块根据最上面输入的N值选择下面的那个端口通过。配置如下：

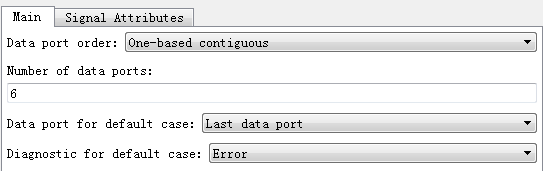
如：N=1，则Mutiport Switch模块输出为T1=Z、T2=Y，再根据Ts-Z-Y是否大于零来判断是否过调制。如果过调制，还要用上面给的比例公式，把Z和Y矫正一下再输出。

4、扇区矢量切换点的确定

实现上是计算3个PWM通道输出电平的改变点。我们知道SVPWM中定时器是配置为中央对齐模式：

要在每个载波周期中改变输出通道的比较值，而计算出的Tcm1、Tcm2、Tcm3分别就是3个通道的比较值。

5、计算出了每个载波周期3个通道的比较值，再引入定时器的中央对齐模式，就可以输出逆变桥的控制信号了。（此处用三角波模拟定时器中央对齐模式）

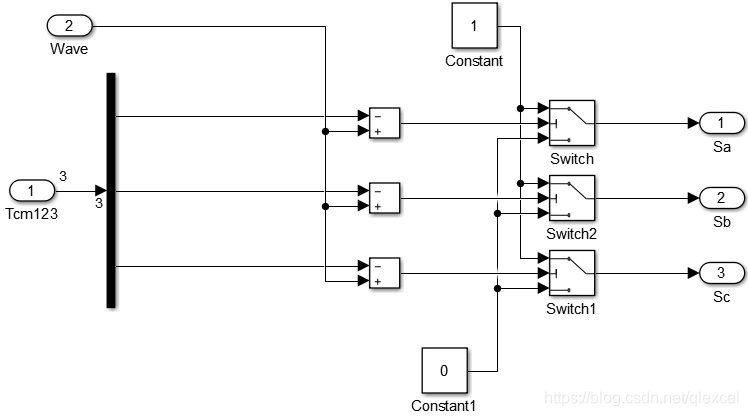
输入一个三角波模拟定时器中央对齐模式，用三角波当前值和通道比较值做对比，如果三角波的值大于通道比较值就输出高电平，如果小于就输出低电平。

6、使用3个通道的PWM控制逆变桥，计算相电压

以其中一种开关组合为例分析，假设Sx(x=a、b、c)=(100)，此时等效电路如图：

因此相电压可以表示为：（相电压是每相相对于电机中间连接点的电压）

从电阻分压的原理，可以知道相电压共有4种输出：1/3Udc、-1/3Udc、2/3Udc、-2/3Udc。因此上面的模型中，根据3个通道的电平状态来判断相电压输出这4中电压中的哪一个。如Sa、Sb、Sc都输入1，则经过逻辑运算后，到了Product模块，从上到下依次为：0，0，0，0，因此输出0.

7、最后总模型为：

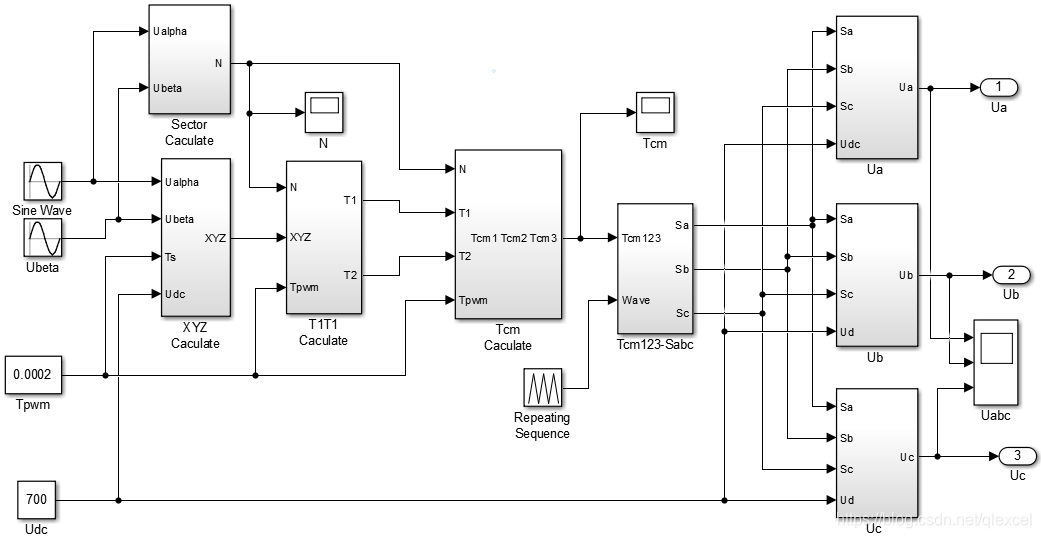
1）、正弦波信号源配置：

输入角速度为100π，幅值为200，相位互差90度的正弦波。角速度为100π，则周期为0.02，频率为50Hz，这个是电压矢量的旋转速度，即3000RPM。如果是一对极电机，转速就为3000RPM。

2）、Tpwm模块输入载波周期，此处载波为5KHz，所以值为0.0002秒。

3）、三角波信号源配置：（即载波为5KHz）

8、仿真结果

N值变化的波形：

定时器通道比较值的波形，3个通道，波形呈马鞍形

定时器通道比较值的波形、三角载波、PWM控制波形：

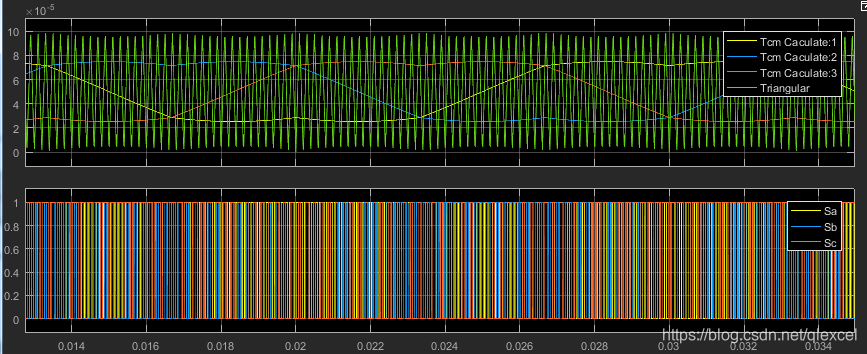
放大：

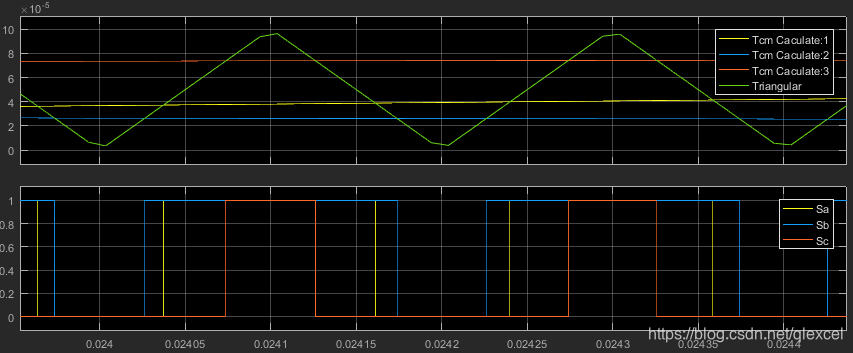
扇区N和3个通道PWM控制波形：

相电压波形：

放大：

最后从下面位置加入powergui模块做FFT分析

仿真完后，双击powergui模块，打开FFT Analysis：

配置如下，分析Ua的基波幅值：

可以看到50Hz的基波幅值为199.9V，与实际值200V相符。此仿真结果验证了模型的正确性。

 

模型文件下载：https://download.csdn.net/download/qlexcel/11516270

注：模型来自《现代永磁同步电机控制原理及MATLAB仿真》__袁雷编著