机器学习之降维

机器学习之降维

$$过拟合=\{\begin{array}{rl}& data\uparrow \\ & 正则化\\ & 降维\{\begin{array}{rl}& 直接降维:特征选择\\ & 线性降维:PCA,MDS\\ & 非线性降维:\{\begin{array}{rl}& 保留局部特征\{\begin{array}{rl}& 局部重建权值:LLE\\ & 邻接图:LaplacianEigenmaps\end{array}\\ & 保留全局特征\{\begin{array}{rl}& 流形:Isomap、LPP\\ & 基于核函数:KPCA、KICA\end{array}\end{array}\end{array}\end{array}$$

维度灾难

在机器学习中，过拟合问题是我们常见的一个问题，而解决它的方法除了正则化和增加数据之外，降维也是一个非常不错的方法。数据降维可以将较高维度数据转换为较低维度数据进行表达，同时最大程度上保留原有数据间的关系。
降维的思路来源于维度灾难的问题，我们知道 $n$ 维球的体积为：
$$C{R}^n$$
那么在球体积与边长为 $2R$ 的超立方体比值为：
$$\underset{n\to 0}{\lim }\frac{C{R}^n}{2^n{R}^n}=0$$

这就是所谓的维度灾难，在高维数据中，主要样本都分布在立方体的边缘，所以数据集更加稀疏。

---

本文将从以下几个方面讲解代码实操

• 主成分分析（PCA）：使转换后各维度上样本方差最大化的线性降维方法。
• 线性判别分析（LDA）：与PCA类似，在生成新维度时多考虑了每种标签样本数据集内的分布情况。
• 多维标度法（MDS）: 保留距离信息的线性变换。
• 流形基础：什么是流形、局部欧几里得空间、测地线距离等。
• 等距映射（Isomap）：在降维后保持近邻点间结构不变的流形学习方法。
• 局部线性嵌入（LLE）：假设样本在局部区域内满足线性关系的流行学习方法。
• 谱聚类：先用Laplacian Eigenmaps进行流形降维、再聚类的方法。
• t-SNE：用概率建模的流形学习方法。

PCA

主成分分析中，我们的基本想法是将所有数据投影到一个子空间中，从而达到降维的目标，为了寻找这个子空间，我们基本想法是：

1. 所有数据在子空间中更为分散
2. 损失的信息最小，即：在补空间的分量少

原来的数据很有可能各个维度之间是相关的，于是我们希望找到一组 $p$ 个新的线性无关的单位基 $u_i$，降维就是取其中的 $q$ 个基。于是对于一个样本 $x_i$，经过这个坐标变换后：
$$\widehat{x_i}=\sum _{i=1}^p(u_i^T{x}_i)u_i=\sum _{i=1}^q(u_i^T{x}_i)u_i+\sum _{i=q+1}^p(u_i^T{x}_i)u_i$$
对于数据集来说，我们首先将其中心化，然后再取上面的式子的第一项，并使用其系数的平方平均作为损失函数并最大化：
$$\begin{array}{rl}J& =\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^q((x_i-\overline{x}{)}^T{u}_j{)}^2\\ & =\sum _{j=1}^q{u}_j^{T}S{u}_j,\\ s.t.u_j^T{u}_j=1& \end{array}$$
由于每个基都是线性无关的，于是每一个 $u_j$ 的求解可以分别进行，使用拉格朗日乘子法：
$${\mathrm{argmax}}_{u_j}J(u_j,\lambda )={\mathrm{argmax}}_{u_j}{u}_j^{T}S{u}_j+\lambda (1-u_j^T{u}_j)$$
于是：
$$S{u}_j=\lambda u_j$$
可见，我们需要的基就是协方差矩阵的特征向量。损失函数最大取在特征值前的 $q$ 个最大值。

下面看其损失的信息最少这个条件，同样使用系数的平方均值作为损失函数，并最小化：
$$\begin{array}{rl}J& =\frac{1}{N}\sum _{i=1}^N\sum _{j=q+1}^p((x_i-\overline{x}{)}^T{u}_j{)}^2\\ & =\sum _{j=q+1}^p{u}_j^{T}S{u}_j,s.t.u_j^T{u}_j=1\end{array}$$
同样的：
$${\mathrm{argmin}}_{u_j}J(u_j,\lambda )={\mathrm{argmin}}_{u_j}{u}_j^{T}S{u}_j+\lambda (1-u_j^T{u}_j)$$
损失函数最小取在特征值中剩下的最小的几个值。

LDA

由于无监督学习中样本数据没有分类标签，所以 PCA 在为样本集定义全新的特征维度时要考虑所有的样本数据。而LDA可以看成在有数据标签时的PCA样本，它将寻找新的特征映射正交基时的目标从"最大化所有样本在新维度上的方差"改为"最大化类间样本的方差、最小化类内样本的方差"(类间大,类内小)。

sklearn

在scikit-learn中实现了PCA和LDA模型,其调用方法通过三步完成：

1. 初始化PCA或LDA对象，同时传入降维目标参数n_components。
2. 调用fit（）函数用原始数据训练模型。
3. 调用transform（）函数获得降维后的数据。

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

iris = datasets.load_iris()
X = iris.data
y = iris.target

plt.subplot(131)
for name, label, m in [('Setosa', 0, "<"), ('Versicolour', 1, "o"), ('Virginica', 2, ">")]:
    plt.scatter(X[y==label, 0], X[y==label,1], label=name, marker=m)
plt.legend()
plt.title("data shape:%s"%(X.shape,))

# PCA降维
plt.subplot(132)
pca = PCA(n_components=2)
pca.fit(X)
X_pca = pca.transform(X)

for name, label, m in [('Setosa', 0, "<"), ('Versicolour', 1, "o"), ('Virginica', 2, ">")]:
    plt.scatter(X_pca[y==label, 0], X_pca[y==label,1], label=name, marker=m)

plt.legend()
plt.title("PCA")
# 降维后各维度上的方差比,方差比越高,说明该维度的信息保留度越高。
print('PCA:',pca.explained_variance_ratio_)

# LDA
plt.subplot(133)
lda = LDA( n_components=2).fit(X, y)
X_lda = lda.transform(X)

for name, label, m in [('Setosa', 0, "<"), ('Versicolour', 1, "o"), ('Virginica', 2, ">")]:
    plt.scatter(X_lda[y==label, 0], X_lda[y==label,1], label=name, marker=m)
plt.legend()
plt.title("LDA")
print('LDA:',lda.explained_variance_ratio_)

plt.show()

PCA: [0.92461872 0.05306648]
LDA: [0.9912126 0.0087874]

PCA降维后两个维度的"方差比和"小于1，说明降维没有完全保留原始信息，有一小部分信息被丢失了；LDA降维后的"方差比和"等于1，说明其完全保留了原始信息。

MDS

多维标度法（Multi-Dimensional Scaling,MDS）最初是心理学的一个度量工具，用以理解人们判断的相似性，被广泛应用于市场调研、心理学数据分析。MDS 主要用于解决"已知样本两两之间的距离，如何恢复所有样本坐标"的问题。由于样本之间的距离可来源于任意高维空间，而恢复出的坐标却可以表现在相对低维的空间里，因此 MDS 成为了一种重要的降维模型。

从降维的角度考虑，MDS与PCA有相同的使用场景，它们都是无监督的线性降维方法。但是它们在线性变换中的优化
目标不同，PCA目标是在新维度上产生最大的样本方差，而MDS的目标是“降维前后样本之间的距离尽量保持一致”。

MDS的降维计算过程

1. 生成样本距离矩阵D。
   计算两两样本之间的距离将其转换成N阶样本距离方阵D，其中N是样本数量，D中的元素$d{i}_j$是第i个样本与第j个样本之间的距离，值越高说明两个样本差异越大。$d{i}_j$可以采用欧式距离、马氏距离、杰卡德相似度、DTW等任意距离计量方式。

2. 理解相似度矩阵B
   相似度矩阵也是一个N阶方阵，其元素$b{i}_j$值越高说明样本i和j越相似。在向量空间中，内积恰巧就是表示单元向量相似度的方式。也就是说，矩阵B就是样本向量的内积矩阵，这样将B分解为$X{X}^T$后，就能得到样本向量 X 了。所以后续对 B 进行特征值分解后再分解为$X{X}^T$形式可以达到降维的目的。

3. 特征值分解提取主要成分
   后面的步骤与PCA和LDA中的特征值分解类似，通过保留大的特征值对应的特征向量，来提取被分解矩阵的主要成分，得到主成分相似度矩阵B*，直接对其分解为$X{X}^T$后获得降维后的样本集X。

MDS的重要变形

1. NMDS
   传统 metric MDS精确地计量样本之间的距离并在降维中保留该距离。但是在有些场景中只关心样本间距离的大小顺序，而不是精确的距离值，这样的 MDS 被称为 non-metric MDS，简称为NMDS；传统metric MDS有时也被简称为CMDS（classic MDS）。

举例，假设原始特征空间中的三个样本 a、b、c 之间有距离关系distance（a,b）=distance（a,c）+p，其中p是任意正值，则在降维后只需保证距离不等式distance（a,b）＞distance（a,c），而无须确切地保留p值。对于这样的降维需求，在 NMDS 中定义了损失函数 STRESS 作为优化目标控制距离矩阵D的计算。STRESS基于样本之间的距离迭代计算而来，NMDS的目标是使STRESS最小化。一个比较普及的最小化 STRESS 的算法称为 SMACOF（StressMajorization of a Complicated Function）。由于metric MDS可以看成NMDS的极端情况，STRESS和SMACOF后来也被用来计算metricMDS。

2. CMDS与PCA的关系
   MDS与PCA都是无监督的降维模型，且在计算过程中都用到了特征值分解后提取主要特征向量。在MDS中被特征值分解的矩阵是样本内积矩阵B，而在PCA中被特征值分解的是均值化后样本的协方差矩阵C。如果在MDS计算距离矩阵D的时候使用欧式距离，则内积矩阵B可以通过线性变换转换成协方差矩阵C。因此，可以将PCA看成CMDS在使用欧式公式计算原始样本距离时的一种特殊情况，PCA与使用欧式距离的CMDS在降维效果上没有区别。

sklearn实战

在sklearn.manifold 中实现了 MDS 模型，通过调用fit_transform（）函数可完成降维转换，该模型比较重要的初始化参数如下：

• n_components：降维后的维度数。
• metric:True或False，表示使用metric MDS算法或non-metric MDS算法。
• n_init、max_iter、eps：在SMACOF算法中控制STRESS计算的参数。
• dissimilarity:euclidean或precomputed，如果是euclidean则在执行fit（）函数时传入原始特征向量；如果是 precomputed 则在执行 fit（）函数时传入计算好的距离矩阵D，可以用任何距离公式计算该矩阵。

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.manifold import MDS

# 加载数据
iris = datasets.load_iris()
X = iris.data
y = iris.target

# PCA
plt.subplot(121)
pca = PCA(n_components=2)
pca.fit(X)
X_pca = pca.transform(X)

for name, label, m in [('Setosa', 0, "<"), ('Versicolour', 1, "o"), ('Virginica', 2, ">")]:
    plt.scatter(X_pca[y==label, 0], X_pca[y==label,1], label=name, marker=m)
plt.legend()
plt.title("PCA")
print('PCA:',pca.explained_variance_ratio_)


#MDS
plt.subplot(122)
mds = MDS(n_components=2, metric=True)
X_mds = mds.fit_transform(X)

for name, label, m in [('Setosa', 0, "<"), ('Versicolour', 1, "o"), ('Virginica', 2, ">")]:
    plt.scatter(X_mds[y==label, 0], X_mds[y==label,1], label=name, marker=m)
plt.legend()
plt.title("MDS")

plt.show()

PCA: [0.92461872 0.05306648]

左图是 PCA，右图是 MDS。将左图左右翻转后稍作逆时针旋转的效果，其结果就与右图非常相近了

上面分析了在使用欧氏距离时，metric MDS 与 PCA 本质的一致性，之所以 MDS 降维后的数据方向无法与 PCA 保持一致。 是因为 MDS 将原始坐标转换成距离矩阵后进行降维，而这一转换丢失了原始数据中各样本的方位特性。

Isomap

Isomap是非线性降维的主要方法，是最好的流形入门模型，是MDS在流形语境下的直接扩展。

流形的定义

Wiki：流形（manifold）是局部具有欧几里得性质的空间，通常嵌入比该局部空间更高维的外围非欧几里得空间中。Manifold（流形）=many+fold（小平面）也就是说流形是若干个欧几里得空间的拼接，这里的"Many"可以是有限的个数，也可以是无限多个。

流形学习的概念于2000年在 Science杂志上被提出，其代表算法是Isomap和 LLE。流形学习的目的就是将嵌入在外围空间（AmbientSpace）中的流形提取到与其内蕴空间（Intrinsic Space）同构的新的低维空间中。

用地球作为一个流形举例：以宇宙视角俯视的三维空间是地球所在的外围空间，如果忽略地球不同地区的海拔差异，则地球表面的局部区域就是二维的内蕴空间，而二维地图则可看成对地球进行流形学习后的降维结果。当然，对于地球仪这样理想的简单流形，仅通过简单的坐标映射就可以完成从三维空间到二维空间的转换，根本不需要使用流形学习。流形学习真正要解决的是各种嵌入在高维空间中的不规则流形。

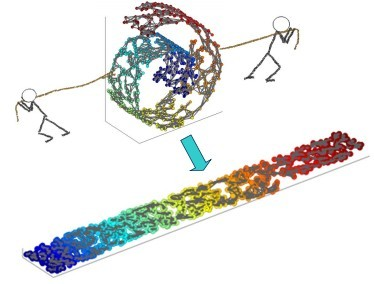
图中的流形是一条卷曲在三维空间中的二维彩带，流形学习的理想结果是将其展开平铺在二维空间中。这样的流形学习一般可以通过两步来完成：

• 识别出外围空间中组成局部欧几里得空间的样本，并计算样本之间的距离。
• 将这些距离等距重构（isometry）到低维空间完成降维，MDS就是典型的等距重构算法。

流形的适用性分析

1. 就像 PCA 等要求高维空间本身有信息冗余，流形学习也仅适用于流形嵌入比较明显的场景。
2. 流形的基础是局部的欧几里得空间，所以在流形学习中要求有足够密集的数据样本能让算法检测到局部空间。就像上图中的样本数据几乎是一整条彩带而没有隔断。
3. 流形学习一般对噪声比较敏感，如果在上图中的彩带卷中间有噪声数据，则可能会被识别为堆状流形，而非带状流形。

测地线距离

Isomap的基本原理是用测地线计算样本之间的欧几里得距离，然后用该距离进行 MDS 降维。

测地线的计算：在流形结构未知，数据采样有限的情况下， 通过构造数据点间的邻接图(Graph)，用图上的最短距离来近似测地线距离，当数据点趋于无穷多时，这个估计近似距离趋向于真实的测地线距离。

Isomap流形降维的三步流程:

1. 找出所有样本点的邻近样本点，它定义了流形理论中的"局部欧几里得空间"。邻近点可以用"最近的k个邻居"或"距离d以内的所有邻居"等策略选取。
2. 利用上一步建立的临近点图，计算所有样本点之间的最短路径，生成测地线距离矩阵。最短路径可以用Dijkstra、Floyd等图论经典算法计算。
3. 将测地线距离矩阵输入MDS/kernelPCA模型，完成降维。

KernelPCA是用核函数计算样本协方差矩阵的PCA算法，使PCA也有了非线性学习能力。之前讨论过 CMDS 与 PCA 的本质一致性；相应地，非线性的 MDS 与 kernelPCA也有本质一致性。因此在实践中，MDS和kernelPCA都可以作为Isomap的降维算法。

Isomap实战

在sklearn.manifold 中实现了 Isomap 模型，通过fit（）、transform（）等函数可以直接完成Isomap的训练和降维。
模型初始化参数如下:

• n_neighbors：寻找样本近邻时"最近的k个邻居"中k的值。
• n_components：降维后的维度数量。
• eigen_solver：计算矩阵特征值的算法，arpack使用 Arnoldi迭代算法，适用于稀疏矩阵，dense使用直接解法，适用于稠密矩阵。
• tol、max_iter：控制Arnoldi算法的迭代参数。
• path_method：测地线最短路径的生成算法，FW 使用 Floyd-Warshall，时间复杂度是$O(N^3)$。D 使用 Dijkstra 算法，时间复杂度是$O(N^2(K+log(N)))$，其中 N 是样本数量，k是原始维度数。
• neighbors_algorithm：近邻搜索算法，可选brute、kd_tree、ball_tree。

在模型训练后，可以通过如下属性获得学习结果：

• embedding_：样本降维后的结果。
• kernel_pca_:使用 KernelPCA 作为降维算法，可以通过本属性读取KernelPCA对象。
• nbrs_：以sklearn.neighbors.NearestNeighbors对象表达的样本近邻结构。
• dist_matrix_：测地线距离矩阵。

import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.manifold import Isomap

# 加载数据
iris = datasets.load_iris()
X = iris.data
y = iris.target

plt.figure(figsize=(10,10))
# PCA
plt.subplot(221)
X_pca = PCA( n_components=2).fit_transform(X)

for name, label, m in [('Setosa', 0, "<"), ('Versicolour', 1, "o"), ('Virginica', 2, ">")]:
    plt.scatter(X_pca[y==label, 0], X_pca[y==label,1], label=name, marker=m)
plt.legend()
plt.title("PCA")

# Isomap
for idx, neighbor in enumerate([2, 20, 100]):
    plt.subplot(222 + idx)
    isomap = Isomap(n_components=2, n_neighbors=neighbor)
    X_isomap = isomap.fit_transform(X)

    for name, label, m in [('Setosa', 0, "<"), ('Versicolour', 1, "o"), ('Virginica', 2, ">")]:
        plt.scatter(X_isomap[y==label, 0], X_isomap[y==label,1], label=name, marker=m)
    plt.legend()
    plt.title("Isomap (n_neighbors=%d)"%neighbor)

plt.show()

n_neighbors 值越小，流形上的局部欧几里得空间越小，降维后样本间的排列效果越明显；n_neighbors值越大，测地线距离越接近外围空间的欧几里得距离，使得Isomap更接近普通PCA的结果。

当近邻数是2时，样本间只能"一个接一个"的看到其他样本，因此降维后呈右上图效果；而当近邻数达到100时，Isomap与PCA的效果已经完全一样。

流行学习之局部嵌入

Isomap在降维中需要计算所有样本之间的测地线距离,而局部线性嵌入(LLE)和拉普拉斯特征映射(LE)等多种局部嵌入类算法只考虑相互领近样本间的关系。

LLE

LLE是一种以保持每个样本与邻近样本之间距离作为降维目标的流形学习方法,它假设某个点$x_i$坐标可以由它周围的一些点的坐标线性组合求出。通过一个邻近权重系数矩阵 W 记录每个样本与邻近样本之间的关系，并试图在降维后保持该权重矩阵。

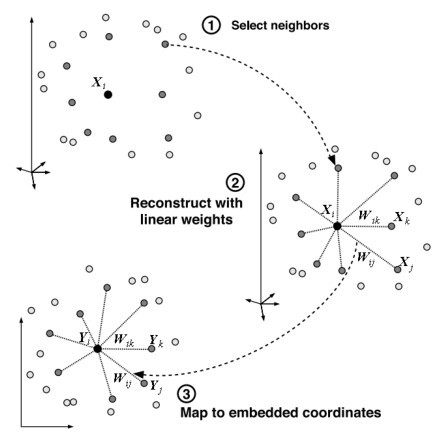
LLE算法的提出者Lawrence K.Saul 形象地用上图描述了LLE原理。

LLE降维过程

1. 寻找每个样本点的k个近邻点；
2. 由每个样本点的近邻点计算出该样本点的局部重建权值矩阵；
3. 由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。

LE

拉普拉斯特征映射（Laplacian Eigenmaps,LE）是与LLE非常像的一个局部嵌入降维方法。它们的不同之处在于LLE围绕尽量保持权重系数的矩阵进行降维，而LE围绕保持拉普拉斯的矩阵（Laplacian Matrix）进行降维。

拉普拉斯矩阵是图论中一种用于表示无向有权图结构的矩阵，它由两部分组成，即拉普拉斯矩阵L=D−W，其中D是度矩阵，W是邻接权重矩阵。W中的每个元素是两个点之间边的权值；而D是对角矩阵，其对角线元素是该点所有边的权值和。

在LE中，W矩阵中的值用来表示样本之间的相似度，即距离越近的样本点权值越高，具体可以有如下三种策略:

• 只保留距离最近的k个近邻的相似度，其他较远样本权值设为0。
• 只保留距离为ε以内的近邻的相似度，其他较远样本权值设为0。
• 保留每个结点与所有其他结点的相似度。

其中前两种策略都是"局部"策略，而第三种退化为一种类似Isomap的全局策略。局部策略会导致 W 中存在大量的0而成为稀疏矩阵，在后续计算中有很大的性能优势。

谱聚类

谱聚类（Spectral clustering）是一种聚类模型，它相对K-means具有计算代价低、适应非凸数据集等特点，特别适应于高维数据的聚类。它与拉普拉斯特征映射有密切联系：谱聚类=拉普拉斯映射+K-means聚类

假设目标聚类分组数是k，谱聚类就是在对样本执行LE降维到k维后执行centers=k的K-means聚类。该过程决定了谱聚类的如下特性：

• 由于 LE 可以减少大量的样本数据维度数，使得在计算性能上比直接在高维数据上聚类的K-means等算法有大的飞跃。
• 由于流形学习是非线性算法，所以谱聚类能适应复杂的非凸数据集。
• 流形学习本身对噪声非常敏感，所以谱聚类对噪声的适应有所欠缺。

sklearn实战

在 sklearn.manifold 中提供了 LLE 和 LE 模型的实现类LocallyLinearEmbedding 和SpectralEmbedding。其中LocallyLinearEmbedding不仅实现了标准LLE模型，还可以通过它使用从LLE衍生的Modified Locally LinearEmbedding（MLLE）、Hessian Based LLE（HLLE）、Local tangentspace alignment（LTSA）等模型。
这三种衍生模型只在LLE三步求解中的第二步与标准LLE有所不同。MLLE和HLLE均是为了解决LLE近邻数大于目标维度数时产生的权重矩阵不能满秩的问题；而LTSA用局部几何分布替代权重矩阵表达近邻关系。

LocallyLinearEmbedding

LLE模型的关键初始化参数如下:

• n_neighbors：每个样本的近邻数量。
• n_components：降维后的目标维度数。
• reg：权重矩阵的正则化常数，标准LLE用它来防止权重矩阵不满秩。
• eigen_solver：特征值分解算法，与Isomap一样可以选择arpack或dense。
• method：可以是standard、hessian、modified 或ltsa，对应标准LLE和它的三种衍生模型。
• neighbors_algorithm：近邻搜索算法，可选brute、kd_tree、ball_tree。

在模型训练过后，可以读取如下属性获得降维结果:

• embedding_vectors_：低维空间中的样本向量，即降维结果。
• reconstruction_error_：降维后的权重矩阵重建误差。
• nbrs_：每个样本的近邻数。

SpectralEmbedding

LE模型的关键初始化参数如下:

• n_neighbors：每个样本的近邻数量。
• n_components：降维后的目标维度数。
• affinity：邻接矩阵 W 中样本相似度的计算方法，nearest_neighbors表示只计算n_neighbors个近邻的相似度，rbf用核函数计算全连接相似度，precomputed需调用者自行计算。

在模型训练过后，可以读取如下属性获得降维结果:

• embedding_：降维结果。
• affinity_matrix_：邻接权重矩阵。

SpectralClustering

在 sklearn.cluster 中的 SpectralClustering 类实现了谱聚类模型。
对象的初始化参数也基本是LE和K-means模型参数的组合:

• n_clusters:K-means聚类目标分组数。
• eigen_solver:LE特征值分解算法，与Isomap一样可以选择arpack或dense。
• n_init:K-means聚类次数。
• affinity:LE模型中邻接权重矩阵值的计算方式。
• n_neighbors:LE模型中每个样本近邻数量。
• assign_labels：由于 K-means 依赖于随机初始化的中心点，本参数允许在聚类步骤中使用除K-means外的discretize算法，它比K-means的结果更稳定。

在模型训练后，有两个属性可以读取:

• finity_matrix_:LE模型生成的邻接权重矩阵。
• bels_：给每个训练样本赋予的标签，即聚类结果。

因为谱聚类需要将所有数据放在一起执行LE降维，谱聚类模型没有predict（）函数，即无法在训练后利用已有模型聚类新数据。使用者只能通过 fit_predict（）返回值获得训练数据的聚类结果，或者直接读取模型labels_参数。

流行学习之t-SNE

T分布随机近邻嵌入（t-distributed Stochastic NeighborEmbedding,t-SNE）是一种使用概率方法建模的流形学习降维方法。它诞生于2008年，最初用于高维数据的可视化。从降维效果来看t-SNE像是一个流形学习终极武器，而缺点是在训练时间方面较其他模型有明显增加。

在学习了Isomap、LLE、LE 等方法后，对流形学习的核心步骤有了明确的认识：

• 用某种方式表达高维和低维空间样本之间的亲缘性（对 Isomap 来说是相似度，对LLE来说是近邻权重矩阵、对LE来说是拉普拉斯矩阵）。

• 以亲缘性尽量不变为优化目标，用拉格朗日算子或特征值分解求得低维映射。而在t-SNE中仍然是这样从定义亲缘性到求解优化目标的过程，略有不同的是：高维空间与低维空间的亲缘性并非用相同的方式表达，前者使用高斯分布，后者使用t-分布。

• 以两个分布的Kullback-Leiber散度最小作为优化目标。

由于高维空间与低维空间使用不同的概率函数，因此两者的亲缘矩阵无法直接比较。而Kullback-Leiber散度是一种衡量两个概率分布相似程度的手段，KL散度值越低表示两个概率分布越接近。因此t-SNE以最小化KL散度作为降维优化的目标:

$$\begin{array}{r}J(Y)=KL(P||Q)=\sum _{i,j}{p}_{ij}log\frac{p_{ij}}{q_{ij}}\end{array}$$

使用t-分布的原因

在 t-SNE 出现之前有一个 SNE 模型，它是一个在高维和低维空间都使用高斯分布的模型。SNE具有两个问题：

• 不对称问题：损失函数中的 KL 散度具有不对称性，导致 SNE 更加关注局部结构，相比忽略了全局结构。
• 拥挤问题：从高维空间映射到低维空间后，不同类别的簇容易挤在一起，无法较好地区分开。

流形学习的拥挤问题:

在之前的流形学习模型中，几乎都围绕着"将近邻样本在高维空间中的相互距离尽量保持不变地映射到低维空间"这个主题而进行。这几乎是流形学习理论的出发点，但这个目标是否真的可行呢?

试想这样一个问题：在一个d维空间中，最多可以有多少个不同的点相互之间有相同距离？如果是0维空间，显然所有的点之间距离都相同，因此该值为1；而1维空间是一条直线，则任取两个点后在该直线上再也找不到第三个点与它们的距离都相同；在2维空间中，任取一个等腰三角形后，再也没有第四个点能到三个顶点距离与三角形的边等长。
以此类推：在d维空间中，最多可以有d+1个点相互之间的距离相同。也就是说，在高维空间等距的n个点，映射到维度数小于n−1的低维空间后根本不可能保持等距！这就是流形学习必须面对的拥挤问题。

在t-SNE中用t-分布代替高斯分布拟合低维样本则在一定程度上解决了拥挤问题。

sklearn实战

在sklearn.manifold.TSNE中对t-SNE模型进行封装，重要参数如下。

• n_components：降维后的维度数。
• perplexity：用于调节流形中近邻的数量，通常取值范围在5～50之间，值越大在计算每个样本高斯分布的方差时使用的近邻越多。
• learning_rate、n_iter、min_grad_norm：使用梯度下降优化KL散度值时的学习速度、最大迭代次数、迭代停止阈值。
• metric：计算近邻距离的方法，缺省euclidean代表欧几里得空间距离。
• init：梯度下降开始点的选取方式，可以是random、pca或自定义低维样本值。
• method、angle：关于t-SNE重要衍生Barnes-Hut t-SNE算法的参数，该算法可以使梯度下降的时间复杂度从$O(N^2)$降低到$O(N\cdot logN)$。

在完成模型训练后，可以读取如下模型属性:

• embedding_：降维后的低维空间样本值。
• kl_divergence_：梯度下降找到的最优Kullback-Leibler值。
• n_iter_：训练样本进行的梯度下降迭代次数。

模型对比

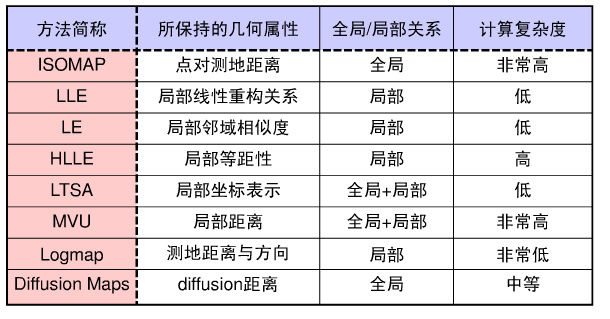
将三维空间中的一个 S 状流形降到两维为目标，分别使用了PCA、LDA、MDS、Isomap、LLE及其两种衍生模型LE和t-SNE

from time import time

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import NullFormatter

from sklearn import manifold, datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

n_points = 1000
# 生成S状流形的1000个样本点，将三维特征数据保存在变量X中，将标签数据保存在color变量中
X, color = datasets.make_s_curve(n_points, random_state=0)
n_neighbors = 10
n_components = 2

fig = plt.figure(figsize=(15, 8))
plt.suptitle("Dimension Reduction with %i points, %i neighbors"
             % (1000, n_neighbors), fontsize=14)


ax = fig.add_subplot(251, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
# 改变视角
ax.view_init(4, -72)

methods = ['standard', 'ltsa', 'hessian', 'modified']
labels = ['LLE', 'LTSA', 'Hessian LLE', 'Modified LLE']

for i, method in enumerate(methods):
    if i>2:
        continue
    t0 = time()
    Y = manifold.LocallyLinearEmbedding(n_neighbors, n_components,
                                        eigen_solver='auto',
                                        method=method).fit_transform(X)
    t1 = time()
    print("%s: %.2g sec" % (methods[i], t1 - t0))

    ax = fig.add_subplot(252 + i)
    plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
    plt.title("%s (%.2g sec)" % (labels[i], t1 - t0))
    ax.xaxis.set_major_formatter(NullFormatter())
    ax.yaxis.set_major_formatter(NullFormatter())
    plt.axis('tight')

    
estimators = [(manifold.Isomap(n_neighbors, n_components), "Isomap"), 
              (manifold.MDS(n_components, max_iter=100, n_init=1), "MDS"),
              (manifold.SpectralEmbedding(n_components=n_components,
                                          n_neighbors=n_neighbors), "Laplace Eigenmaps"),
              (manifold.TSNE(n_components=n_components, init='pca', random_state=0), "t-SNE"),
              (PCA(n_components), "PCA"),
              (LDA(n_components=n_components), "LDA"),
              ]

for idx, (estimator_obj, estimator_name) in enumerate(estimators):
    # estimator_obj, estimator_name = estimator[0], estimator[1]
    t0 = time()
    if estimator_name=="LDA":
        Y = estimator_obj.fit_transform(X, (color).astype(int))
    else:
        Y = estimator_obj.fit_transform(X)
    t1 = time()
    print("%s: %.2g sec" % (estimator_name, t1 - t0))
    ax = fig.add_subplot(2, 5, 5+idx)
    plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
    plt.title("%s (%.2g sec)" % (estimator_name, t1 - t0))
    ax.xaxis.set_major_formatter(NullFormatter())
    ax.yaxis.set_major_formatter(NullFormatter())
    plt.axis('tight')
    
plt.show()

standard: 1.8 sec
ltsa: 79 sec
hessian: 2.2 sec
Isomap: 2.5 sec
MDS: 15 sec
Laplace Eigenmaps: 25 sec
t-SNE: 4.8 sec
PCA: 0.0012 sec
LDA: 0.0015 sec

左上角子图是原始维度中的样本，其他九个子图是降维后的二维效果，每个结果子图的标题中显示了该模型的训练时间。可以发现：

• 原始样本像是一条二维彩带，卷曲在三维空间中。
• 从结果看，PCA与 LDA表现类似。都是找到了一个最能体现样本之间差异的切面进行三维到二维的映射，但都无法达到“展开”嵌入在外围空间中流形的目的。
• MDS和流形学习模型都达到了“展开”彩带的效果，展开效果尤以LTSA、Hessian LLE、Isomap、t-SNE为佳。
• 从训练时间上看，PCA 最快，LDA 与其相近，之后是一众流形学习方法。因为需要计算所有样本的两两距离，MDS也很慢。但最慢的是t-SNE，耗时为倒数第二的MDS的十余倍，这是每个样本都需要拟合独立概率分布所致。

参考资料

• 局部线性嵌入(LLE)原理总结
• t-SNE原理与推导
• 流形学习 (Manifold Learning)
• Sklearn中文文档
• 从机器学习到深度学习
• 介绍一下流形学习的基本思想
• 流形学习(Manifold Learning)