【欧拉角、四元数】公式推导与互相转换

Know About Euler Angles and Quaternion

2023-5-28 14:59:43

Euler Angles

The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body with respect to a fixed coordinate system(Wikipedia). In classic Euler angles that a zero degrees represent the vertical orientation while in the alternative form introduced by Peter Guthrie Tait and George H. Bryan that zero degrees represent the horizontal position.

Three composed elemental rotations(rotations about the axes of a coordinates system) are sufficient to reach any target frame, and called as **extrinsic **if the rotation is with respect to the motionless original coordinate xyz, or **intrinsic **if the coordinate XYZ rotates with the moving body.

Euler angles are typically denoted as $\alpha$, $\beta$, $\gamma$ or $\psi$, $\theta$, $\phi$, depends. There are 12 different conventions for definition of the rotation axes:

Proper Euler angles: $(z-x-z,x-y-x,y-z-y,z-y-z,x-z-x,y-x-y)$

Tait-Bryan angles: $(x-y-z,y-z-x,z-x-y,x-z-y,z-y-x,y-x-z)$

Tait-Bryan angles are also called Cardan angles, nautical angles; heading, elevation, and bank; or yaw(bearing), pitch(elevation) and roll(bank). The line of nodes(N) is defined as the intersection of planes xy and XY or common perpendicular to the axes z and Z. Then the N can be written as $N=z\times Z$¹. The Euler angles can be defined as:

• $\alpha$(or $\psi$) is the signed angle between x and N(x-convention, or y-convention defined between y and N).

• $\beta$(or $\theta$) is the signed angle between z and Z axis.

• $\gamma$(or $\phi$) is the signed angle between the N and X axis(x-convention).

Angles follow the right-hand rule, which has positive values when representing a rotation clockwise.

Gimbal Lock: When two circular arms rotate on the same plane, for example: xy and the XY planes are identical(z axis and the Z axis have the same or opposite directions), as shown in the figure

The rotation sequence is hierarchical, therefore the upper-level rotation will change the direction of the axis in the lower level.

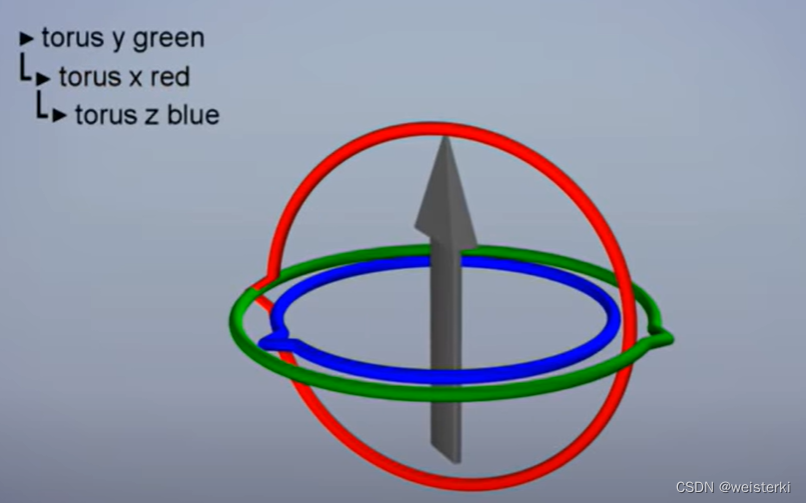
Now we can not turn the arrow down unless we rotate all axis in several steps. The solution of the gimbal is to change the rotation order, but just solve the problem temporarily, in where the gimbal changed direction. There are six combinations of gimbals, xyz, zxy, yxz, xzy, zyx and yzx.

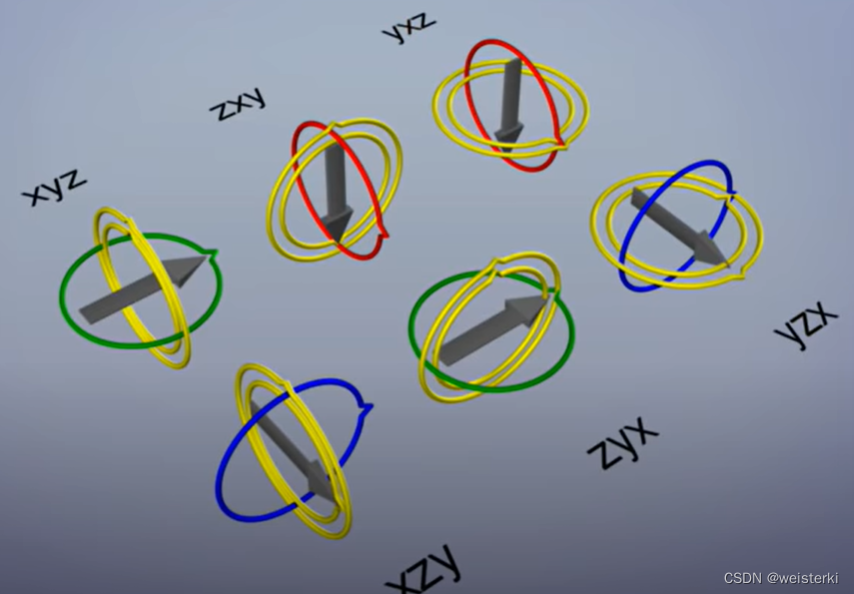
The best way to avoid gimbal is to find the least possible direction. Or, using quaternion.

Quaternion

Quaternions are generally represented in the form:
KaTeX parse error: Undefined control sequence: \label at position 12: a+bi+cj+dk\̲l̲a̲b̲e̲l̲{1}
where $a$, $b$, $c$ and $d$ are real numbers and $1$,$i$, $j$, and $k$ are the basis vectors or basis elements. Quaternions are used to avoid the gimbal lock in the Euler angle, because it can transform between Euler angles and rotation matrix². The quaternion satisfied those constraint:
$$\begin{gathered} i^2=j^2=k^2=-1 \\ ij=-ji=k \\ jk=-kj=i \\ ki=-ik=j \end{gathered}$$
We can rewrite the equation KaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{1} as the sum of scalar and vector:
$$q=a+bi+cj+dk=s+v$$
If $q_1=s_1+v_1$, $q_2=s_2+v_2$, then
KaTeX parse error: Undefined control sequence: \label at position 65: …+ v_1\times v_2\̲l̲a̲b̲e̲l̲{4}
If a quaternion $q=s+v$ and another quaternion $\tilde{q}=s-v$, then $\tilde{q}$ called conjugate quaternions. The product of a quaternion and its conjugate quaternion equals to the dot product of the quaternion itself, that is square of length of the quaternion.
$$q\tilde{q}=\tilde{q}q=q\bullet q={\left|q\right|}^2=q^2$$
The inverse of quaternion $q$ is $q^{-1}=\frac{\tilde{q}}{q^2}$, and $q{q}^{-1}=1$.

Reference

Scalar product(dot product) and vector product:

Let $A$ and $B$ be vectors, then the Scalar product is :

$$A\bullet B=\left|A\right|\left|B\right|\cos \theta$$
The result of the scalar product is a number, which means the length of $A$ project on $B$. The equation is derived from the law of cosines. While the result of a vector product is still the vector, and its module is:
$$\left|A\times B\right|=\left|A\right|\left|B\right|\sin \theta$$
Considering the direction and module:
KaTeX parse error: Expected 'EOF', got '&' at position 2: &̲ A\times B=det(…
which is a vector that perpendicular to the plane of $A$ and $B$, its length equals to the area of the rhomboid consist of $A$ and $B$.

Quaternion and rotation matrix

This deduce refer to those links:

Quaternion & rotation

如何推导旋转矩阵

From dot and vector product to rotation matrix

First of all, think about the coordinate of a point in the polar coordinates $x$ and $y$. Then they can be calculated from:
KaTeX parse error: Expected 'EOF', got '&' at position 2: &̲ x = r\cos\thet…
Ok. Now given two n dimensions’ vector $P$ and $Q$. As illustrated earlier, their dot product is:
$$P\bullet Q=\left|P\right|\left|Q\right|\cos \alpha$$
Where $\alpha$ is the angle between vectors.

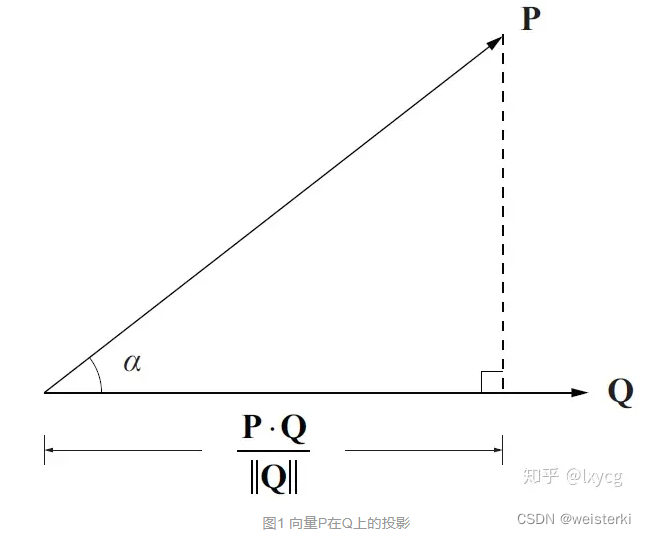
Therefore, the vector $P$ project on $Q$ (a vector, the result of dot product is a scalar, need to multiplied a unit vector)is:
KaTeX parse error: Undefined control sequence: \label at position 53: … \right |}^2 }Q\̲l̲a̲b̲e̲l̲{11}
Write as the matrix product(assume $P$ and $Q$ are column vectors):
KaTeX parse error: Undefined control sequence: \label at position 207: …z \end{bmatrix}\̲l̲a̲b̲e̲l̲{12}

The vector from $P$ perpendicular to $Q$ is:
$$pro{p}_{Q}P=P-pro{j}_{Q}P=P-\frac{P\bullet Q}{{\left|Q\right|}^2}Q$$
If $P$ and $Q$ are 3 dimensions, then their vector product is:
$$P\times Q=<P_y{Q}_z-P_z{Q}_y,P_z{Q}_x-P_x{Q}_z,P_x{Q}_y-P_y{Q}_x>$$
Write as matrix product:
KaTeX parse error: Undefined control sequence: \label at position 145: …z \end{bmatrix}\̲l̲a̲b̲e̲l̲{15}
Now we have a vector$P=<P_x,P_y>=<x,y>$, and rotate it 90${}^{\circ }$.

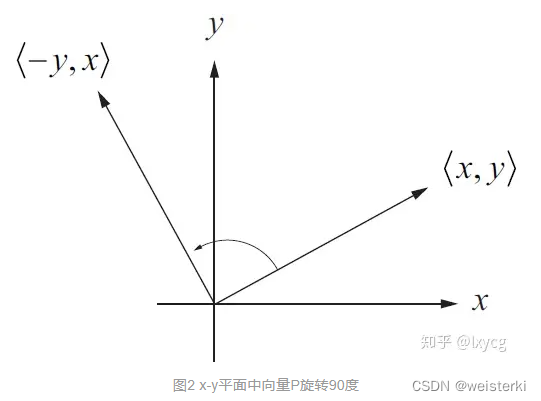
Then the rotated vector $Q=<-P_y,P_x>=<-y,x>$.

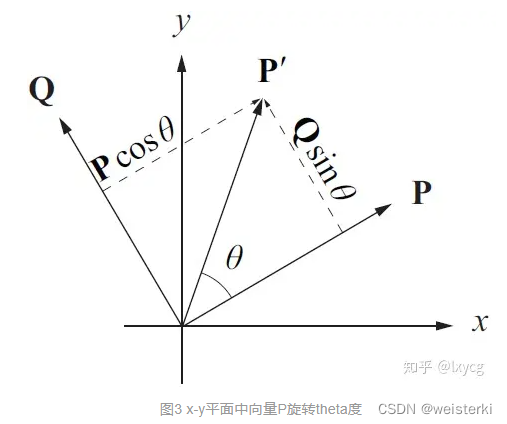
As shown in the figure, if $P^{\prime }$ is the vector after $P$ rotate $\theta$, then according to the polar coordinates illustrated in equation KaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{9}, the coordinates of $P^{\prime }$ is :
KaTeX parse error: Undefined control sequence: \label at position 29: …ta +Q\sin\theta\̲l̲a̲b̲e̲l̲{16}
Substitute $P$ and $Q$, then:
$$\begin{gathered} P_x^{\prime }=P_x\cos \theta -P_y\sin \theta \\ {P}_y^{\prime }=P_y\cos \theta +P_x\sin \theta \end{gathered}$$
That is:
$$P^{\prime }=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]P$$
This rotation matrix can be extended to 3 dimensions, if rotate about z axis for $\theta$ (just keeping the z coordinate same):
$$R_z(\theta )=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]$$
Similarly, the rotation matrix about x and y axis:

$$R_x(\theta )=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\theta & -\sin \theta \\ 0& \sin \theta & \cos \theta \end{array}\right]$$

$$R_x(\theta )=\left[\begin{array}{ccc}cos\theta & 0& \sin \theta \\ 0& 1& 0\\ -\sin \theta & 0& \cos \theta \end{array}\right]$$

Now we want to make the rotation matrix more generally, let $P$ rotates about axis $A$ for $\theta$, where $A$ is a unit vector. The projection $P$ to $A$ according to equationKaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{11}is:
$$pro{j}_{A}P=(A\bullet P)A$$
Similarly, the vector from $P$ perpendicular to $A$ is
$$pro{p}_{A}P=P-(A\bullet P)A$$

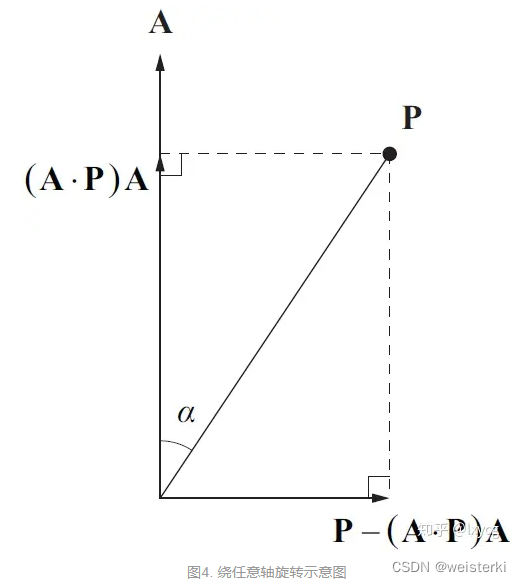
The vector after rotation consists of the projection on A axis and the vector $pro{p}_{A}P$ after rotation. Remind that the A is the rotation axis, therefore the projection $pro{j}_{A}P$ doesn’t change. As shown in the upper figure, the length of $pro{p}_{A}P$ is $\left|P\right|\sin \alpha$ . How to construct the rotated $P$ vector? We need a vector perpendicular to $A$ and $P$, combined with $pro{p}_{A}P$. This perpendicular vector could be obtained by vector product:$A\times P$. As shown in the figure, vector $A\times P$ and $pro{p}_{A}P$ construct a new coordinate. We should mind, because $A$ is unit vector, therefore the length of $A\times P$ is equal to $\left|P\right|\sin \alpha$, that is $pro{p}_{A}P$. Also, the length of $P^{\prime }$ also equals to $pro{p}_{A}P$, now the coordinate is actually same with equation KaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{16}

Therefore, the coordinate of rotated $pro{p}_{A}P$ is:

$$[P-(A\bullet P)A]\cos \theta +(A\times P)\sin \theta$$
Then the vector of rotated $P$ , $P^{\prime }$ is combination of $pro{j}_{A}P$ and rotated $pro{p}_{A}P$:
KaTeX parse error: Undefined control sequence: \label at position 139: …)(1-\cos\theta)\̲l̲a̲b̲e̲l̲{25}
According to equations KaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{12} and KaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{15}, substitute $A\times P$ and $(A\bullet P)A$ ($A$ is unit vector):
$$P^{\prime }=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]P\cos \theta +\left[\begin{array}{ccc}0& -A_z& A_y\\ A_z& 0& -A_x\\ -A_y& A_x& 0\end{array}\right]P\sin \theta +\left[\begin{array}{ccc}{A_x}^2& A_x{A}_y& A_x{A}_z\\ A_x{A}_y& {A_y}^2& A_y{A}_z\\ A_x{A}_z& A_y{A}_z& {A_z}^2\end{array}\right]P(1-\cos \theta )$$

Quaternion represents rotation

Assume the rotation in 3-dimension space is a function $\varphi$, to keep the vector’s length angle and handedness during rotation, this function should satisfy:
$$\begin{gathered} \left|\varphi (P)\right|=\left|P\right| \\ \varphi (P_1)\bullet \varphi (P_2)=P_1\bullet P_2 \\ \varphi (P_1)\times \varphi (P_2)=\varphi (P_1\times P_2) \end{gathered}$$
Also because $\varphi (s+v)=s+\varphi (v)$ (inner product space mapping to itself),
$$\varphi (P_1)\bullet \varphi (P_2)=\varphi (P_1\bullet P_2)$$
Therefore, according to equation KaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{4}, let $P$ be a quaternion with $s=0$, then
KaTeX parse error: Undefined control sequence: \label at position 132: … = \phi(P_1P_2)\̲l̲a̲b̲e̲l̲{29}
for both dot product and vector product. The function satisfied equation KaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{29} is called homomorphism.

Now we assume a function${\varphi }_q(P)=qP{q}^{-1}$ is a quaternion presentation of the rotation matrix. It can be proved that this function satisfied the rotation properties and also homomorphism. To be easy to prove, we assume $q=s+v$ is unit quaternion, its inverse is $q=s-v$. Give a vector $P$, we have
KaTeX parse error: Undefined control sequence: \label at position 74: …times P\times v\̲l̲a̲b̲e̲l̲{30}
according to theorem: Given two 3-D vector $P$, $Q$, then $P\times (Q\times P)=P\times Q\times P=P^{2}Q-(P\bullet Q)P$. Substitute into KaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{30} and let $v=tA$($A$ is unit vector as rotation axis), we have
$$qP{q}^{-1}=(s^2-t^2)P+2stA\times P+2t^2(A\bullet P)A$$
compare to equationKaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{25}, we can have
$$\begin{gathered} t=\sin \frac{\theta }{2} \\ s=\cos \frac{\theta }{2} \end{gathered}$$
Therefore, we find a quaternion $q$, which could construct the rotation matrix about axis $A$ for $\theta$:
$$\begin{gathered} q=s+v \\ =s+tA \\ =\cos \frac{\theta }{2}+A\sin \frac{\theta }{2} \end{gathered}$$
Now we could use a quaternion $q$ to rotate a vector $P$:
$$P^{\prime }=qP{q}^{-1}$$

Quaternion to rotation matrix

We write equation (31) to matrix according to dot product and vector product:
KaTeX parse error: Undefined control sequence: \label at position 350: … \end{bmatrix}P\̲l̲a̲b̲e̲l̲{35}
We rewrite $q=s+tA$ to quaternion $q=<w,x,y,z>$, where $w=s,x=t{A}_x,y=t{A}_y,z=t{A}_z$, and $x^2+y^2+z^2=t^2{A}^2=t^2$, now equation KaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{35}become:
$$qP{q}^{-1}=\left[\begin{array}{ccc}{w}^2-x^2-y^2-t^2& & \\ & w^2-x^2-y^2-t^2& \\ & & w^2-x^2-y^2-t^2\end{array}\right]P+\left[\begin{array}{ccc}0& -2wz& 2wy\\ 2wz& 0& -2wx\\ -2wy& 2wx& 0\end{array}\right]P+\left[\begin{array}{ccc}2x^2& 2t^2{A}_x{A}_y& 2xz\\ 2xy& 2y^2& 2yz\\ 2xy& 2yz& 2z^2\end{array}\right]P$$
also,
$$w^2-x^2-y^2-z^2=1-2x^2-2y^2-2z^2$$
Finally, according to equationKaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{38}, we can get rotation matrix:
KaTeX parse error: Undefined control sequence: \label at position 138: …2 \end{bmatrix}\̲l̲a̲b̲e̲l̲{38}
Now if we have the quaternion and rotation axis, we could get $w,x,y,z$, and $R_q$.

Rotation matrix to Quaternion

This deduce refer to 三维旋转：欧拉角、四元数、旋转矩阵、轴角之间的转换

If we have a rotation matrix, we should keep in mind a rotation matrix should be orthogonal. From equation KaTeX parse error: Undefined control sequence: \eqref at position 1: \̲e̲q̲r̲e̲f̲{38}, we know:
$$\begin{gathered} m_{32}-m_{23}=4xw \\ {m}_{13}-m_{31}=4yw \\ {m}_{21}-m_{12}=4zw \end{gathered}$$
also:
$$\begin{gathered} tr(R_q)=m_{11}+m_{22}+m_{33} \\ =3-4(x^2+y^2+z^2) \\ =4(1-(x^2+y^2+z^2))-1 \\ =4w^2-1 \end{gathered}$$
Therefore:
$$\begin{gathered} w=\frac{\sqrt{tr(R_q)+1}}{2} \\ x=\frac{m_{32}-m_{23}}{4w} \\ y=\frac{m_{13}-m_{31}}{4w} \\ z=\frac{m_{21}-m_{12}}{4w} \end{gathered}$$

Euler angles and rotation matrix

Euler angles to rotation matrix

**How to transform Euler angle to rotation matrix? Just multiply three elemental rotation matrices. **

Rotation matrix to Euler angle

For ZXY order(according to the yaw pitch roll angle range):

• Y axis yaw angle:

$$\alpha =atan2(m_{13},m_{33})$$

• Y axis pitch angle:

$$\beta =arcsin(-m_{23})$$

• Z axis roll angle:
  $$\gamma =atan2(m_{21},m_{22})$$

If gimbal lock occur, $m_{23}=-\sin \beta =\pm 1$, or $\cos \beta =0$ these equations become questionable. At the time, $\beta =\pm \frac{\pi }{2}$, the rotation matrix is:
$$R(\alpha ,\beta ,\gamma )=\left[\begin{array}{ccc}\cos (\alpha \pm \gamma )& \sin (\alpha \pm \gamma )& 0\\ 0& 0& \pm 1\\ -\sin (\alpha \pm \gamma )& -\cos (\alpha \pm \gamma )& 0\end{array}\right]$$
if $\beta =-\frac{\pi }{2}$,
$$\begin{gathered} R(\alpha ,\beta ,\gamma )=\left[\begin{array}{ccc}\cos (\alpha \pm \gamma )& \sin (\alpha \pm \gamma )& 0\\ 0& 0& 1\\ -\sin (\alpha \pm \gamma )& -\cos (\alpha \pm \gamma )& 0\end{array}\right] \\ \alpha +\gamma =atan2(-m_{12},m_{11}) \end{gathered}$$
if $\beta =\frac{\pi }{2}$,
$$\begin{gathered} R(\alpha ,\beta ,\gamma )=\left[\begin{array}{ccc}\cos (\alpha \pm \gamma )& \sin (\alpha \pm \gamma )& 0\\ 0& 0& -1\\ -\sin (\alpha \pm \gamma )& -\cos (\alpha \pm \gamma )& 0\end{array}\right] \\ \alpha -\gamma =atan2(m_{12},m_{11}) \end{gathered}$$
Give one value to $\alpha$ or $\gamma$ to calculate.

---

1. Background knowledge of vector’s product ↩︎

2. Quaternion and roatation matrix ↩︎