参考：
《一站式解决：隐马尔可夫模型（HMM）全过程推导及python代码实现》知乎
《Speech Recognition using Hidden Markov Model - DiVA》（硕士论文，推导细节可以参阅此文献）
《A Revealing Introduction to Hidden Markov Models》2021.4.12【重要文献，案例说明】
《A Hidden Markov Models》—隐马尔可夫模型-斯坦福大学
《Hidden Markov Models ——A lecture given by Tapas_Kanungo》
《A tutorial on hidden Markov models and selected applications in speech recognition》
《Mar隐马尔可夫模型（第3部分） 深入了解Hidden Markov Model 的训练理论》Medium文
《统计学习方法——（第十章）隐马尔科夫模型详解》（公式推导细节参考）
《Speech Recognition — GMM, HMM》
https://www.cnblogs.com/sddai/p/8475424.html
零、HMM发展大事记
1913
Russian mathematician A. A. Markov recognizes that in a sequence of random variables, one variable may not be independent of the previous variable. For example, two successive coin tosses are independent but today's weather might depend on yesterday's weather. He models this as a chain of linked events with probability assigned to each link. This technique later is named Markov Chain.
1966
Baum and Petrie at the Institute of Defense Analyses, Princeton, introduce the Hidden Markov Model (HMM), though this name is not used. They state the problem of estimating transition and emission probabilities from observations. They use maximum likelihood estimate.
1967
Andrew Viterbi publishes an algorithm to decode information at the receiver in a communication system. Later named Viterbi algorithm, it's directly applicable to the decoding problem in HMM. Vintsyuk first applies this algorithm to speech and language processing in 1968.
1970
The Baum-Welch algorithm is proposed to solve the learning problem in HMM. This algorithm is a special case of the Expectation-Maximization (EM) algorithm. However, the name HMM is not used in the paper and mathematicians refer to HMM as "probabilistic functions of Markov chains".
1975
James Baker at CMU applies HMM to speech recognition in the DRAGON speech understanding system. This is one of the earliest engineering applications of HMM. HMM is further applied to speech recognition through the 1970s and 1980s by Jelinek, Bahl and Mercer at IBM.
1989
Lawrence Rabiner publishes a tutorial on HMM covering theory, practice and applications. He notes that HMM originated in mathematics and was not widely read by engineers. Even when it was applied to speech processing in the 1970s, there were no tutorials to help translate theory into practice.
2003
HMM is typically used when the number of states is small but one research team applies it to large scale web traffic analysis. This involves hundreds of states and tens of millions of observations.
一、必要的数学知识
1.联合概率与边缘概率
联合概率是指多维随机变量中同时满足多个变量时候的概率，也就是共同发生的概率。A,B的联合概率通常写成 P(A∩B)或 P(AB)或 P(AB)。对于离散的变量，联合概率可以用表格形式表示或者求和表示，连续的变量可以使用积分表示（若是二维就一个二重积分）
边缘概率是指多维随机变量中只满足部分变量时的概率。图片帮助理解：
联合概率与边缘概率的关系：
边缘概率分布公式
联合概率的条件概率链式法则
举例：P(a,b,c)=P(a|b,c)*P(b,c）=P(a|b,c)*P(b|c)*P(c)
条件概率
独立性（XY相互独立）
P（X,Y）=P(X) *P(Y)
条件独立性
P（X,Y|Z）=P(X|Z)*P(Y|Z)
2.EM算法
关于EM算法利用jensen不等式近似实现极大似然估计的推导过程：https://zhuanlan.zhihu.com/p/36331115
二、隐马尔可夫模型（HMM）
1. 基本模型样式
上图中，白圈代表状态变量，蓝圈代表观测变量。所以白圈那一行是状态序列（隐状态），而白圈这一行是观测序列。
2. 模型的数学表达
HMM由隐含状态S、可观测状态O、初始状态概率矩阵π、隐含状态概率转移矩阵A、可观测值转移矩阵B（混淆矩阵）组成，可以使用一个三元组进行表述：
3. Markov两个假设
（1）齐次假设：表示 t 时刻的状态只与 t-1 时刻的状态有关
（2） 观测独立性假设：表示 t 时刻的观测变量只与 t 时刻的状态有关
4. 解决三个问题
（1）概率计算问题(Scoring / Evalution )：前向后向算法，已知模型 λ = (A, B, π)和观测序列O={o1, o2, o3 ...}，计算模型λ下观测O出现的概率P(O | λ)；【解决算法包括穷举搜索、向前算法(Forward Algorithm)、向后算法(Backward Algorithm)】
（2）学习问题（learning）：EM算法，已知观测序列O={o1, o2, o3 ...}，计算估计模型λ = (A, B, π)的参数即推断状态的转移情况，使得在该参数下该模型的观测序列P(O | λ)最大；【使用鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法)】
（3）预测问题（Decoding）：Viterbi算法，已知模型λ = (A, B, π)和观测序列O={o1, o2, o3 ...}，求给定观测序列条件概率P(I | O，λ)最大的状态序列 I；【使用维特比算法(Viterbi Algorithm)】
4.1 HMM模型的实质
HMM实际上就是建立建模 P(O,Q),【这里Q表示隐藏状态】对于给定的λ 进行建模：
4.2 关于转移矩阵A、B及π的定义
（1）状态转移矩阵A
根据Markov齐次假设去定义状态转移矩阵是一个NxN的矩阵，表示一个状态有N种可能性，前一个状态也有N种可能性。aij表示状态从前一个的 i 状态转变为现在的 j 状态的概率。
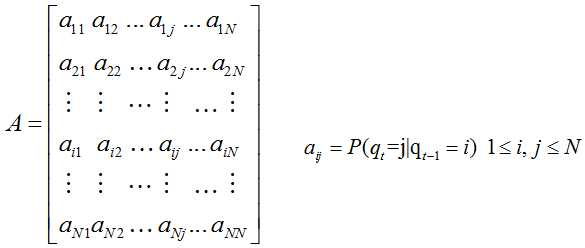
上述式中 q 表示状态，所以 qt 表示 t 时刻的转态。
（2）观测概率矩阵B（混淆矩阵）
根据Markov 观测独立性假设定义观测概率矩阵B是一个NxM的矩阵，表示对于N种状态，在这N种状态下对应的M个可观测变量的概率（比如说在晴天状态下，观测到的湿度、温度、风速等观测量的概率）。bj(k)表示 j 状态下的第 k 个观测量的 概率。
上式中P（ot=vk|it=qj）表示t 时刻状态为 qj 的情况下，t 时刻观察量为 vk的概率。
5.3 隐藏状态概率分布 π（t=1时刻的状态）
举例总结：
针对上述将的几个转移矩阵概念和初始状态π，举出一个盒子中摸球的例子帮助理解。
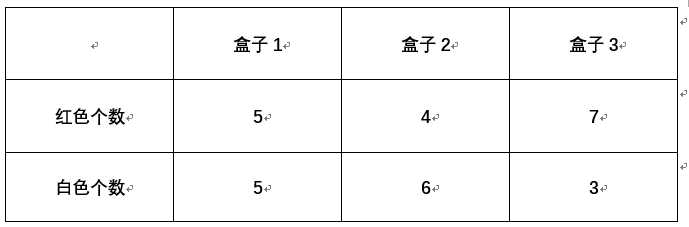
摸球规则：
开始的时候，从第一个盒子抽球的概率是0.2，从第二个盒子抽球的概率是0.4，从第三个盒子抽球的概率是0.4。以这个概率抽一次球后，将球放回。然后从当前盒子转移到下一个盒子进行抽球。规则是：如果当前抽球的盒子是第一个盒子，则以0.5的概率仍然留在第一个盒子继续抽球，以0.2的概率去第二个盒子抽球，以0.3的概率去第三个盒子抽球。如果当前抽球的盒子是第二个盒子，则以0.5的概率仍然留在第二个盒子继续抽球，以0.3的概率去第一个盒子抽球，以0.2的概率去第三个盒子抽球。如果当前抽球的盒子是第三个盒子，则以0.5的概率仍然留在第三个盒子继续抽球，以0.2的概率去第一个盒子抽球，以0.3的概率去第二个盒子抽球。
从紫色背景的摸球规则中，可以推断出初始矩阵：
从绿色背景的摸球规则中，可以推断出状态转移矩阵为
(矩阵的行列表示盒子123，数据表示转移概率)
从数据表格中可以推断出观测概率矩阵为：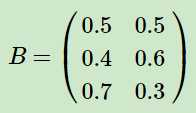
（矩阵的2列标识对应的观测结果，3行表示该观测结果下来自于不同盒子的概率）
【注】集合与序列的问题，集合不重复，所以这个案例中，观测集合为 {红，白}，状态集合为{盒子1，盒子2，盒子3}。所以M=2,N=3.但是观测序列可以是[红，白，红]等非2个元素的组成
4.3 概率计算问题及前后向算法
（1）概率计算问题定义：在给定模型 λ和观测序列O的情况下计算 P（O|λ）。【这里 I 表示隐藏状态】
（2）方法一：穷举法
思路：
- 列举所有可能的长度为T的状态序列I = {i1, i2, ..., iT}；每个i都有N个可能的取值。
- 求各个状态序列I与观测序列O的联合概率P(O,I|λ)；
- 所有可能的状态序列求和∑_I P(O,I|λ)得到P(O|λ)。
用到的公式：边缘概率公式 和条件概率的链式法则
P（O|λ）=ΣI P(O,I|λ) ←边缘概率公式
P(O,I|λ)= P(O|I, λ)P(I|λ) ←链式法则
第一步：
P(I|λ)= P(i1,i2, ..., iT |λ)
= P(i1 |λ)P(i2 | i1, λ)P(i3 | i2, λ)...P(iT | iT-1, λ) ←链式法则
上面的P(i1 |λ) 是初始为状态i1的概率，P(i2 | i1, λ) 是从状态 i1转移到 i2的概率，其他同理，于是分别使用初始概率分布π 和状态转移矩阵A，就得到结果：
∴
第二步：
P(O|I, λ) 在序列 I的条件下观测，所以
于是带入求和可得：
复杂度为：aij 的复杂度为NT，b的复杂度为 T，所以总的复杂度 O(TnT)。
对于此种算法，需要列举所以状态，这几乎是不可能的，而且有些问题中我们是无法知道所以状态的。即使可以，但是，计算量很大，是O(TNT)阶的，这种算法不可行。因此，有前向后向算法。
英文描述为：
（3）方法2：前向 / 后向算法（forward / backward algorithm）
解决概率计算(Scoring / Evalution )问题的另外两种快捷方法为：
a. 前向算法
b. 后向算法
I、 定义
前后向算法的区别之处：
在概念的定义上：
前向算法：当第t个时刻的状态为i时，前面的时刻分别观测到y1,y2, ..., yt的概率，即：
后向算法：当第t个时刻的状态为i时，后面的时刻分别观测到yt+1,yt+2, ..., yT的概率，即：
II、推导过程
前向算法推导过程：在给定模型 λ和观测序列O的情况下计算 P（O|λ）
在上面的粗暴概率计算中，复杂度大，所以我们可以使用递推公式来降低复杂度，于是在这里就是构造一个递推。
英文描述为：
附录：第2步的推导过程细节为：
后向算法类似于前向算法。
后向算法的英文描述为：
3.
附录： 第2步的推导过程细节为：
III、总结
4.4 学习问题及Baum Welch-EM算法
（1）学习问题定义
已知观测序列O={o1, o2, o3 ...}，计算估计模型λ = (A, B, π)的参数即推断状态的转移情况，使得在该参数下该模型的观测序列P(O | λ)最大。
即：
（2）算法思路
（3）Baum-Welch算法 (又称为forward-backward 算法)
首先回顾前向变量和后向变量两个概念：
| 前向变量 | 给定模型下，观察序列为 |
| 后向变量 | 给定模型下， |
再定义以下概念：
概念1：在给定观察序列下， 时刻从隐藏状态
转移到
的概率：
根据 和
可以计算得到联合概率分布：
进而可得到以下公式：
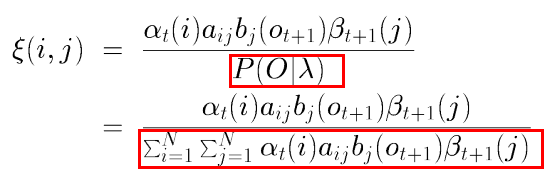
附录：
红色部分，即
的证明如下：
因为：
又因为：
所以结合下式，得证.
概念2：在给定观察序列下， 时刻隐藏状态为
的概率：
继续，
隐藏状态为 的数学期望，其实就是算平均值：
隐藏状态从 转移到
的数学期望(是
时刻为
,
时刻为
的联合概率)：
所以自然可以计算模型参数：
估算初始概率：
估算转移概率：
估算发射概率：
然后使用上边计算的估算值，替换初始的参数。反复进行迭代，直到得到局部最优解，即：
算法原理：
隐马尔可夫模型lamda = (pi, A, B)
- 定义评估方法，最大化可见状态链的前向概率alpha和后向概率beta
- 初始化模型参数：随机定义一套初始概率pi,转换概率矩阵A、输出概率矩阵B
- 不断的重复迭代
- E步：用当前的pi,A,B计算初alpha,beta(即前向算法-后向算法)
- M步： 用alpha和beta更新pi,A,B（贝叶斯理论公式基础）
- 重复上述步骤，当pi,A,B的更新区域静止时认为已经找到了模型的最佳参数，停止迭代
而我们知道，观测O由对应的状态决定，所以这里还隐含了状态这个未知变量，所以这个求解问题实际是一个隐变量求解问题，于是需要使用EM算法解决
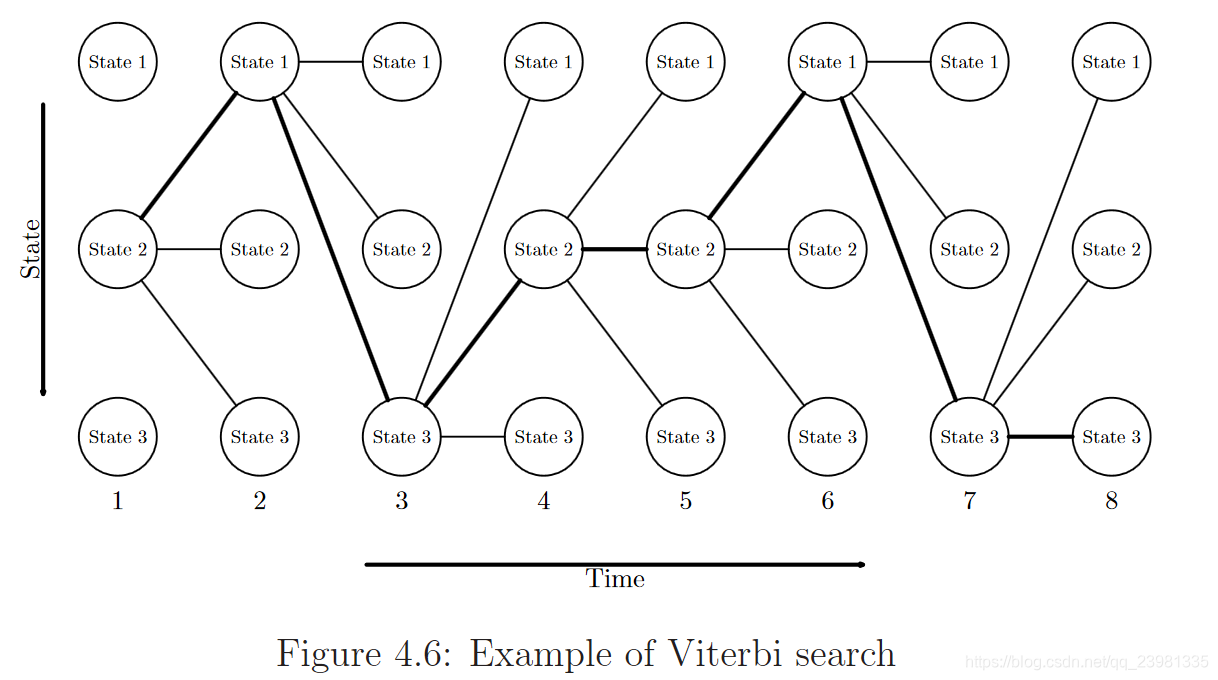
4.5 预测问题及Viterbi（维特比）算法
（1） 预测问题定义：
（2）思路分析
（3）常规Viterbi 算法
（4）改进的Viterbi 算法
三、案例及代码实现
本节主要参考：
《A Revealing Introduction to Hidden Markov Models》2021.4.12【重要文献，案例说明】
一个HMM模型所包含的要素如下：
- 隐藏状态
- 观测状态
- π向量：模型初始隐藏状态的概率
- 转移矩阵（A矩阵）：隐藏状态间转移的概率矩阵
- 混淆矩阵(也称发射概率矩阵， B矩阵)：隐藏状态与观察状态的对应概率矩阵
相关英语术语见下：
3.1 案例1及Code
案例1：小明现在有三天的假期，他为了打发时间，可以在每一天中选择三件事情来做，这三件事情分别是散步（Walk）、购物（Shop）、打扫卫生（Clean）(对应着可观测序列)，可是在生活中我们所做的决定一般都受到天气的影响，可能晴天的时候想要去购物或者散步，可能下雨天的时候不想出门，留在家里打扫卫生。而天气(晴天（Sunny）、下雨天(Rainy)就属于隐藏状态，用一幅概率图来表示这一马尔可夫过程：
根据案例可以得到：
T = don’t have any observation yet；
N = 2；
M = 3；
Q = {“Rainy”, “Sunny”}；
V = {“Walk”, “Shop”, “Clean”}
状态转移矩阵A为：
混淆矩阵B为：
初始隐藏状态的概率π为：
根据图中概率分布可以建立以下HMM模型：
states = ('Rainy', 'Sunny')
observations = ('walk', 'shop', 'clean')
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
transition_probability = {
'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
}
emission_probability = {
'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}
from hmmlearn import hmm
import numpy as np
model = MultinomialHMM(n_components=2)
model.startprob_ = np.array([0.6, 0.4])
model.transmat_ = np.array([[0.7, 0.3],
[0.4, 0.6]])
model.emissionprob_ = np.array([[0.1, 0.4, 0.5],
[0.6, 0.3, 0.1]])
现在，使用HMM可以解决哪些关键问题？
- 问题1 ，给定已知模型λ，序列O发生的可能性P（O|λ）是多少？【概率计算问题】
- 问题2 ，给定已知模型λ和序列O，最佳隐藏状态序列I是什么，即P（I |O，λ）？ 如果我们想知道天气是“下雨”还是“晴天”。【预测问题】
- 问题3 ，给定序列O和隐藏状态数，最大化O概率的最佳模型λ = (A, B, π)是什么，即计算估计模型λ = (A, B, π)的参数即推断状态的转移情况，使得在该参数下该模型的观测序列P(O | λ)最大？换句话说就是，我们要寻找的训练的目标是找到「 状态转移矩阵 A 」、「 观察转移矩阵 B 」、「 起始值转移矩阵 π 」【学习问题】
三种问题的具体计算推导公式见：
（1）《Hidden Markov models》（Centre for Vision Speech & Signal ProcessingUniversity of Surrey, Guildford GU2 7XH.）
（2）《A tutorial on hidden Markov models and selected applications in speech recognition》
（1）案例1的概率计算实例
import math
math.exp(model.score(np.array([[0]])))
# 0.30000000000000004
math.exp(model.score(np.array([[1]])))
# 0.36000000000000004
math.exp(model.score(np.array([[2]])))
# 0.3400000000000001
math.exp(model.score(np.array([[2,2,2]])))
# 0.04590400000000001比如，第二行代码，需要求出：第一个观测值O是“Walk”（对应为0）的概率，根据计算公式：
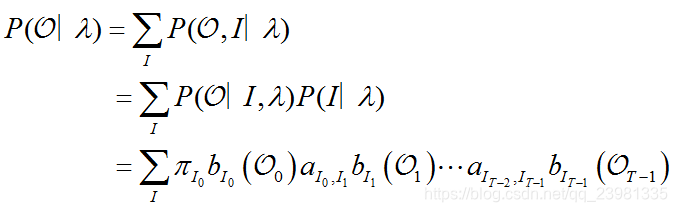
该概率等于初始状态分布π与发射概率矩阵B的乘积，
代码中通过调用.score提供计算的。
（2）案例1的预测（Decoding）问题实例
logprob, seq = model.decode(np.array([[1,2,0]]).transpose())
print(math.exp(logprob))
print(seq)
logprob, seq = model.decode(np.array([[2,2,2]]).transpose())
print(math.exp(logprob))
print(seq)输出结果为：
即：在已知模型λ和观测值={“Shop”，“Clean”，“Walk”}的情况下，最有可能的天气（隐藏状态）={“Rainy”，“Rainy”，“Sunny”}，概率约为1.5％。
给定已知的模型λ和观测值={“ Clean”，“ Clean”，“ Clean”}，最有可能的天气（隐藏状态）={“ Rainy”，“ Rainy”，“ Rainy”}，概率约为3.6％。
直观地讲，当“Walk”发生时，天气很可能不会是“Rainy”。
具体使用的方法（维特比算法(Viterbi)）及其步骤见《马尔科夫(Markov)》
（3）案例1的学习问题实例
3.2 案例2及代码实现
案例2：观察海藻湿度的状态，能否确定是雨天还是晴天。这个例子可能偏颇，需明确一下，海藻的湿度为可见状态，而天气状态为隐藏状态（假设盲人能够感知海藻湿度，却无法观察天气）。我们现定义海藻湿度分为四个等级为”dry”,”dryish”,”damp”,”soggy”.显而易见，不同的天气状况我们能观测到海藻不同湿度的概率是不同的，以表格的形式如下：
（1）案例2的概率计算问题及预测（Decoding）问题实例及代码
结合以上案例解决其概率计算问题的穷举搜索、递归思想之前向算法、后向算法，及解决其预测（Decoding）问题的Viterbi（维特比）算法具体推导及python代码（不使用HMM库，直接实现公式）实现见：
（2）案例2的学习问题实例及代码
隐马尔可夫模型的学习，根据训练数据是包括观测序列和对应的状态序列还是只有观测序列，可以分别由监督学习与非监督学习实现。以下文章首先介绍监督学习算法，而后介绍非监督学习算法——Baum-Welch算法（也就是EM算法），并用代码（不使用HMM库，直接实现公式）实现：
3.3 案例3及手撕代码
来源：书籍《Machine Learning：An Algorithmic Perspective》 CHAPTER16 Graphical Models 及其 code
参考：PPT《Hidden Markov Models and Eukaryotic Gene Finding》
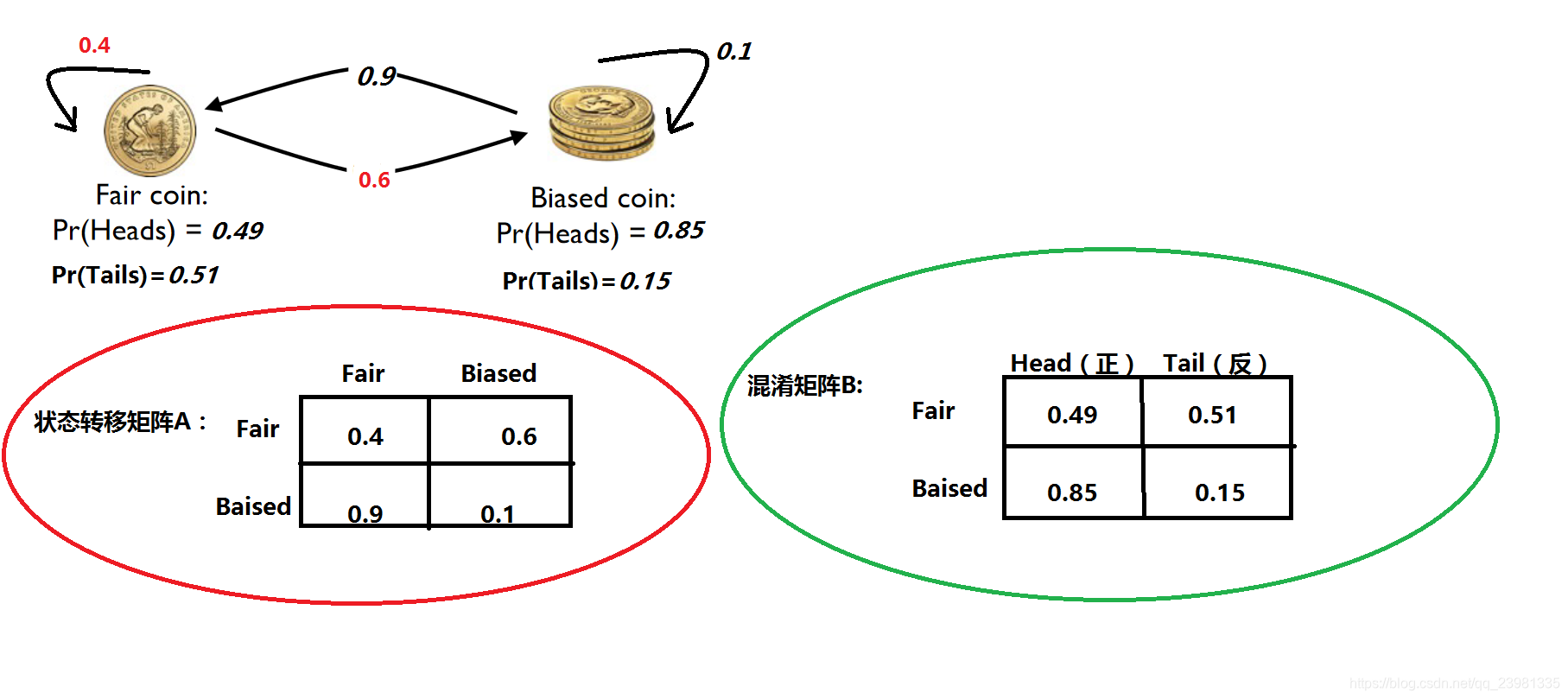
案例3：Suppose that you notice a fairground show where the showman demonstrates that a coin is fair, but then makes it turn up heads many times in a row. You notice that he actually has two coins, and swaps between them with sleight-of-hand. Watching, you start to see that he sticks to the fair coin（公平的硬币） with probability 0.4, and to the biased coin（偏币，有偏差的硬币）with probability 0.1, and that the biased coin seems to come up heads about 85% of the time. Make a hidden Markov model for this problem, construct an observation sequence, and use the Viterbi algorithm to estimate the states。
# Code from Chapter 16 of Machine Learning: An Algorithmic Perspective (2nd Edition)
# by Stephen Marsland (http://stephenmonika.net)
# You are free to use, change, or redistribute the code in any way you wish for
# non-commercial purposes, but please maintain the name of the original author.
# This code comes with no warranty of any kind.
# Stephen Marsland, 2008, 2014
# A basic Hidden Markov Model
import numpy as np
scaling = False
def HMMfwd(pi,a,b,obs):
nStates = np.shape(b)[0]
T = np.shape(obs)[0]
alpha = np.zeros((nStates,T))
alpha[:,0] = pi*b[:,obs[0]]
for t in range(1,T):
for s in range(nStates):
alpha[s,t] = b[s,obs[t]] * np.sum(alpha[:,t-1] * a[:,s])
c = np.ones((T))
if scaling:
for t in range(T):
c[t] = np.sum(alpha[:,t])
alpha[:,t] /= c[t]
return alpha,c
def HMMbwd(a,b,obs,c):
nStates = np.shape(b)[0]
T = np.shape(obs)[0]
beta = np.zeros((nStates,T))
beta[:,T-1] = 1.0 #aLast
for t in range(T-2,-1,-1):
for s in range(nStates):
beta[s,t] = np.sum(b[:,obs[t+1]] * beta[:,t+1] * a[s,:])
for t in range(T):
beta[:,t] /= c[t]
#beta[:,0] = b[:,obs[0]] * np.sum(beta[:,1] * pi)
return beta
def Viterbi(pi,a,b,obs):
nStates = np.shape(b)[0]
T = np.shape(obs)[0]
path = np.zeros(T)
delta = np.zeros((nStates,T))
phi = np.zeros((nStates,T))
delta[:,0] = pi * b[:,obs[0]]
phi[:,0] = 0
for t in range(1,T):
for s in range(nStates):
delta[s,t] = np.max(delta[:,t-1]*a[:,s])*b[s,obs[t]]
phi[s,t] = np.argmax(delta[:,t-1]*a[:,s])
path[T-1] = np.argmax(delta[:,T-1])
for t in range(T-2,-1,-1):
path[t] = phi[path[t+1],t+1]
return path,delta, phi
def BaumWelch(obs,nStates):
T = np.shape(obs)[0]
xi = np.zeros((nStates,nStates,T))
# Initialise pi, a, b randomly
pi = 1./nStates*np.ones((nStates))
a = np.random.rand(nStates,nStates)
b = np.random.rand(nStates,np.max(obs)+1)
tol = 1e-5
error = tol+1
maxits = 100
nits = 0
while ((error > tol) & (nits < maxits)):
nits += 1
oldpi = pi.copy()
olda = a.copy()
oldb = b.copy()
# E step
alpha,c = HMMfwd(pi,a,b,obs)
beta = HMMbwd(a,b,obs,c)
for t in range(T-1):
for i in range(nStates):
for j in range(nStates):
xi[i,j,t] = alpha[i,t]*a[i,j]*b[j,obs[t+1]]*beta[j,t+1]
xi[:,:,t] /= np.sum(xi[:,:,t])
# The last step has no b, beta in
for i in range(nStates):
for j in range(nStates):
xi[i,j,T-1] = alpha[i,T-1]*a[i,j]
xi[:,:,T-1] /= np.sum(xi[:,:,T-1])
# M step
for i in range(nStates):
pi[i] = np.sum(xi[i,:,0])
for j in range(nStates):
a[i,j] = np.sum(xi[i,j,:T-1])/np.sum(xi[i,:,:T-1])
for k in range(max(obs)):
found = (obs==k).nonzero()
b[i,k] = np.sum(xi[i,:,found])/np.sum(xi[i,:,:])
error = (np.abs(a-olda)).max() + (np.abs(b-oldb)).max()
print nits, error, 1./np.sum(1./c), np.sum(alpha[:,T-1])
return pi, a, b
def evenings():
pi = np.array([0.25, 0.25, 0.25, 0.25])
a = np.array([[0.05,0.7, 0.05, 0.2],[0.1,0.4,0.3,0.2],[0.1,0.6,0.05,0.25],[0.25,0.3,0.4,0.05]])
b = np.array([[0.3,0.4,0.2,0.1],[0.2,0.1,0.2,0.5],[0.4,0.2,0.1,0.3],[0.3,0.05,0.3,0.35]])
obs = np.array([3,1,1,3,0,3,3,3,1,1,0,2,2])
print Viterbi(pi,a,b,obs)[0]
alpha,c = HMMfwd(pi,a,b,obs)
print np.sum(alpha[:,-1])
def test():
np.random.seed(4)
pi = np.array([0.25,0.25,0.25,0.25])
aLast = np.array([0.25,0.25,0.25,0.25])
#a = np.array([[.7,.3],[.4,.6]] )
a = np.array([[.4,.3,.1,.2],[.6,.05,.1,.25],[.7,.05,.05,.2],[.3,.4,.25,.05]])
#b = np.array([[.2,.4,.4],[.5,.4,.1]] )
b = np.array([[.2,.1,.2,.5],[.4,.2,.1,.3],[.3,.4,.2,.1],[.3,.05,.3,.35]])
obs = np.array([0,0,3,1,1,2,1,3])
#obs = np.array([2,0,2])
HMMfwd(pi,a,b,obs)
Viterbi(pi,a,b,obs)
print BaumWelch(obs,4)
def biased_coins():
a = np.array([[0.4,0.6],[0.9,0.1]])
b = np.array([[0.49,0.51],[0.85,0.15]])
pi = np.array([0.5,0.5])
obs = np.array([0,1,1,0,1,1,0,0,1,1,0,1,1,1,0,0,1,0,0,1,1,0,1,1,1,1,0,1,0,0,1,0,1,0,0,1,1,1,0])
print Viterbi(pi,a,b,obs)[0]
print BaumWelch(obs,2)3.4 案例4
原文：《Mar隐马尔可夫模型（1、2、3部分）》
现有三间大型卖场在AIA 附近，分别是Costco、爱买、大润发，已知顾客今日在各个卖场间流动的固定机率(invariant)，亦即图上的数字，值得注意的是，从每间卖场画出去箭头上的数字相加起来为1 (ex: Costco 0.7+0.2+1 = 1)。 接着来看一下范例吧…今天刚来AIA报到的学员圆仔，每天都有一定的机率到某间卖场里购物，同时也会有某个机率在该间卖场买瓶饮料。在起始机率分别为0.5、0.1、0.4下，圆仔三天来逛卖场的顺序为 I (爱买, Costco,大润发) ，每到一间卖场他都会买一瓶饮料，三天来分别买了 O (雪碧,可乐,绿茶) 。该案例中，隐藏状态为 I (爱买, Costco,大润发)，可观测状态为： O (雪碧,可乐,绿茶) 。
（1）引入1：请问发生 I 和 O 的共同机率为多少呢？
答：请问发生 I 和 O 的共同机率，即求P(O，I)。由于：
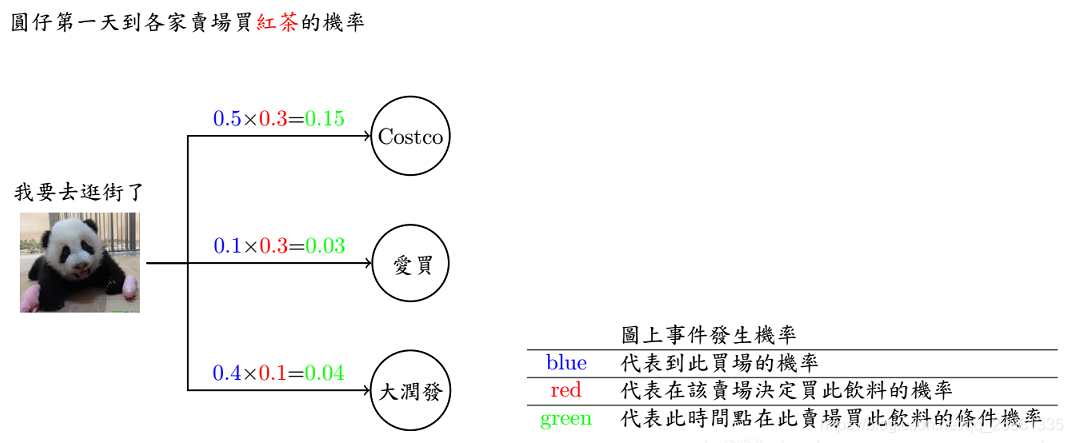
（2）引入2：现在换个问题来想想，如果已知连续三天到卖场买的饮料依序为 O (红茶,雪碧,绿茶)，请问有几种可能路线呢？ 每条路线分别发生的机率又有多少呢？
答案：已知模型 λ = (A, B, π)和观测序列O={o1, o2, o3， ...}，求总共几种可能路线，即求观测序列O在各个状态序列 I 下的条件概率P(O|I，λ)，可以用穷举法，即列举所有隐藏状态I =（I0，I1, I2）下[3x3x3=29种组合] 发生观测状态的概率。
（3）HMM 三大问题
第二个例子说明了，当只知观察值，而状态被隐藏的时候，如何找出「最佳的路径」。 但是，既然是model 一定是需要训练的，到底什么东西是需要被训练的呢？
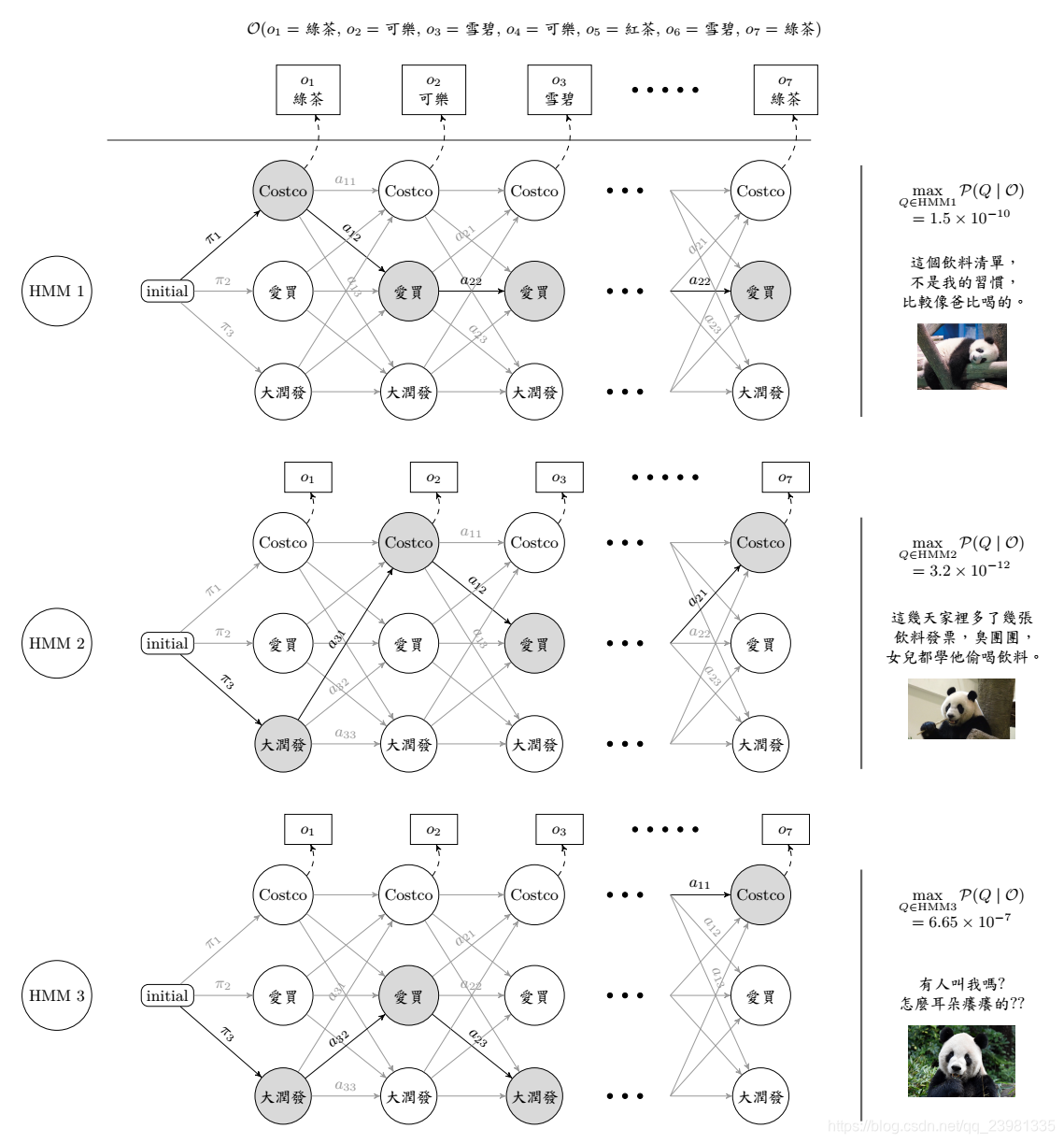
在实际遇到的问题中，我们并不会知道「机率转移矩阵」实际的机率是多少，换句话说，我们不知道上述所指的「转移矩阵A」和「混淆矩阵B」，只会有一堆数据。在此，我们用已知的转移矩阵条件下，举一个实际的分类问题，熊猫团团、圆圆、圆仔，半年来，每周买饮料（ 观察值）的依序清单，至于可能的路线，及多少机率会买到对应的饮料，皆是未知，根据个别的买卖习惯分析，训练对应的模型，找出对应的「转移矩阵A」和「混淆矩阵B」，最后我们要预测，当随便给一周的饮料的清单，最有可能是哪只熊猫的喜好。
（上图为HMM，其中一种方法，目的是算出在指定事件的发生状态下，算出此事件发生的最大机率之路径 )
HMM 三大问题：
A. 概率计算问题——向前-向后算法 （Forward-backward Algorithm）
B . 解码（预测）问题——维特比算法
C. 学习问题——使用鲍姆-韦尔奇算法(Baum-Welch Algorithm) (约等于EM算法）
D. (补充) Continuous Hidden Markov Chain
在进入主题前，再重申一次问题，如下图：
我们需计算在已知观察序列 O(o₁, o₂, o₃, …, ot) ，但未知转移矩阵A 和B的条件下，找出其对应的的所有可能状态序列 Q(q₁, q₂, q₃, …, qt ) ， 以及其中最大概率之状态序列Q(q₁, q₂, q₃, …, qt ) 。
有些人大概觉得简单吧！ 暴力法就可以解决了，穷举出所有可能的路径，并计算每条路径的机率，不就结束了吗？ 就是每条路径都算过，痾....时间复杂度是O(N^TT)呀！ 大大，在文明的21世纪，我们不能这么暴力呀！
以下的演算法要跟大家介绍，如何降低计算的时间复杂度。
（a）概率计算问题——前向-后向算法
forward 顾名思义，就是由前往后找路径，直到第 t 秒，其实也不太难，看到上图蓝色经过的流程图在这边forward要计算的部分只有 αt(j) ，意思就是在第 t 秒、第 j 个状态，发生 ot 的所有可能路径机率之加总值，所以只算第 t 秒和第 t 秒以前发生的可能路径机率！
backward 用膝盖想，就是由后往前算嘛，看看流程图之绿色部分， βt(j) 从第 t 秒开始，考虑由第 j 个状态出发，直至第 T 秒结束的所有路径机率之总和，由于不知道在 t 由 j 状态出发的机率值，所以我们是从已知第 T 秒发生的机率值，往前回推至第 t 秒的路径机率。
用图示法来看，不严谨的说法是forward乘上backward ，就恰巧是在观察序列 O 时，发生第 t 秒，经过第 j 个状态的所有可能路径机率之总和。
疑？ forward 往后算到底，不就是backward 往前算到底的值嘛？ 恩，是的，所以要估算路径机率，其实只要算一种就可以了。
何以利吾身？ 这样算有什么好处呢？ 时间复杂度大大的减少了呀！ 只剩下O(N²T) 唷！ 时间就是金钱，颗颗….不过这个演算法既然有forward 和backward，算这两个一定有原因呀！ 等等在底下会提到。
（b）预测（解码）问题— 维特比算法
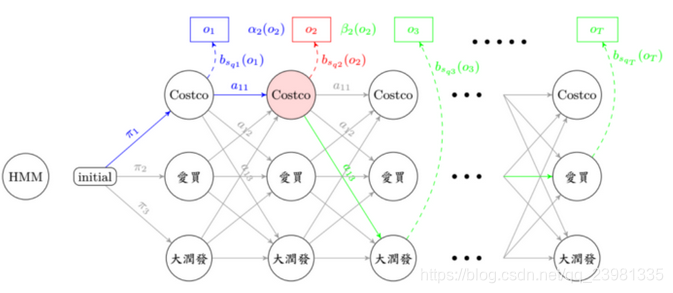
看到这边，应该都是会心一笑，其实和上个演算法差不多嘛！ 只是把∑变成max而已呀！ 是的，你没有看错就是这么简单，有别于上个演算法是要找出在第 t 秒，会经过第 j 个状态的所有可能路径机率总和，而这个演算法想表示的是，在第 t 秒，会经过第 j 个状态之最大机率路径。
（c）学习问题——EM算法
学习问题，学习要学什么呢？以上面例子为例，过去一年来，我们以周为一个观察序列单位，纪录圆仔每天买饮料的习惯，因此我们想从圆仔的饮料习惯纪录中，分析出「选择买什么东西」、「去哪间卖场购买的」，可惜的是，我们没有纪录到圆仔去哪间卖场买东西的诱因，亦即是「机率」，再换句话说，我们要寻找的训练的目标是找到「 状态转移矩阵 A 」、「 观察转移矩阵 B 」、「 起始值转移矩阵 π 」，而「圆仔的饮料习惯纪录」是我们的训练资料集。
了解问题之后，先来看一下离散问题的数学式，首先只考虑一周的饮料清单，透过 Forward-Backward Algorithm 我们可以求出αₜ(i)和βₜ(i)，也就是把每一个时间点会经过每一个状态及事件的所有可能路径机率都算出来，求出来之后，自然就要开始训练参数啦！
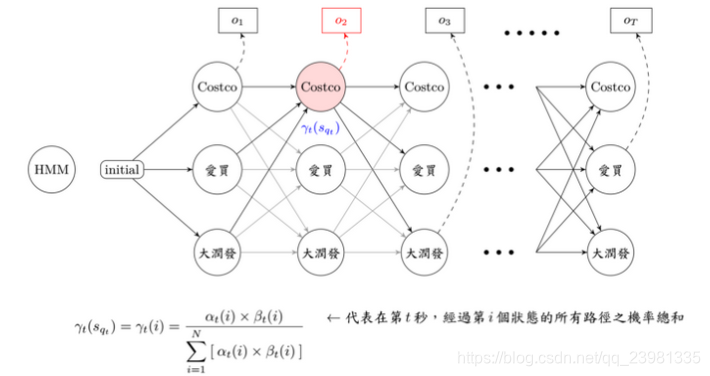
开始训练喽！
在标题中看到 EM Algorithm ，应该很快就联想到了「聚类」、「数据分布」，是的，我们这里处理的手法其实也差不多啦！ 利用事件发生的平均机率，当作更新的转移矩阵，接着反复的寻找和更新，直到更新幅度很小这样。
评论：
- 没有出现在资料集中的观察值，在更新的过程中，会被更新为0，一旦变成0，此事件路径发生的可能性即为0，因此不论计算Evaluate Problem 或是Decording Problem 此路径机率皆恒为0，意思是不会再更新，所以通常不会让没出现过的观察值机率为0，常理来说，会预设一个比0 大，但很小的数字。 只有离散问题，会遇到此状况，连续则无。
- 因为每次的update，都只与当下计算的观察序列有关，因此很容易看到第n 个序列的时候，就忘掉一开始看到的几个序列的样子了，为了避免这样的状况产生，所以我们让每次要更新的值，与将要被更新的值取一个比例平衡，既不忘了过去的观察序列，也不会全然依照新的观察序列更新，常用的方式如底下公式：
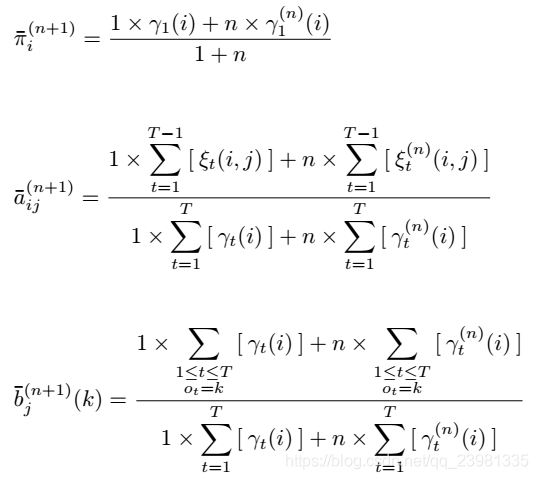
当然有些人会困惑，之前我们讨论的内容中，每个状态都会有固定对应的M个观察值，意思是，原先卖场饮料都是一罐一罐卖的，后来为了环保考量不用铝罐装，用一袋袋饮料装？ 由于是一袋袋的，所以每一袋饮料的重量都有些许的误差，长久下来，观察值会由消费者买了架上第k种每瓶为 L ml的饮料，变成是买了架上第k种每袋为 L ml的饮料，因为不是每袋都能很准确的装刚好 L ml的饮料，所以会有一点点偏差— 「连续型隐藏式马可夫模型Continuous Hidden Markov Model」
（d） (补充) Continuous Hidden Markov Model
上述的想法，大家思考一下，看到「 bias 偏差」大家会想到啥？ 八九不离十，是令人脑昏的「统计」，统计数据会想到啥？ 「常态分布Normal Distribution」。 没错，不管什么状态，未看先猜有「常态分布」，先对一半。 那什么东西训练中会与「常态分布」有关，眼睛闭着，也猜得到「 EM Algorithm 」，接着联想到的就是「 Gaussian Distribution 」、「 Gaussian Mixture Model 」。 既然有这些联想，那一切就好办了。 让我们走下去….
于是乎我们训练的目标中多了一个参数—在「状态 st 」产生「观察值 ot 」的机率。 目前我们以 Gaussian Mixture Model 为假设观察值 ot 所属分布，那马上就会想到，多了的训练参数是谁了吧!!!没错，就是「平均数mean μ」和「协方差covariance Σ」。
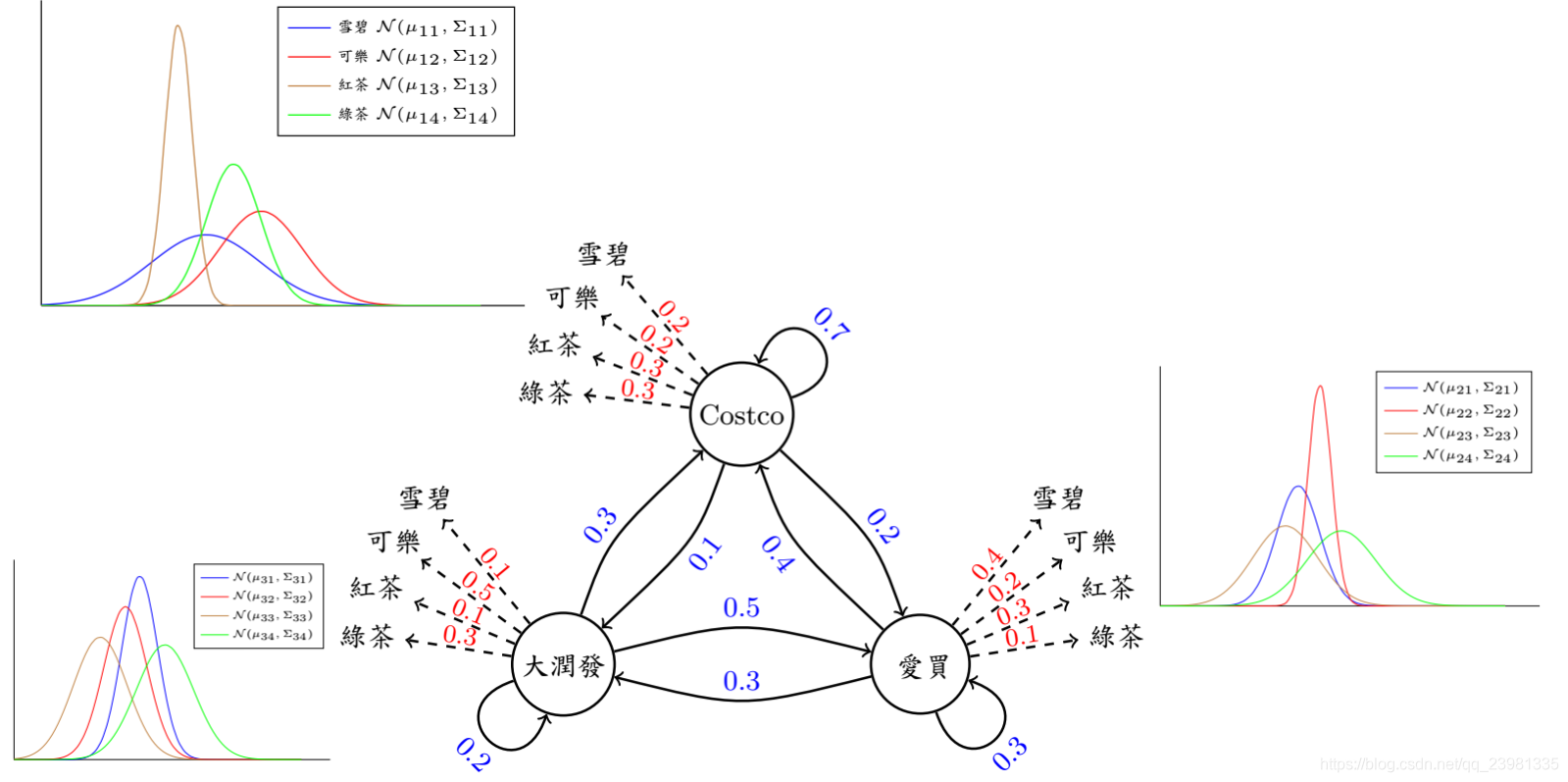
有了这张图，大概就清楚明了了吧！ 简单叙述整个问题，就是….圆仔每天都会去买饮料，所以我们纪录她每天买的饮料品项和饮料重量，然后每7天为一笔资料，目的是找出圆仔买东西的习惯和路径，以及买到东西多寡的分析，所以影响的因素和对应的名词有三个「卖场→状态」、「饮料→观察」、「饮料重量→ N( μ, Σ ) 」，目标是从这三者中计算出最可能是圆仔的习惯— —买东西的路径机率、选择买哪种饮料的机率、得到此饮料重量的机率。
一定会有人觉得紧张该怎么办，其实也不用怎么办啦!!!跟刚刚计算的方法差不多，只是多了要更新「平均值 μ 」和「协方差 Σ 」而已。
YA！ 我们终于结束Hidden Markov Model 系列啦!!!给自己一个欢呼吧！ 其实一切都不难，不要看到数学是就害怕了啦啦啦~~~~
扫一扫
177
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
