记录一下自己的推导过程,但不知道结果是否正确

同理,对于圆截面的直肋,则有如下计算:
题目:
解答:
首先有
,
,
是圆截面的周长,因此有
,然后因为单圆柱的体积为
,设有
个圆柱体,因此体积
,也就是说,总体积正比于
,利用这个性质,取
,因此有
,将以上式子代入
,得到
,整理后有:
,根据题意,
、
、
均为常数,过余温度
也是常数,因此为使圆截面直肋的直径
达到最佳,应该求
对
的倒数,并让导数
。
,其中
,
,根据复合函数求导定义有,
,令
,进一步化简有:
,提取公因子
有:
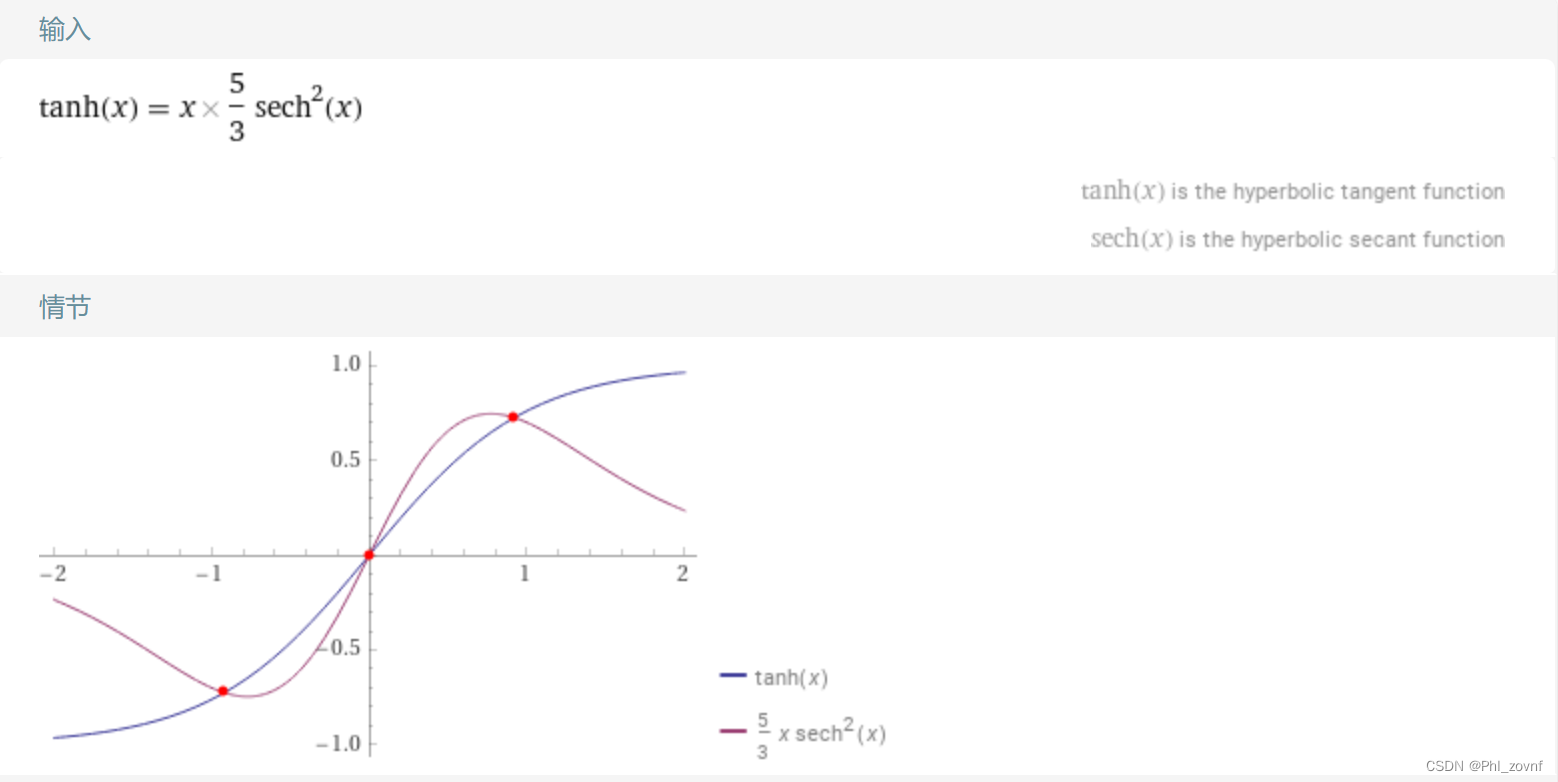
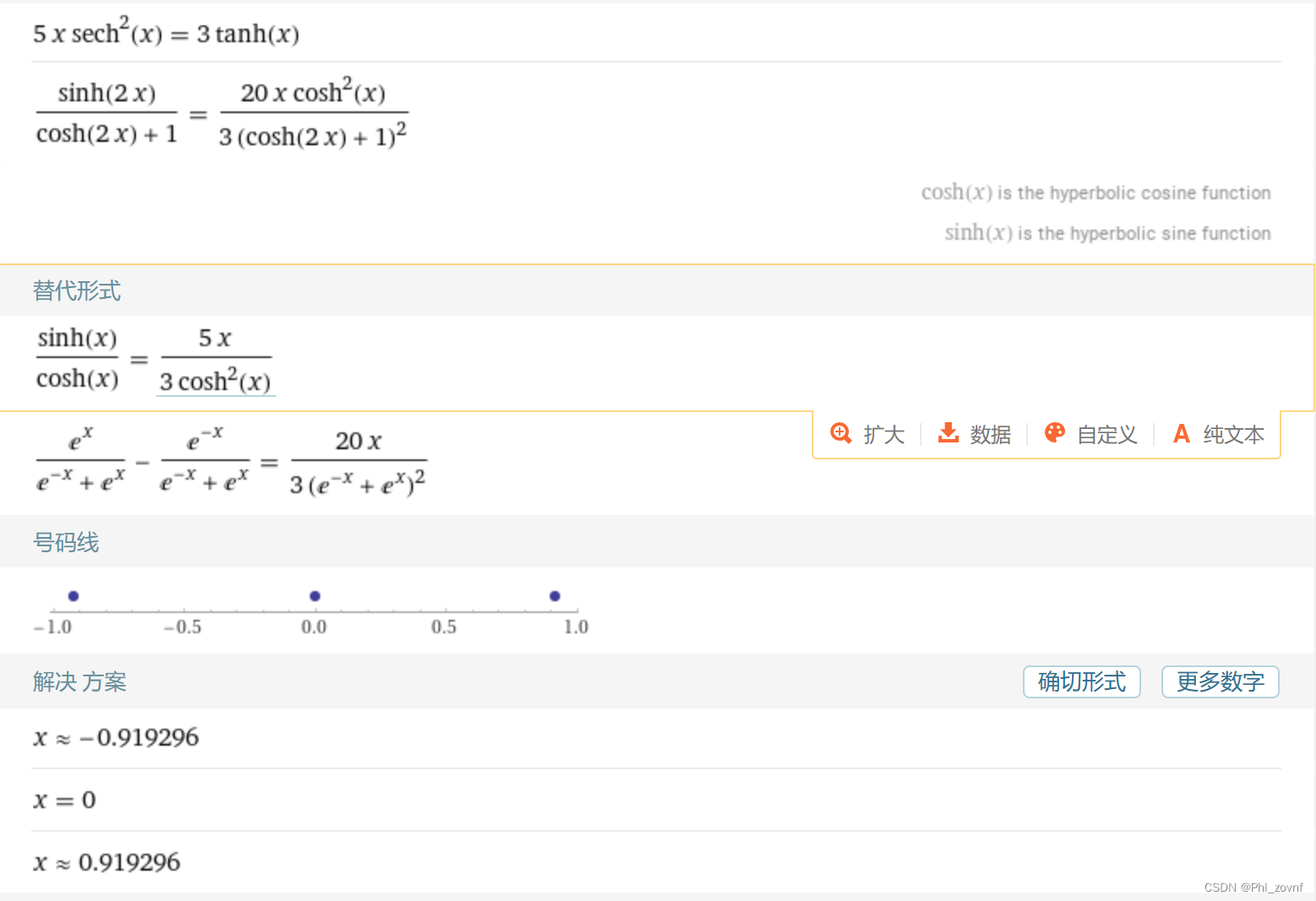
,移项后得到:
,用WolframAlpha网站,解上述方程,得到取正值的
。将该
和
代入式子
,得到最佳直径为
。当然,可以不展开
,这样就得到
,当知道总金属消耗量
,确定圆截面直肋数量
,从而知道
,代入上式子,得到最佳直径
,再算出高度
。

























 651
651











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








