浅谈传热学中温度分布曲线的凹凸分析

传热学主要研究的是热的传递问题，通常要求能掌握物体的温度分布，如何快速地判断一个温度曲线的凹凸性，是一项建议掌握的技巧。本文将从通过几个具体案例分析向大家介绍方法。

1、巧用傅里叶定律

傅里叶导热定律是最基本的描述热的方程，看似简单，使用它便能最迅速地判断出来。（大于）

  (1)变化的截面：圆柱导热对数曲线

  圆柱导热是经典的变截面A(x)问题。首先，假设>，通过圆柱的热流量Φ大小恒定，圆柱的半径由内向外增大，所以侧表面积A增大，λ是定值， 可推导出下降，我们可以微分化处理，那么表示曲线的斜率，斜率随着半径的增大而减小，可以判断是①曲线

 （2）变化的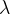

λ是导热系数，一般工程计算中为了简化计算，我们将它看做常数。实际上，也存在变导热系数的情况。

 对于的情形，分析如下：

①曲线：随着x横坐标的增大，减小，热流量不变，由傅里叶导热定律得，λ随x的增大而增大，又t随x的增大而减小，所以λ随t的增大而减小                         故b<0

② 曲线：随着x横坐标的增大，不变，热流量不变，由傅里叶导热定律得，λ随x的增大恒定不变，λ是定值                                                                               故b=0

③曲线：随着x横坐标的增大，增大，热流量不变，由傅里叶导热定律得，λ随x的增大而减小，又t随x的增大而减小，所以λ随t的增大而增大                         故b>0

  (3)变截面问题

如图所示，是一个圆台，左端面温度为，右端面温度为，其他为绝热条件，右侧是它的等温线。 大家有没有考虑过，为什么等温线是向左侧突出的弧形？为什么在右侧的等温线更密？使用傅里叶定律我们变可以解答，分析如下：

随着x的增大，截面积A减小，λ和Φ不变，所以增大,假设,我们可以得到温度变化的大致图像

 等温线越密的地方，温度变化越快，因此，我们知道右侧等温线更密集。

对于该圆台传热，任取过轴线的截面分析，可以画成三个部分，我们可以看作是并联的三块热阻，如下图所示：

 在同一与轴线垂直的截面上，Ⅱ部分的温度总是低于Ⅰ、Ⅲ部分的，所以曲线向左突起。

2、利用温度解析式

如果可以直接得到温度解析式，那么可以通过解析式直接判断曲线的凹凸性。例如肋的曲线分布。

肋的温度解析式为

对过余温度求导，有

对于双曲正弦函数shx的变化趋势大致为

 由图可知，随着x的增大，也增大。又x-H<0，随着x的增大，x-H也增大，增大但是,所以减小，肋片温度分布示意图为

 注：本文案例来源于13.2.6 典型一维稳态导热分析解举例（下）通过圆筒壁及球壳的导热(P13)_哔哩哔哩_bilibili

以及王秋旺老师的《传热学：重点难点及典型题精解》

 思路全为作者独立创作，如有雷同，纯属巧合。

部分图片来源百度，侵删。