摘要
传统的“elastic band”方法在规避障碍物的同时,会根据距离最短的原则修正全局路径规划算法生成的路径。不过“elastic band”方法没有考虑到机器人的任何运动学约束。本文提出了一种称为“Time elastic band”的方法,明确地考虑了运动在时间方面的动态约束,如有限的机器人速度和加速度。“Time elastic band”的求解是加权多目标优化框架中进行的。大多数目标都是局部的,因为它们只依赖于几个邻近的中间状态。这导致了系统矩阵非常的稀疏,使得在大规模约束下基于最小二乘法进行优化成为可能。
仿真和实际机器人的实验结果表明,该方法鲁棒性强,计算效率高,能够实时生成最优机器人轨迹。“Time elastic band”将一系列由路径点组成的初始路径转化为一条显式依赖于时间的轨迹,实现了对机器人的实时控制。由于该方法的模块化构成,使得其能够很容易扩展为包含有更多的目标和约束。
1 简介
运动规划是指找到一条符合运动学和动力学约束的没有碰撞轨迹。
在运动规划的背景下,本文着重于局部路径规划,并假设初始路径已经由全局规划器生成【1】。特别是在服务机器人的工作环境中,由于环境可能是动态的,具有内在的不确定性,因此局部路径规划是一种较好的方法。此外,环境模型可能会因局部、不完整的地图和动态障碍物而发生变化。此外,大规模全局路径的(重新)计算在实时应用中通常是不可行的。这导致了局部路径规划方法的出现,如文献【2,3】提出的“elastic band”。“elastic band”的主要思想是修正初始路径,将其视为一个受内外力平衡的弹性橡皮筋,在保持与障碍物的距离的同时,尽可能的绷紧路径。
随后,该方法被推广到non-holonomic 运动学【4,5、6】、多自由度机器人系统【7】和动态障碍【8】。然而,据我们所知,动力学约束尚未被认定是路径修正的一个目标。传统的方法是对路径进行平滑处理,例如使用样条曲线来获得动力学可行的轨迹。

我们提出了一种称为“timed elastic band”的新颖方法,由于它明确地给“elastic band”增加了时间信息,因而允许考虑机器人的动力学约束和直接修正轨迹而不是路径。图1显示了具有“timed elastic band”的机器人系统架构。通过考虑时间信息,“Timed elastic band”还可以用来控制机器人的速度和加速度。尽管本文考虑的是在平面环境中运动具有三个全局自由度和两个局部自由度的差分驱动移动机器人,但新方法也适用于高维状态空间。
2 Time Elastic Band
经典的“elastic band”使用n个机器人的中间位姿 的序列来描述,在下文中表示为包括了机器人在相关帧({地图}, 图2)中的位置
,
和方位角
的“configuration”:
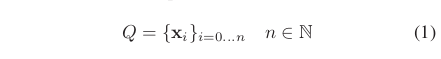
“timed elastic band”在两个连续“configuration”之间的增加了时间间隔,产生n−1个时差:

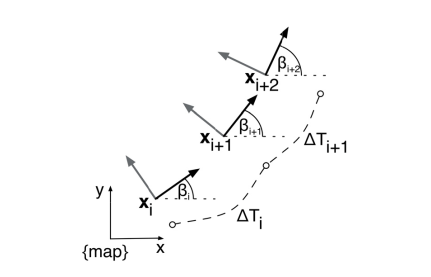
每个时差表示机器人从一个“configuration”依次过渡到下一个“configuration”所需的时间(图2)。 TEB被定义为两个序列的元组:

关键思想是通过实时优化一个加权多目标函数,在“configuration”和时间间隔方面调整和优化TEB:

其中B∗表示优化后的TEB,表示目标函数。在本文中,它是包含各个方面的分量
的加权和。 这是最基本的多目标优化方法,但已经取得了很好的效果。在未来的工作中,可能会研究更复杂的方法。
目标函数的大部分分量相对于B都是局部的,因为它们只依赖于几个连续的“configuration”,而不是整个“elastic band”。TEB的这种局部性导致了系统矩阵非常稀疏,对于这种矩阵,可以使用专门的快速有效的大规模数值优化方法【11】。
TEB的目标函数分为两类:用惩罚函数表示的速度和加速度限制等约束和与轨迹有关的目标,如路径最短、路径最快(等式18)或与障碍物的距离(等式8)。可自由使用的稀疏约束优化算法的实现在机器人框架(ROS)中不能方便的获取到。因此,在“timed elastic band”中,采用一个分段连续的、可微的代价函数来计算违反约束的惩罚(等式6)。
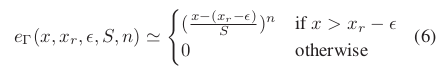
其中,为极限值,S、n和
影响近似的准确度。具体地说,S表示缩放,n表示多项式阶数,
表示近似值附近一个小位移。

图3展示了等式6不同参数时的实现。在“Approximation 1”中,S=0.1、n=2和;在“Approximation 2”中(更强的近似),S=0.05、n=2和
。上述示例显示了当约束
时的近似值。
使用多目标优化框架的一个明显优势是目标函数的模块化公式。TEB当前采用的目标函数如下所示。
2.1 Way points and obstacles
TEB在进行路标点跟踪的同时,还要避免撞到静态或动态障碍物。这两个目标函数的不同之处在于路标点吸引“elastic band”而障碍物排斥“elastic band”。目标函数取决于“timed elastic band”和路标殿或障碍物之间的最小间隔
(如图4所示)。对于路标点这种情况,距离从上界以最大目标半径
约束(等式7);在障碍物的情况下,距离从下界以最小距离
约束(等式8)。这些约束由等式6中的惩罚函数实现。

根据图3,等式8中最小间隔和最小距离约束
的符号都需要取反才能实现下界约束。
注意,这些目标函数的梯度可以解释为作用在“elastic band”上的外力。

2.2 速度和加速度
对机器人速度和加速度的动态约束通过类似于几何约束的惩罚函数来描述。图2显示了TEB的结构。根据两个连续“configurations”和
之间的欧式距离或角距离以及两个位姿之间的时间间隔
来计算平均平移速度和旋转速度。
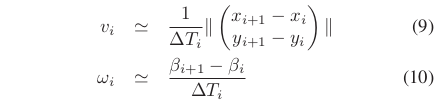
由于是邻近的“configurations”,欧式距离是两个连续位姿之间圆弧路径真实长度的充分近似。 加速度涉及到两个连续的平均速度,因此考虑具有两个相应时间间隔的三个连续“configurations”。
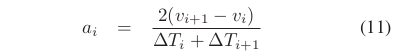
为了简洁,在等式11中三个连续的“configurations”被与它们相关的两个速度所代替。类似于等式11, 通过考虑旋转速度而非平移速度来计算的旋转加速度。考虑到移动机器人是两轮差分驱动的,可以根据以下公式计算车轮的速度与机器人中心的平移速度和旋转速度和
之间的关系:
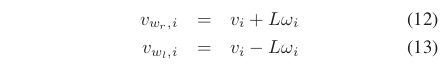
其中参数L表示机器人轴距的一半。
对等式12和等式13在时间上进行求导,可以得到相应的车轮加速度。车轮速度和加速度的上下限约束在制造商的规格中都有说明。机器人的平移惯量和转动惯量也能被包含在其中,但在第一个实现中我们还没有这样做。
2.3 Non-holonomic运动学约束

具有差分驱动的机器人仅有两个局部自由度。因此,它们只能在机器人当前方向上运动。这一运动学约束导致了机器人的平滑路径是由一系列分段圆弧组成的。因此,两个相邻的“configuration”处于具有固定曲率的同一段圆弧上,如图5所示:初始“configuration”与方向
之间的角度
必须等于最终“configuration”的对应角度
。如果令
表示机器人在第i个“configuration”的绝对方向,那么符合圆弧需要满足:

方向向量有:

相应的目标函数

惩罚值为违反该约束的二次误差。会额外考虑潜在的方向变化为180度这个情况。
2.4 最快的路径
以前的“elastic band”方法是通过收缩橡皮筋的内力来获得最短路径。由于我们的方法考虑时间信息,我们可以选择将最短路径目标更换为最快路径目标,或结合这些目标。通过最小化所有时间间隔和的平方,可以轻松实现最快路径的目标。
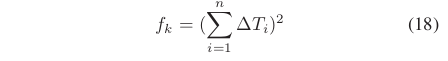
目标函数使得机器人获得最快路径,路径上的各中间“configuration”在时间上均匀分开,而非传统的空间上求最短路径。
2.5 实现
图6显示了TEB实现的控制流程。在初始化阶段,通过添加关于动力学和运动学约束的默认时间信息,将初始路径变为初始轨迹。我们的初始轨迹由分段的线性段组成,这些分段的线性段先进行纯旋转,再进行平移。这种用多边形表示的路径通常由概率路线图规划其提供【9】。另外,“Reed - shepp -paths”也可以很容易地变为到“addmissible trajectories”【10】。
在每次迭代中,算法动态地添加新的“configurations”或删除先前的“configurations”,以便将空间和时间分辨率调整到剩余的轨迹长度或规划的范围内。采用“hysteresis”来避免振荡。优化问题被转换为“hyper-graph”,并使用“ g2o”中包含的稀疏系统大规模优化算法进行求解。

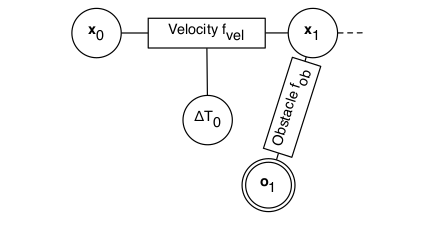
所谓的“hyper-graph”是其中一条边连接节点的数量不受限制的图。 因此,一条边可以连接两个以上的节点。TEB问题(等式4)可以转化为具有“configurations”和时间间隔作为节点的“hyper-graph”。它们与代表着给定目标函数或约束函数的边相连。图7显示了一个“hyper-graph”的示例,它有两种“configurations”,一个时差和一个点状障碍物。速度约束目标函数需要平均速度,该平均速度与两个“configurations”之间的欧氏距离和所需的行进时间有关。因此,它形成一条连接“elastic band”那些状态的边。障碍物需要一条连接到最近“configuration”的边。表示障碍物的结点是固定的(双圆),因此其参数(位置)不能由优化算法更改。
在确认能进行teb优化后(Verify trajectory),可以将计算出控制变量v和ω,直接对机器人的驱动系统进行控制。在每次新迭代之前,重新初始化阶段都会检查新的和更改中的路标殿,如果在解析“short-range”相机或激光扫描数据后接收到路标点,这将非常有用。
3 实验和结果
在这一节中,我们简要地介绍一下实验结果。
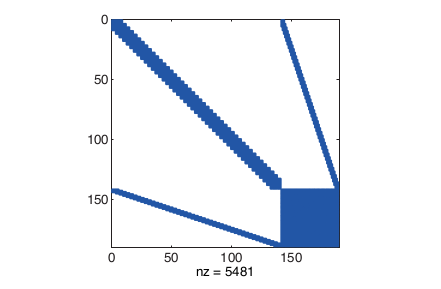
如图8所示,得到的TEB系统矩阵是一个只有15%非零元素的稀疏矩阵。在这个例子中,前141个状态对应于47个“configurations” , 而第142-189个状态与时间差
有关系。最后的这些状态与实现最快轨迹的目标函数有关,因此块比较密集,且随着TEB的尺寸呈二次增长。


图9和10显示了一个包含四个中间路标点的场景。 在第二种场景中,TEB对违反几何约束的行为采取了更强的惩罚(仿真2),因而机器人可以更准确地遍历路径点。然而,对于违反约束给予较弱的惩罚通常会使得轨迹更平滑和超调更小。可根据具体应用,调整权重使得轨迹更精确或者更平滑。考虑到动力学约束()的结果,如图11所示。图12中展示了避让静态障碍物的场景。


给“elastic band”增加时间信息和使用有效的大规模优化器求解稀疏矩阵,使得可以实时修正轨迹和控制机器人。
图13显示了用先锋2号机器人进行实验的一系列照片,其中一个人在场景中行走。先锋2号机器人由西门子 Lifebook s6410 (Core2Duo, 2.4GHz, 2GBRAM)控制,并配备了Hokuyo激光雷达,可以检测障碍物位置的动态变化。TEB通过实时调整机器人的初始轨迹(t=0),将轨迹从障碍物处拉长,避免在t∈[6,12]时间内与人发生紧急碰撞。控制周期是25ms。

4 结论和未来展望
本文提出了一种利用“time elastic band”实时修正轨迹的新方法。它在经典“elastic band”理论的基础上,增加了时间信息。该方法不仅考虑了路径上的几何约束,而且也考虑移动机器人的动力学约束。该算法能够实时运行,并直接为底层机器人运动控制器生成控制命令。该方法具有很高的灵活性,很容易适应不同的机器人运动学和应用要求。
未来的工作是开发一个稀疏约束的优化框架,现有使用惩罚函数的约束公式有点过时了。另一个不同的研究方向是使“elastic band”跳过障碍物。从技术上讲,这种方法是用一个与最近点的轨迹方向相反的“band”包围一个障碍物,在切点将它们粘合在一起,并在这一点上切割产生的轨迹,以获得从障碍物另一边通过的轨迹。优化此轨迹后,决定从障碍物的哪一侧前进。注意,这仍然是一个局部优化,不能保证找到全局最优。
5 参考文献
[1] S. M. LaValle. Planning Algorithms, Cambridge University Press, Cambridge, U.K., 2006.
[2] Quinlan, S.; Khatib, O. Elastic Bands: Connecting Path Planning and Control, IEEE Int. Conf. on Robotics and Automation (ICRA) (2), 1993
[3] Quinlan, S. Real-time modification of collision-free paths, PhD thesis, Stanford University, 1994
[4] Khatib, M. Sensor-based motion control for mobile robots, Laboratoire d’Automatique et d’Analyse des Systèmes LAAS-CNRS, 1996
[5] Khatib, M. et al. Dynamic Path Modification for Car-Like Nonholonomic Mobile Robots, IEEE Int. Conf.on Robotics and Automation (ICRA), 1997
[6] Graf, B.; Wandosell, J.M.H.; Schaeffer, C. Flexible Path Planning for Nonholonomic Mobile Robots, Fraunhofer Institute Manufacturing Engineering and Automation (IPA), 2001
[7] Brock, O.; Khatib, O. Executing Motion Plans for Robots with Many Degrees of Freedom in Dynamic Environments, IEEE Int. Conf. on Robotics and Automation (ICRA), 1998, pp. 1-6
[8] Fiorini, P.; Shiller, Z. Motion planning in dynamic environments using velocity obstacles, International Journal on Robotics Research, Vol. 17, No. 7, July 1998, pp. 760-772
[9] Kavraki, L.E. et al. Probabilistic roadmaps for path planning in high-dimensional configuration spaces, IEEE Transactions on Robotics and Automation, Vol.12, No.4, August 1996, pp.566-580
[10] Reeds, J.A.; Shepp L.A. Optimal paths for a car that goes both forwards and backwards, Pacific Journal of Mathematics, Vol. 145, No. 2, 1990, pp. 367-393
[11] Kümmerle, R. et al. g2o: A General Framework forGraph Optimization, Proc. of the IEEE Int. Conf. on Robotics and Automation (ICRA), May 2011
























 3131
3131

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








