递归（循环）神经网络(RNN)简介

原文地址http://blog.csdn.net/aws3217150

目录(?)[+]

在此之前，我们已经学习了前馈网络的两种结构——多层感知器和卷积神经网络，这两种结构有一个特点，就是假设输入是一个独立的没有上下文联系的单位，比如输入是一张图片，网络识别是狗还是猫。但是对于一些有明显的上下文特征的序列化输入，比如预测视频中下一帧的播放内容，那么很明显这样的输出必须依赖以前的输入， 也就是说网络必须拥有一定的”记忆能力”。为了赋予网络这样的记忆力，一种特殊结构的神经网络——递归神经网络(Recurrent Neural Network)便应运而生了。网上对于RNN的介绍多不胜数，这篇《Recurrent Neural Networks Tutorial》对于RNN的介绍非常直观，里面手把手地带领读者利用Python实现一个RNN语言模型，强烈推荐。为了不重复作者 Denny Britz的劳动，本篇将简要介绍RNN，并强调RNN训练的过程与多层感知器的训练差异不大(至少比CNN简单)，希望能给读者一定的信心——只要你理解了多层感知器，理解RNN便不是事儿:-)。

RNN的基本结构

首先有请读者看看我们的递归神经网络的容貌： 
 
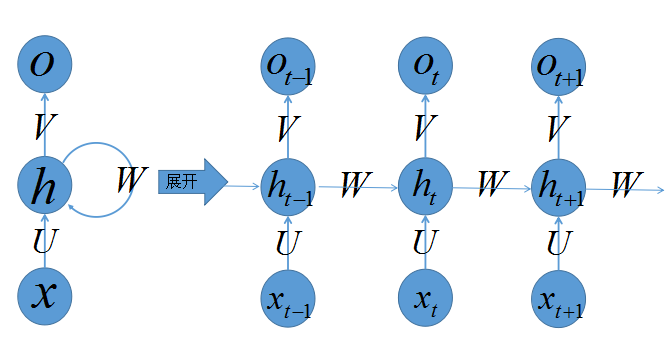
乍一看，好复杂的大家伙，没事，老样子，看我如何慢慢将其拆解，正所谓见招拆招，我们来各个击破。 
上图左侧是递归神经网络的原始结构，如果先抛弃中间那个令人生畏的闭环，那其实就是简单”输入层=>隐藏层=>输出层”的三层结构，我们在多层感知器的介绍中已经非常熟悉，然而多了一个非常陌生的闭环，也就是说输入到隐藏层之后，隐藏层还会给自己也来一发，环环相扣，晕乱复杂。 
我们知道，一旦有了环，就会陷入“先有蛋还是先有鸡”的逻辑困境，为了跳出困境我们必须人为定义一个起始点，按照一定的时间序列规定好计算顺序，做到有条不紊，于是实际上我们会将这样带环的结构展开成一个序列网络，也就是上图右侧被“unfold”之后的结构。先别急着能理解RNN，我们来点轻松的，先介绍这样的序列化网络结构包含的参数记号：

• 网络某一时刻的输入 xt ，和之前介绍的多层感知器的输入一样， xt 是一个 n 维向量，不同的是递归网络的输入将是一整个序列，也就是 x=[x0,...,xt−1,xt,xt+1,...xT] ，对于语言模型，每一个 xt 将代表一个词向量，一整个序列就代表一句话。
• ht 代表时刻 t 的隐藏状态
• ot 代表时刻 t 的输出
• 输入层到隐藏层直接的权重由 U 表示，它将我们的原始输入进行抽象作为隐藏层的输入
• 隐藏层到隐藏层的权重 W ，它是网络的记忆控制者，负责调度记忆。
• 隐藏层到输出层的权重 V ，从隐藏层学习到的表示将通过它再一次抽象，并作为最终输出。

RNN的Forward阶段

上一小节我们简单了解了网络的结构，并介绍了其中一些记号，是时候介绍它具体的运作过程了。首先在 t=0 的时刻， U,V,W 都被随机初始化好， h0 通常初始化为0，然后进行如下计算： 

s1=Ux1+Wh0h1=f(s1)o1=g(Vh1)

这样时间就向前推进，此时的状态 h1 作为时刻0的记忆状态将参与下一次的预测活动，也就是

s2=Ux2+Wh1h2=f(s2)o2=g(Vh2)

，以此类推

st=Uxt+Wht−1ht=f(Uxt+Wht−1)ot=g(Vht)

其中 f 可以是 tanh,relu,logistic 任君选择， g 通常是 softmax 也可以是其他，也是随君所欲。 
值得注意的是，我们说递归神经网络拥有记忆能力，而这种能力就是通过 W 将以往的输入状态进行总结，而作为下次输入的辅助。可以这样理解隐藏状态：

h=f(现有的输入+过去记忆总结)

RNN的Backward阶段

上一小节我们说到了RNN如何做序列化预测，也就是如何一步步预测出 o0,o1,....ot−1,ot,ot+1..... ，接下来我们来了解网络的知识 U,V,W 是如何炼成的。 
其实没有多大新意，我们还是利用在之前讲解多层感知器和卷积神经网络用到的backpropagation方法。也就是将输出层的误差 Cost ，求解各个权重的梯度 ∇U,∇V,∇W ，然后利用梯度下降法更新各个权重。现在问题就是如何求解各个权重的梯度，其它的所有东西都在之前介绍中谈到了，所有的trick都可以复用。 
由于是序列化预测，那么对于每一时刻 t ，网络的输出 ot 都会产生一定误差 et ，误差的选择任君喜欢，可以是cross entropy也可以是平方误差等等。那么总的误差为 E=∑tet ，我们的目标就是要求取

∇U=∂E∂U=∑t∂et∂U∇V=∂E∂V=∑t∂et∂V∇W=∂E∂W=∑t∂et∂W

我们知道输出 ot=g(Vst) ,对于任意的 Cost 函数，求取 ∇V 将是简单的，我们可以直接求取每个时刻的 ∂et∂V ，由于它不存在和之前的状态依赖，可以直接求导取得，然后简单地求和即可。我们重点关注 ∇W,∇U 的计算。 
回忆之前我们介绍 多层感知器的backprop算法，我们知道算法的trick是定义一个 δ=∂e∂s ，首先计算出输出层的 δL ，再向后传播到各层 δL−1,δL−2,.... ，那么如何计算 δ 呢？先看下图： 
 
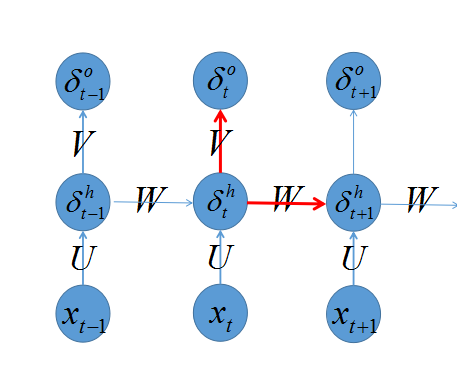
之前我们推导过，只要关注当前层次发射出去的链接即可，也就是

δht=(VTδot+WTδht+1).∗f′(st)

只要计算出所有的 δot,δht ，就可以通过以下计算出 ∇W,∇U ：

∇W=∑tδht×ht∇U=∑tδht×xt

其中 × 表示两个向量的外积。这样看来，只要你熟悉MLP的backprop算法，RNN写起程序来和MLP根本没有多大差异！手写naive的demo至少比CNN容易很多。

RNN的训练困难

虽然上一节中，我们强调了RNN的训练程序和MLP没太大差异，虽然写程序容易，但是训练起来却是千难万阻。为什么呢？因为我们的网络是根据输入而展开的，输入越长，展开的网络越深，那么对于“深度”网络训练有什么困难呢？最常见的是“gradient explode”和“gradient vanish”。这种问题在RNN中如何体现呢？为了强调这个问题，我们模仿Yoshua Bengio的论文《On the difficulty of training recurrent neural networks》的推导，重写一下RNN的梯度求解过程，为了推导方便，我们人为地为 W,U 打上标签 Wt,Ut ，即认为当确定好时间长度 T ，RNN就变成普通的MLP。打上标签后的RNN变成如下： 
 
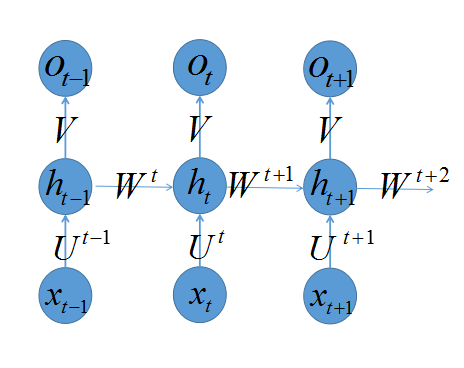
假如对于时刻 t+1 产生的误差 et+1 ，我们想计算它对于 W1,W2,....,Wt，Wt+1 的梯度，可以如下计算： 

∂et+1∂Wt+1=∂et+1∂ht+1∂ht+1∂Wt+1

∂et+1∂Wt=∂et+1∂ht+1∂ht+1∂ht∂ht∂Wt

∂et+1∂Wt−1=∂et+1∂ht+1∂ht+1∂ht∂ht∂ht−1∂ht−1∂Wt−1

......

反复运用链式法则，我们可以求出每一个 ∇W1,∇W2,....,∇Wt，∇Wt+1 ，需要注意的是，实际RNN模型对于 W,U 都是不打标签的，也就是在不同时刻都是共享同样的参数，这样可以大大减少训练参数，和CNN的共享权重类似。对于共享参数的RNN，我们只需将上述的一系列式子抹去标签并求和，就可以得到Yoshua Bengio论文中所推导的梯度计算式子： 

∂et∂W=∑1≤k≤t∂et∂ht∏k<i≤t∂hi∂hi−1∂+hk∂W

其中 ∂+hk∂W 代表不利用链式法则直接求导，也就是假如对于函数 f(h(x)) ，对其直接求导结果如下：

∂f(h(x))∂x=f′(h(x))

也就是将 h(x) 看成常数了。网上许多RNN教程都用Yoshua Bengio类似的推导，却省略了这个小步骤，使得初学者常常搞得晕头转向，摸不着头脑。论文中证明了：

||∏k<i≤t∂hi∂hi−1||≤ηt−k

从而说明了这是梯度求导的一部分环节是一个指数模型，当 η<1 时，就会出现”gradient vanish”问题，而当 η>1 时，“gradient explode”也就产生了。为了克服这样的问题，LSTM和GRU模型便后续被推出了。有趣的是，正是因为训练深度网络的困难，才导致神经网络这种古老模型沉寂了几十年，不过现在硬件的发展，训练数据的增多，神经网络重新得以复苏，并以重新以深度学习的外号杀出江湖。

参考引用

《Recurrent Neural Networks Tutorial》 
《On the difficulty of training recurrent neural networks》