【论文笔记】Filter Pruning via Geometric Median for Deep Convolutional Networks Acceleration

论文：https://arxiv.org/pdf/1811.00250.pdf
源码：https://github.com/he-y/filter-pruning-geometric-median

本篇论文来源于CVPR2019的oral，主要提出了一种基于几何中心剪枝的模型压缩方法，文章分析了基于范数阈值裁剪的局限性，提出了FPGM的裁剪方式，并经过实验验证证明了FPGM算法更加有效。

简介

在这篇论文中，指出了基于范数裁剪方式的弊端，经过试验分析作者发现基于番薯标准裁剪的效果，主要取决于两个隐含条件： 1）权重的标准差足够大 2）权重的最小的范数应该趋近于0。然而这两个条件并不能保证总是满足，为了解决这个问题文章提出了一种基于几何中心的裁剪方式，认为靠近几何中心的卷积核在划水，因此可以裁减掉这些冗余的卷积核。

contributions

1）分析了基于范数标准裁剪方式的局限性，两个条件需要被满足： 1）权重的标准差足够大 2）权重的最小的范数应该趋近于0
2）提出了几何中位数裁剪的FPGM方法，裁剪掉可替代的冗余的卷积核
3）经过试验证明FPGM真实有效

相关工作

介绍了weight pruning与filter pruning的压缩方式
weight pruning 就是细粒度的从每个卷积核里面一点一点减，具体到每个值
filter pruning 就是比较粗粒度一些，直接以卷积核为单位进行裁剪
之后又介绍了二者之前的经典算法 balabala ~~~~~

方法

分析基于范数的评价标准

Figure.2 中蓝色的是我们认为的范数分布情况，基于范数裁剪的方法在理想情况下能发挥作用，但是在真实环境下却是绿色的分布，因此说明传统的基于范数裁剪的方式具有一定的局限性。
作者预训练了一些模型，权重分布可视化效果图如下所示。

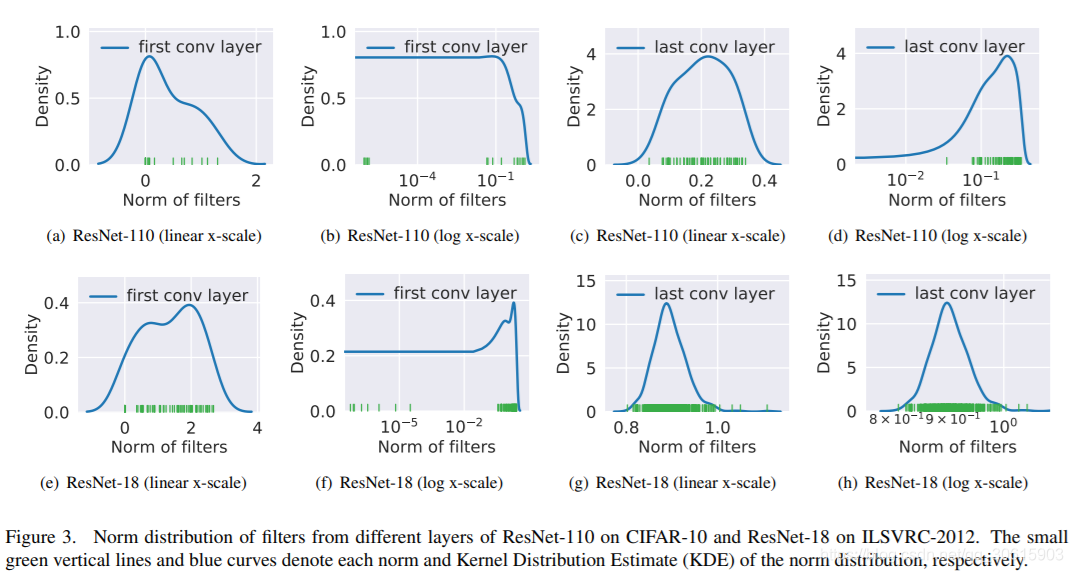
基于几何中心的评价标准FPGM

公式(1)为几何中心的计算法方式，假设在实数空间内存在n个点 $a^{(i)}$ $i\in [1,n]$ ，目标是求解在实数空间内找到到各个a点欧式距离最小的 $x$ ，$x^{\ast }$即为到各点距离和最小的几何中心

对应到本文问题上，我们当前层中的卷积核就是空间内的a点，因为用卷积核的符号替代，重新整理的后的几何中心求解公式即为公式(2) $x^{GM}$就是这些卷积核的几何中心

找到了几何中心后，顺利成章的我们就要开始找到距离几何中心最近的卷积核了，不难思考直接遍历每个卷积核，计算其与$x^{GM}$的欧式距离，然后找到最小的即可。如公式(3)所示

pesudocode

实验结果

论文中分别在Cifar-10 和 ILSVRC-2012数据集上进行实验，FPGM因为考虑到了每个滤波器之间的关系，因此取得了较好的实验结果。

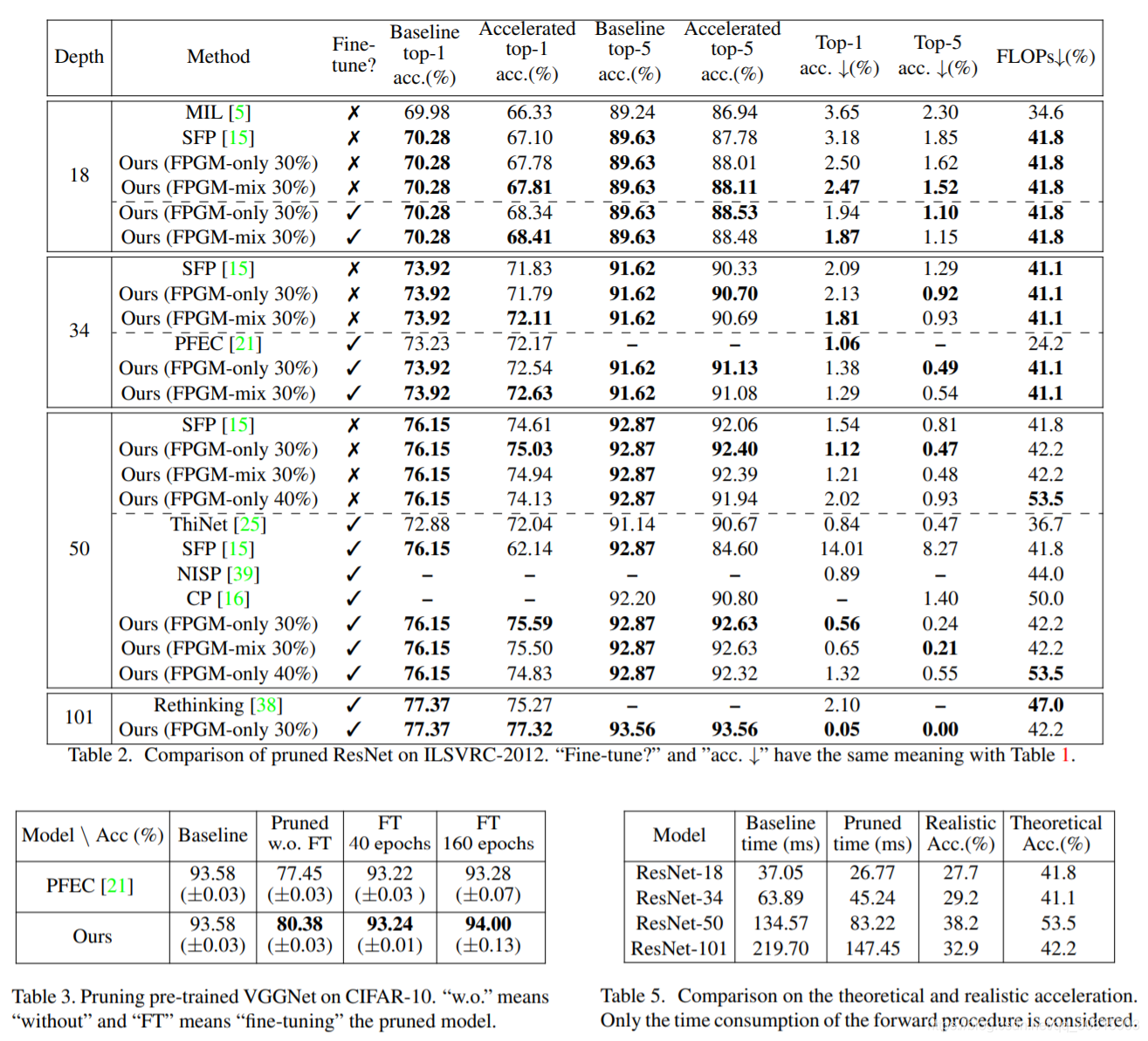
PS：（靠近几何中心的卷积核被认为是冗余的，这里存疑，划水的卷积核就应该被裁掉么？个人观点，如果卷积核彼此之间相似，那么在当前层对于该类型的featuremap就会增加，让模型更容易注意到，这是否说明对于model来说，这种类型的卷积核所关注的特征比较重要呢？）