一文读懂卡尔曼滤波——卡尔曼滤波融合IMU的陀螺仪和加速度计实践(一)

最新推荐文章于 2025-04-23 12:35:48 发布

置顶虚函数机器人

最新推荐文章于 2025-04-23 12:35:48 发布

阅读量2.2w

点赞数 39

分类专栏：传感器融合文章标签：算法卡尔曼滤波算法

本文链接：https://blog.csdn.net/qq_31775031/article/details/117067785

版权

传感器融合专栏收录该内容

3 篇文章

订阅专栏

卡尔曼的基本原理以及公式网上有很多，可以参照大神博客：

https://blog.csdn.net/m0_38089090/article/details/79523784?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162147991616780271580764%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=162147991616780271580764&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~baidu_landing_v2~default-3-79523784.pc_search_result_hbase_insert&utm_term=%E5%8D%A1%E5%B0%94%E6%9B%BCC%2B%2B&spm=1018.2226.3001.4187

卡尔曼主要在传感器上应用较多，因为传感器的噪声误差是无法避免的，如果不进行滤波等处理，噪声带来的误差只会越来越剧烈，或者导致数据根本没法使用等情况。

为了更好的理解卡尔曼，我对大神的代码稍微整理了一下并加了注释，方便阅读，但是噪声我没有用高斯噪声，这里的代码主要是对位移做了跟踪。位移到设定只是一个简单的1/2a*a哈


#include <iostream>
#include<Eigen/Core>
#include<Eigen/Dense>
#include<string>
#include<vector>
#include <cmath>
#include <limits>//用于生成随机分布数列
#include <stdlib.h>
#include <random>
using namespace std;
using namespace Eigen;
using Eigen::MatrixXd;

int main()
{
      const double dt=0.1;//采样时间
      const int MAX=500;//最大迭代次数
      double acc=0.2;//加速度 也是公式中的uk
      double theta_t;
      vector<MatrixXd> X_now;//实际位移矩阵存入这个容器中
      /*第一个公式中的变量矩阵/容器*/
      vector<MatrixXd> X_k;MatrixXd Xk=MatrixXd::Constant(2,1,0);X_k.push_back(Xk);
      vector<MatrixXd> X_k_1;MatrixXd Xk_1=MatrixXd::Constant(2,1,0);X_k_1.push_back(Xk_1);

      /*第二个公式中的变量矩阵/容器*/
      vector<MatrixXd> P_k;MatrixXd Pk=MatrixXd::Constant(2,2,0);P_k.push_back(Pk);
      vector<MatrixXd> P_k_1;MatrixXd Pk_1=MatrixXd::Constant(2,2,0);P_k_1.push_back(Pk_1);

      /*第三个公式中的变量矩阵/容器*/
      vector<MatrixXd> K_K;MatrixXd K=MatrixXd::Constant(2,2,0);K_K.push_back(K);

       /*第四个公式中的变量矩阵/容器*/
      vector<MatrixXd> Z_measure;MatrixXd Zk=MatrixXd::Constant(1,1,0);Z_measure.push_back(Zk);

      /*公式五里没有新的变量矩阵*/

      //把系数确定好
      MatrixXd A(2,2);

      MatrixXd B(2,1);
      MatrixXd H(1,2);

      A(0,0)=1;A(0,1)=dt;A(1,0)=0;A(1,1)=1;

      B(0,0)=(dt*dt)/2;B(1,0)=dt;

      H(0,0)=1;H(0,1)=0;


      //把噪声以及固定值确定好
      MatrixXd Q(2,2);//过程激励噪声协方差，假设系统的噪声向量只存在速度分量上，且速度噪声的方差是一个常量0.01，位移分量上的系统噪声为0
      Q(0,0) = 0;
      Q(1,0) = 0;
      Q(0,1) = 0;
      Q(1,1) = 0.01;

      MatrixXd R(1,1);
      R<<10;

      MatrixXd I=MatrixXd::Identity(2,2);

      //确定变量矩阵
      MatrixXd X(2,1);//实际位移值

      double noise_random;//随即噪声


      //定义时间信息tehta_t
      vector<double> time(1000, 0);
     // int i;
      for(int i = 0; i < MAX; i++)
      {
          time[i] = i * dt;
         // cout<<time[i]<<endl;
          theta_t =time[i];


         X(0,0)=1/2*acc*theta_t*theta_t  ; //实际位移，以后会用来求测量值Zk
          X(1,0)=0;
          X_now.push_back(X);
       }
      /*开始进入迭代*/
      for(int i = 1; i < MAX; i++)
      {


    /*第一个公式*/
         Xk=A*X_k_1[i-1]+B*acc;
         X_k.push_back(Xk);
     /*第二个公式*/

         Pk=A*P_k_1[i-1]*A.transpose()+Q;
         P_k.push_back(Pk);

    /*第三个公式*/
         MatrixXd tmp(1,1);
         tmp=H*P_k[i]*H.transpose()+R;
         K=P_k[i]*H.transpose()*tmp.inverse();
         K_K.push_back(K);
   /*第四个公式*/
         Zk=H*X_now[i];
         Z_measure.push_back(Zk);
         Xk_1=X_k[i]+K_K[i]*(Z_measure[i]-H*X_k[i]);
         X_k_1.push_back(Xk_1);
  /*第五个公式*/

         Pk=(I-K_K[i]*H)*P_k[i];
         P_k_1.push_back(Pk);


      }



}

OK。现在我们有了一个卡尔曼滤波的代码模板了，我们知道，只要找到参考值，再依次用代码变现五个公式，再迭代，就能得到一个效果较好的预估值了。现在我拿IMU来进行练手卡尔曼滤波。主要融合陀螺仪和加速度计两个传感器。

那么，问题来了，什么是融合？

个人理解，融合就是，用A传感器比较准确的值去校准B传感器不太准确的值来达到互补的效果。这个A，也就是你觉得比较准确到值，就是卡尔曼滤波中所谓的测量值！！！！

我们知道IMU的加速度计有误差，如果盲目积分误差会累积的非常大，但是瞬时值是准确的。陀螺仪得到的角速度也是如此，如果想得到角度，直接用角速度积分的话，角度值只会越来越漂。

卡尔曼滤波，包括一些类似最小二乘法，高斯牛顿法等等一些优化算法，本质都是为了去除掉误差对实际工程的影响。使我们得到的值无限接近于真实值，个人理解，这就是卡尔曼以及其他一些优化算法最核心的功能，而卡尔曼就是另一种形式的优化。现在我们来好好瞻仰一下这5个公式

预测的第一个公式：

把具体的数学模型转换成矩阵的形式，我们先明确我们要求啥。在IMU中，我们要求的是一个具体的横滚角的值theta。注意这个theta如果按照角速度积分的形式进行求解只会越累计越大，这时候卡尔曼就会帮助我们解决累计误差过大的问题。

OK，继续，现在我们的求解矩阵中有了一个值theta了，要不要再加一个呢？这里，我又加了一个量——bias,也就是累计误差的罪魁祸首，惯导的偏差值。bias属于IMU误差模型中的一项，很随机，但是符合高斯分布。（这里我想说一下，个人觉得随机噪声可以近似等于高斯噪声，因为完全随机的模型即为高斯模型）。好了，现在我们有了两个值了，一个是待求解的量theta，一个是我们永远无法得知的偏差值bias。变成矩阵吧： $\binom {theta}{bias}$

好了，现在我们矩阵的左端已经搞定了，现在整理一下theta和bias的公式然后得到一个完整的时序性的矩阵，我们知道，角度的估计值满足以下方程：

角度此刻估计值=上一时刻角度估计值+（当前角速度-bias）*dt

也就是： theta(k)=theta(k-1)+(angle(k)-bias)*dt

可以变成矩阵形式：

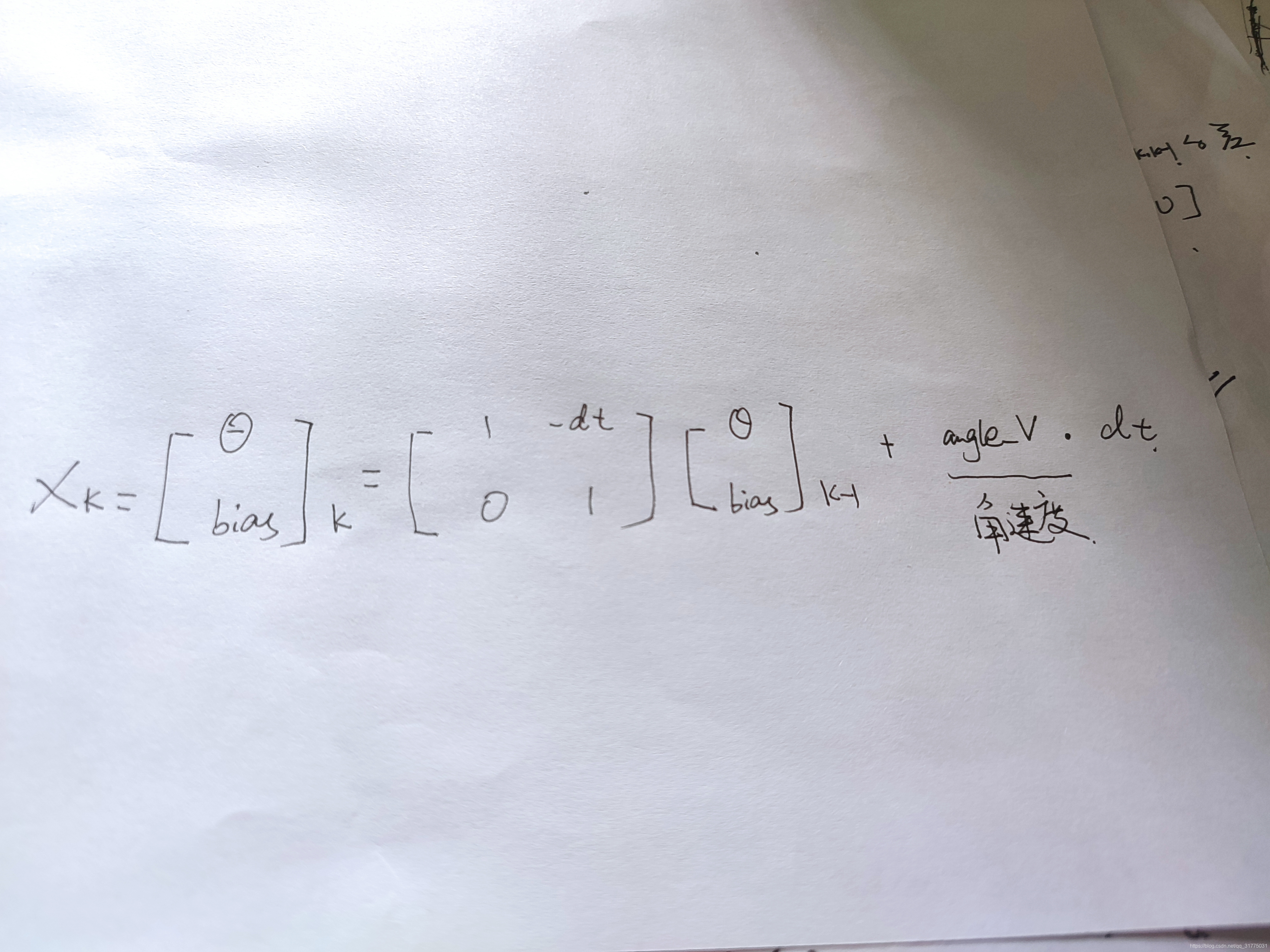
OK，现在我们有了第一个方程啦，庆祝！！！代码对应公式，如下：

 Xk_1(0,0)=(angle_V-imu.bias)*(t-1)*0.04;
 Xk_1(1,0)=imu.bias;
 X_k_1[0](0,0)=Xk_1(0,0);
 X_k_1[0](1,0)=Xk_1(1,0);

 A<<1,imu.dt*t,0,1;
 B<<imu.dt*t,0;
 Xk=A*X_k_1[t-1]+B*angle_V;
 X_k.push_back(Xk);

预测的第二个公式：

我们开始求解协防差矩阵啦！我们知道，卡尔曼滤波只有5个公式，其中两个是预测公式，预测公式的特点就是会在更新步骤中被更新，然后再反馈回去，完成迭代。协防差矩阵就是那个不幸的被更新的选手。

协防差矩阵，又名误差协防差矩阵，它在卡尔曼滤波中参与了两个操作

1. 参与了卡尔曼增益的计算

2. 和角度估计值一样，被无情的更新了。

代码中的Pk，我给了它一个初始值，因为后续它还是会被更新的，所以初始值不是太奇怪就行。

代码如下：

Pk=A*P_k_1[t-1]*A.transpose()+Qk;
P_k.push_back(Pk);

公式如下：

$P(k)=A*P(K-1)A'+Q$

问题来了，Q取多少？

个人理解，Q属于噪声，可以先设置一个数值较小的矩阵，后续再根据滤波结果来调节。但是Q越大，代表设计的卡尔曼效果越差。（噪声会不会也是一种补偿呢？）

OK，现在我们有两个公式了，继续继续！！！！！

更新的第一个公式：

这一步，我们要开始求卡尔曼增益了，公式如下：

$K=P(k)H'/(H*P(k)H'+R)$

多了个H，你是不是就糊涂加懵X了？这里的H，其实就是为了防止矩阵相乘出错的存在，比如，我们不能让2×1的矩阵和2×1的矩阵相乘，这个H就是起到了把2×1变成1×2的作用。

这个R也是个噪声。

代码如下：

MatrixXd tmp(1,1);
tmp=H*P_k[t]*H.transpose()+R;
K=P_k[t]*H.transpose()*tmp.inverse();
K_K.push_back(K);

更新的第二、三个公式

卡尔曼增益的存在，就是为了更新我们的估计值的，估计的次数多了，估计也就慢慢等于实际值（测量值）了。

公式可以参考上面的图哈，这里的Zk就是测量值了，也就是起到校准作用的值，第三个公式更新了我们的估计值，第四个公式估计了协防差，在更新协防差时多了个I矩阵，没有传感器属性的矩阵，我给它设置成了单位矩阵。

公式流程走完了，就可以开始迭代了，注意矩阵下标不要越界，就可以写好代码了。迭代指示如下：

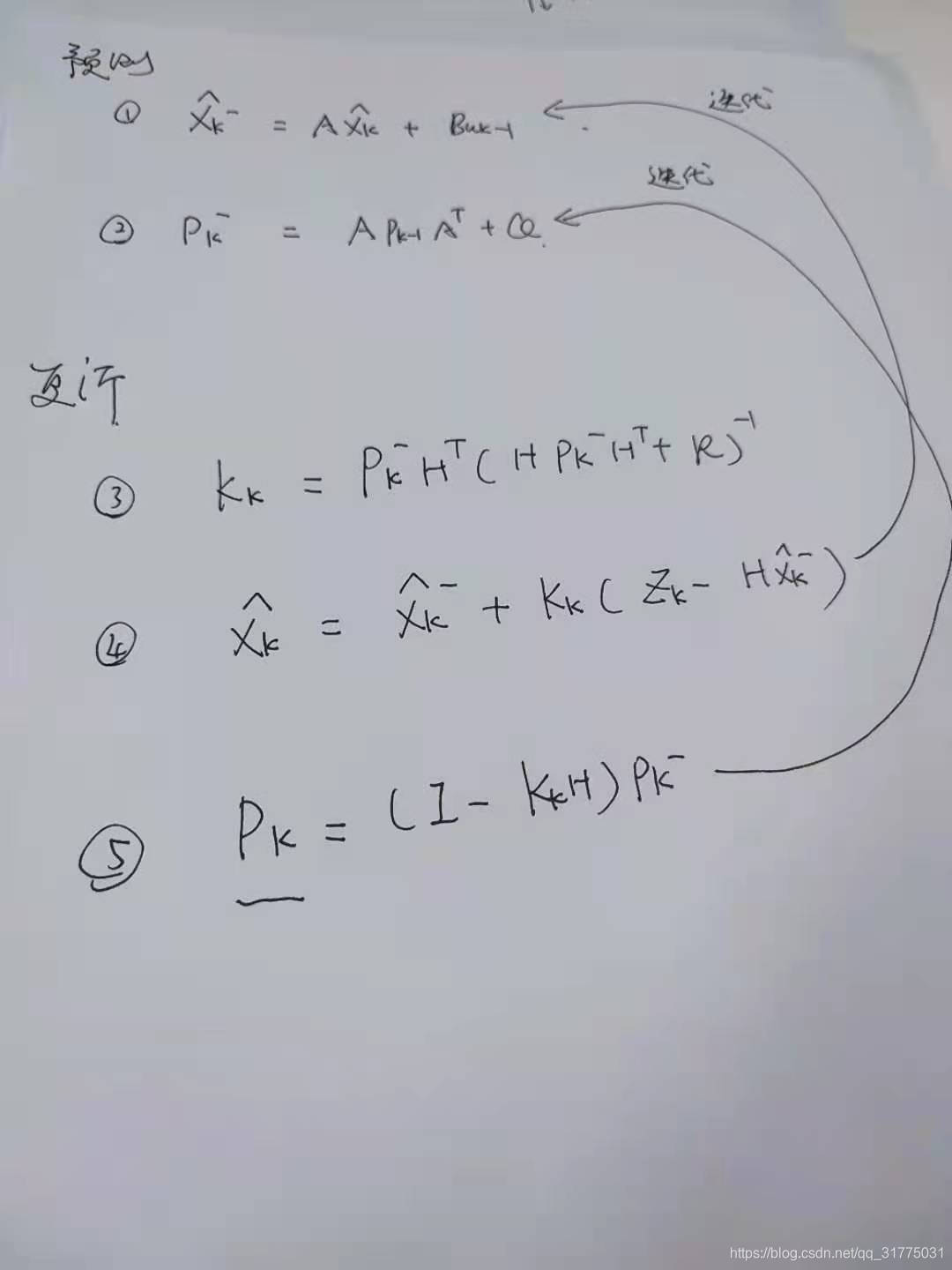
最后的卡尔曼效果如下，纵坐标=实时的估计值-实时的测量值，波动部分是人为给的随机干扰：

完整代码参考我的gitee：https://gitee.com/angry-potato/imu-kalman