Actor-Critic,演员评论家算法是强化学习中的一种很实用的方法。
比较详细的推导可以看:https://datawhalechina.github.io/easy-rl/#/chapter9/chapter9?id=actor-critic-1
文章目录
1. 简介
演员-评论家算法(Actor-Critic Algorithm) 是一种结合 policy base 和 value base 思想的算法,Actor是利用策略梯度算法实现,Critic使用时序差分实现。
- Actor(演员)是策略函数 π θ ( s ) \pi_\theta(s) πθ(s),一般用神经网络实现,输入是当前状态,输出是一个动作。该网络的训练目标是最大化累计回报的期望。
- Critic(评论家)是值函数 V π ( s ) V^\pi(s) Vπ(s),该网络可以对当前策略的值函数进行估计,也就是可以评价Actor(策略函数)的好坏。
- 原始的Actor(策略梯度法)是使用累计回报的期望作为训练依据,这样做 只有等到回合结束才能更新 π θ ( s ) \pi_\theta(s) πθ(s)的参数。
在 Actor-Critic 算法 里面,最知名的方法就是 A3C(Asynchronous Advantage Actor-Critic)。
- 如果去掉 Asynchronous,只有 Advantage Actor-Critic,就叫做 A2C。
- 如果加了 Asynchronous,变成 Asynchronous Advantage Actor-Critic,就变成 A3C。
2. Review: Policy Gradient
策略梯度法(Policy Gradient)可以参考:https://blog.csdn.net/qq_33302004/article/details/115495686
我们回顾一下policy gradient,其主要过程就是:
- 先初始化一个策略网络 θ \theta θ
- 用这个策略网络进行
N
N
N次游戏,产生
N
N
N个
τ
\tau
τ(游戏记录):
τ 1 : { s 1 1 , a 1 1 , s 2 1 , a 2 1 , . . . } , R ( τ 1 ) τ 2 : { s 1 2 , a 1 2 , s 2 2 , a 2 2 , . . . } , R ( τ 2 ) . . . τ N : { s 1 N , a 1 N , s 2 N , a 2 N , . . . } , R ( τ N ) \tau^1: \{s_1^1, a_1^1, s_2^1, a_2^1, ... \}, R(\tau^1) \\ \tau^2: \{s_1^2, a_1^2, s_2^2, a_2^2, ... \}, R(\tau^2) \\ ... \\ \tau^N: \{s_1^N, a_1^N, s_2^N, a_2^N, ... \}, R(\tau^N) \\ τ1:{s11,a11,s21,a21,...},R(τ1)τ2:{s12,a12,s22,a22,...},R(τ2)...τN:{s1N,a1N,s2N,a2N,...},R(τN) - 我们利用这
N
N
N个
τ
\tau
τ进行梯度上升,调整策略网络的参数:
∇ R ˉ ( τ ) = 1 N ∑ n = 1 N ∑ t = 1 T n ( ∑ t ′ = t T r t ′ n γ t ′ − t − b ) ∇ l o g p θ ( a t n ∣ s t n ) , γ ∈ [ 0 , 1 ] \nabla\bar{R}(\tau) = \frac1N \sum_{n=1}^N \sum_{t=1}^{T_n} (\sum_{t'=t}^T r_{t'}^n \gamma^{t'-t} - b) \nabla log p_\theta(a_t^n|s_t^n) , \gamma \in[0,1] ∇Rˉ(τ)=N1n=1∑Nt=1∑Tn(t′=t∑Trt′nγt′−t−b)∇logpθ(atn∣stn),γ∈[0,1] - 再如此重复2、3步。
3. Review: Q-Learning
Q-Learning可以参考:https://blog.csdn.net/qq_33302004/article/details/114871232
简而言之,Q-Learning就是一种 value base 的方法,该方法会建立一个Q表,里面存储了每一对 ( s , a ) (s,a) (s,a)对应的value值,agent会根据Q表中的值决定在状态 s s s下采用哪种动作。以上面的方法,agent不断与环境进行互动,并更新Q表,最终Q表不断收敛,机器人也取得了比较好的效果。
大致过程如下:
- 初始化Q表
- Repeat (for each episode):
- 初始化状态s;
- Repeat (for each step of episode):
- 依据某种策略,从Q表中根据当前状态s,选择一个动作a;
- 执行动作a,进入状态s’,获得环境反馈r;
- Q 估计 = Q ( s , a ) Q_{估计} = Q(s,a) Q估计=Q(s,a)
- Q 现实 = r + γ ∗ m a x Q ( s ′ ) Q_{现实} = r + \gamma *maxQ(s') Q现实=r+γ∗maxQ(s′),其中 r r r是在 s s s状态下执行动作 a a a的直接回报, γ \gamma γ是衰减函数, s ′ s' s′是下一个状态
- 我们利用公式更新Q表中的值:
Q
(
s
,
a
)
=
Q
估计
+
α
(
Q
现实
−
Q
估计
)
Q(s,a) = Q_{估计} + \alpha (Q_{现实} - Q_{估计} )
Q(s,a)=Q估计+α(Q现实−Q估计),其中
α
\alpha
α是学习效率,最终公式为:
Q ′ ( s , a ) = Q ( s , a ) + α ∗ [ r + γ ∗ m a x Q ( s ′ ) − Q ( s , a ) ] ; Q'(s, a) = Q(s, a) + \alpha* [r + \gamma * maxQ(s') - Q(s, a)]; Q′(s,a)=Q(s,a)+α∗[r+γ∗maxQ(s′)−Q(s,a)];
- 更新Q表,令$ Q(s, a) = Q’(s, a) $
- 更新当前状态,$ s = s’$
- until s is terminal
上面的Q-Learning是举了一个例子,其中value值的计算方法采用了时间差分(TD) 方法,在使用中还可以使用蒙特卡洛(MC) 的方法实现。

无论用TD还是MC,Q-Learning都是一种value base的方法,其核心就是计算两种函数:
- V π ( s ) V^\pi(s) Vπ(s)状态值函数,在策略 π \pi π中,状态 s s s接下来会有多少价值;
- Q π ( s , a ) Q^\pi(s,a) Qπ(s,a)动作状态值函数,在策略 π \pi π中,状态 s s s下执行动作 a a a,接下来会有多少价值;
- V π V^\pi Vπ输入 s s s,会输出一个标量;
- Q π Q^\pi Qπ输入 s s s,会输出一个向量,给每一个 a a a都分配一个value值;
- V π V^\pi Vπ和 Q π Q^\pi Qπ可以看做是两种Critic。
想要更深入理解这两种值函数,可以参考:https://blog.csdn.net/qq_33302004/article/details/115189857
4. Actor-Critic
Actor是一个policy base的方法,负责做决策,并且更新决策;Critic是一个value base的方法,负责估计当前Actor的 V π ( s ) V^\pi(s) Vπ(s)和 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a)。
Actor就是我们第二部分中提到的policy gradient,这个方法的和核心就是利用回报梯度更新网络,最终公式如下:
∇
R
ˉ
(
τ
)
=
1
N
∑
n
=
1
N
∑
t
=
1
T
n
(
∑
t
′
=
t
T
r
t
′
n
γ
t
′
−
t
−
b
)
∇
l
o
g
p
θ
(
a
t
n
∣
s
t
n
)
,
γ
∈
[
0
,
1
]
\nabla\bar{R}(\tau) = \frac1N \sum_{n=1}^N \sum_{t=1}^{T_n} (\sum_{t'=t}^T r_{t'}^n \gamma^{t'-t} - b) \nabla log p_\theta(a_t^n|s_t^n) , \gamma \in[0,1]
∇Rˉ(τ)=N1n=1∑Nt=1∑Tn(t′=t∑Trt′nγt′−t−b)∇logpθ(atn∣stn),γ∈[0,1]
其中,我们将
R
−
b
R-b
R−b这一项定义为 Advantage function(比较优势) 符号表示为
A
θ
(
s
t
,
a
t
)
A^{\theta}(s_t, a_t)
Aθ(st,at):
A
θ
(
s
t
,
a
t
)
=
∑
t
′
=
t
T
r
t
′
n
γ
t
′
−
t
−
b
A^{\theta}(s_t, a_t) = \sum_{t'=t}^T r_{t'}^n \gamma^{t'-t} - b
Aθ(st,at)=t′=t∑Trt′nγt′−t−b
我们可以看出Advantage function(比较优势) 就是利用蒙特卡洛方法计算的累计回报期望-baseline,那么我们是否可以不在Actor中计算回报,而是直接使用Critic来更新Actor呢?
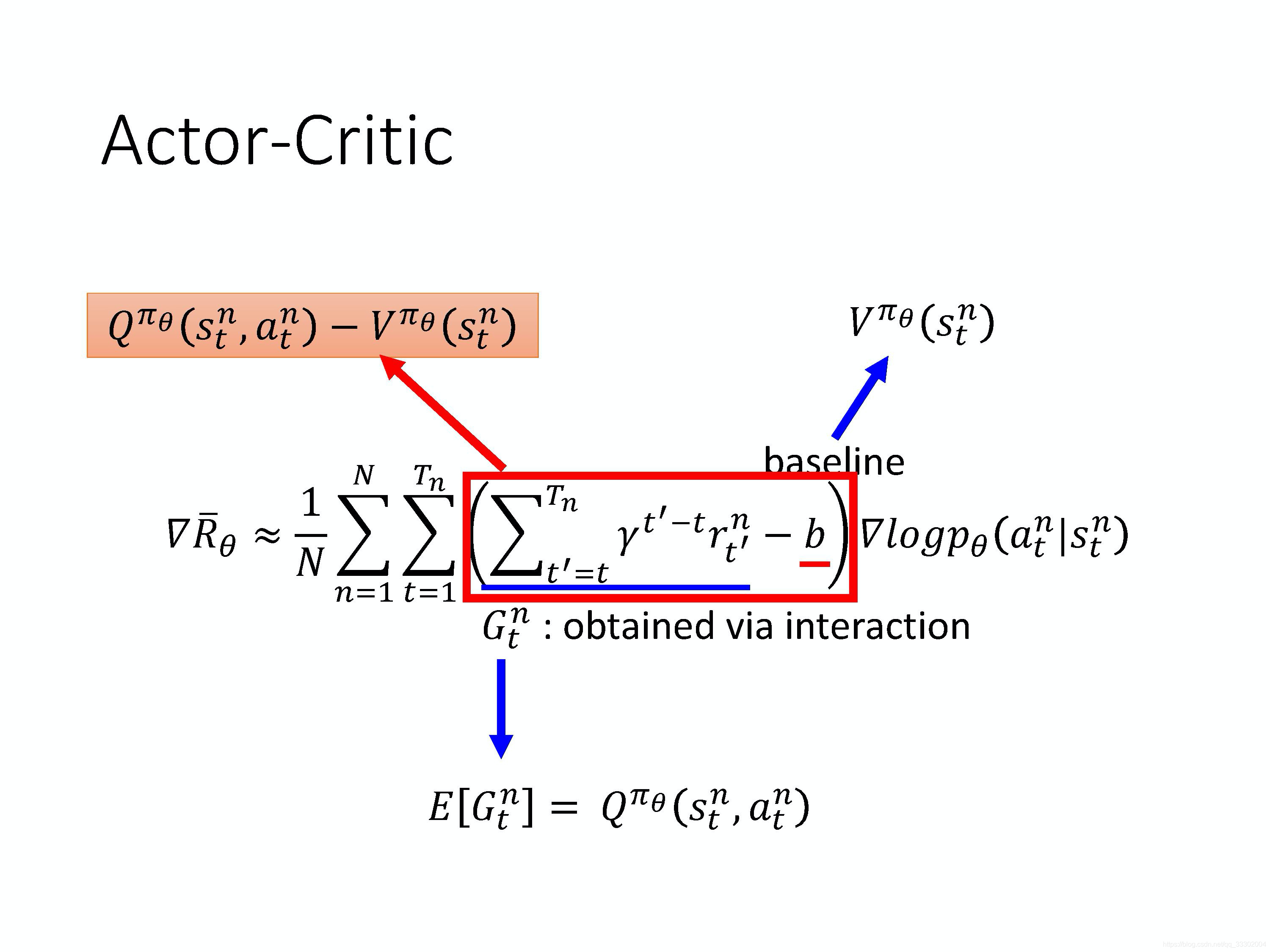
其实累计回报期望:
E
[
G
t
n
]
≈
∑
t
′
=
t
T
r
t
′
n
γ
t
′
−
t
E[G_t^n] \approx \sum_{t'=t}^T r_{t'}^n \gamma^{t'-t}
E[Gtn]≈∑t′=tTrt′nγt′−t,就是
Q
π
θ
(
s
t
n
,
a
t
n
)
Q^{\pi_\theta}(s_t^n,a_t^n)
Qπθ(stn,atn)。
因为这个就是 Q 的定义。Q-function 的定义就是在某一个状态 s,采取某一个动作 a,假设 policy 就是 π \pi π的情况下会得到的累积奖励的期望值有多大,而这个东西就是 G 的期望值。累积奖励的期望值就是 G 的期望值。
所以我们把 Q-function 套在这里就结束了,就可以把 Actor 跟 Critic 这两个方法结合起来。
对于baseline有许多不同的表示方法,但一个常见的做法是用价值函数 V π θ ( s t n ) V^{\pi_\theta}(s_t^n) Vπθ(stn) 来表示 baseline。
价值函数是说,假设 policy 是 π \pi π,在某一个状态 s 一直互动到游戏结束,期望奖励(expected reward) 有多大。 V π θ ( s t n ) V^{\pi_\theta}(s_t^n) Vπθ(stn) 是状态 s t n s_t^n stn下,执行所有 a t n a_t^n atn所产生的 Q π θ ( s t n , a t n ) Q^{\pi_\theta}(s_t^n,a_t^n) Qπθ(stn,atn)期望值,所以 Q π θ ( s t n , a t n ) − V π θ ( s t n ) Q^{\pi_\theta}(s_t^n,a_t^n) - V^{\pi_\theta}(s_t^n) Qπθ(stn,atn)−Vπθ(stn) 一定有正有负。
所以最终Actor的训练函数为:
∇
R
ˉ
(
τ
)
=
1
N
∑
n
=
1
N
∑
t
=
1
T
n
(
Q
π
θ
(
s
t
n
,
a
t
n
)
−
V
π
θ
(
s
t
n
)
)
∇
l
o
g
p
θ
(
a
t
n
∣
s
t
n
)
\nabla\bar{R}(\tau) = \frac1N \sum_{n=1}^N \sum_{t=1}^{T_n} (Q^{\pi_\theta}(s_t^n,a_t^n) - V^{\pi_\theta}(s_t^n)) \nabla log p_\theta(a_t^n|s_t^n)
∇Rˉ(τ)=N1n=1∑Nt=1∑Tn(Qπθ(stn,atn)−Vπθ(stn))∇logpθ(atn∣stn)
5. Advantage Actor-Critic
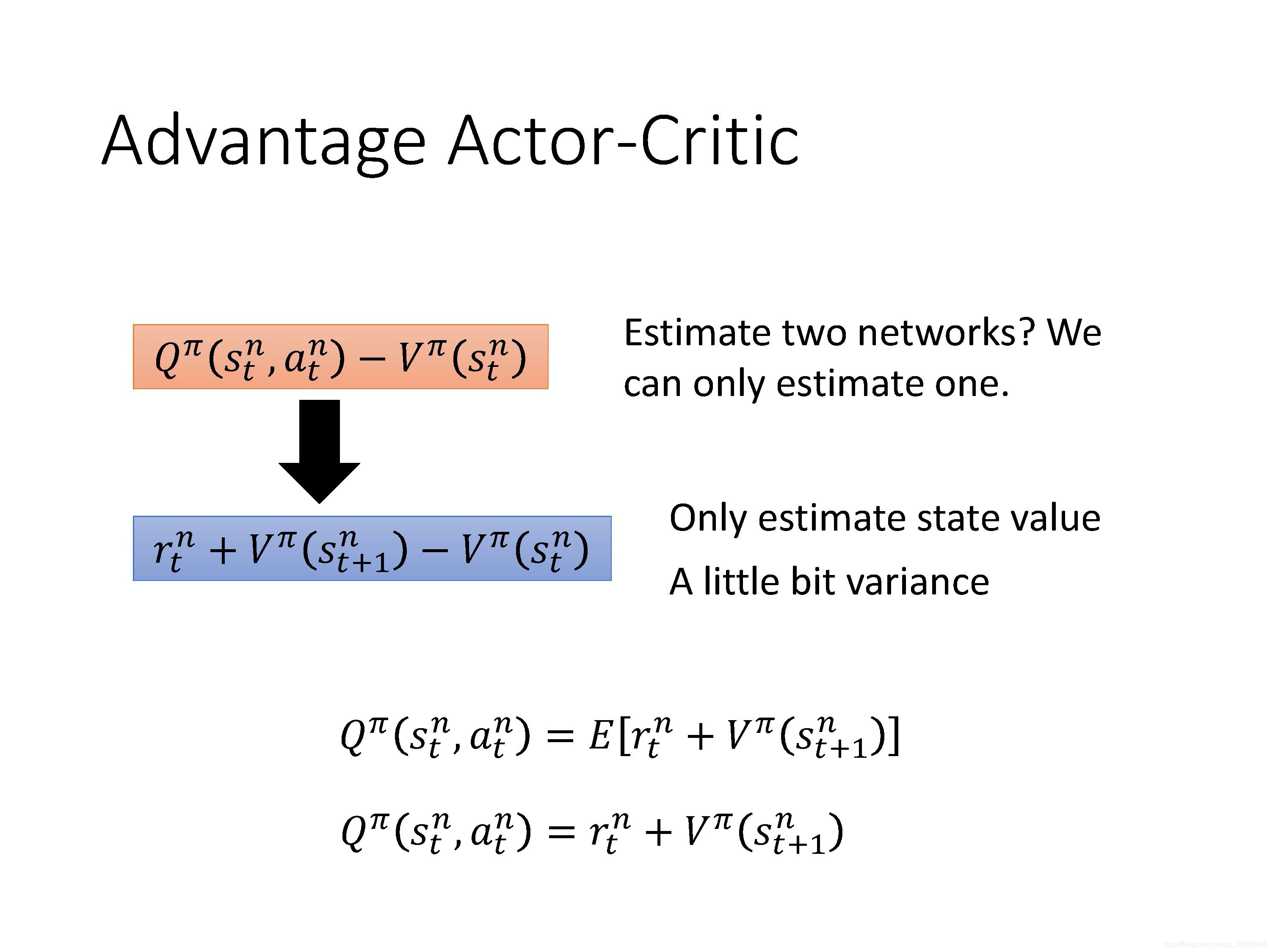
在上章中我们推导出Advantage function(比较优势) :
A
θ
(
s
t
n
,
a
t
n
)
=
Q
π
θ
(
s
t
n
,
a
t
n
)
−
V
π
θ
(
s
t
n
)
A^{\theta}(s_t^n, a_t^n) = Q^{\pi_\theta}(s_t^n,a_t^n) - V^{\pi_\theta}(s_t^n)
Aθ(stn,atn)=Qπθ(stn,atn)−Vπθ(stn)
从公式中可以看出,我们要完成两种估计,
V
π
(
s
)
V^\pi(s)
Vπ(s)和
Q
π
(
s
,
a
)
Q^\pi(s,a)
Qπ(s,a),那么直观思路就是我们需要两个网络:Q-network 和 V-network,如果这样做估测不准的风险就变成两倍。所以我们何不只估测一个网络?
事实上在这个 Actor-Critic 方法里面,我们可以只估测 V 这个网络,并且用 V 的值来表示 Q 的值,即:
Q
π
θ
(
s
t
n
,
a
t
n
)
=
E
[
r
t
n
+
V
π
θ
(
s
t
+
1
n
)
]
Q^{\pi_\theta}(s_t^n,a_t^n) = E[r_t^n+ V^{\pi_\theta}(s_{t+1}^n)]
Qπθ(stn,atn)=E[rtn+Vπθ(st+1n)]
你在状态 s s s 采取动作 a a a,会得到奖励 r r r,然后跳到状态 s t + 1 s_{t+1} st+1 。但是你会得到什么样的奖励 r r r,跳到什么样的状态 s t + 1 s_{t+1} st+1 ,它本身是有随机性的。所以要把右边这个式子,取期望值它才会等于 Q-function。
但是如果我们能够比较准确的估计
r
t
n
r_t^n
rtn就可以把期望去掉:
Q
π
θ
(
s
t
n
,
a
t
n
)
=
r
t
n
+
V
π
θ
(
s
t
+
1
n
)
Q^{\pi_\theta}(s_t^n,a_t^n) = r_t^n+ V^{\pi_\theta}(s_{t+1}^n)
Qπθ(stn,atn)=rtn+Vπθ(st+1n)
把这个期望值去掉的好处就是你不需要估计 Q 了,你只需要估计 V 就够了,你只要估计 一个网络就够了。但这样你就引入了一个随机的东西 r ,它是有随机性的,它是一个随机变量。但是这个随机变量,相较于累积奖励 G 可能还好,因为它是某一个步骤会得到的奖励,而 G 是所有未来会得到的奖励的总和。G 的方差比较大,r 虽然也有一些方差,但它的方差会比 G 要小。所以把原来方差比较大的 G 换成方差比较小的 r 也是合理的。
Q: 为什么可以直接把期望值拿掉?
A: 原始的 A3C paper 试了各种方法,最后做出来就是这个最好。当然你可能说,搞不好估计 Q 和 V,也可以估计 很好,那我告诉你就是做实验的时候,最后结果就是这个最好,所以后来大家都用这个。
由此我们的Advantage function(比较优势) 公式变成了如下的样子:
A
θ
(
s
t
n
,
a
t
n
)
=
r
t
n
+
V
π
θ
(
s
t
+
1
n
)
−
V
π
θ
(
s
t
n
)
A^{\theta}(s_t^n, a_t^n) = r_t^n+ V^{\pi_\theta}(s_{t+1}^n) - V^{\pi_\theta}(s_t^n)
Aθ(stn,atn)=rtn+Vπθ(st+1n)−Vπθ(stn)
训练梯度公式如下:
∇
R
ˉ
(
τ
)
=
1
N
∑
n
=
1
N
∑
t
=
1
T
n
(
r
t
n
+
V
π
θ
(
s
t
+
1
n
)
−
V
π
θ
(
s
t
n
)
)
∇
l
o
g
p
θ
(
a
t
n
∣
s
t
n
)
\nabla\bar{R}(\tau) = \frac1N \sum_{n=1}^N \sum_{t=1}^{T_n} (r_t^n+ V^{\pi_\theta}(s_{t+1}^n) - V^{\pi_\theta}(s_t^n)) \nabla log p_\theta(a_t^n|s_t^n)
∇Rˉ(τ)=N1n=1∑Nt=1∑Tn(rtn+Vπθ(st+1n)−Vπθ(stn))∇logpθ(atn∣stn)
因为利用了Advantage function(比较优势),所以这个方法叫做Advantage Actor-Critic,也可以叫做A2C。
整个过程如下:
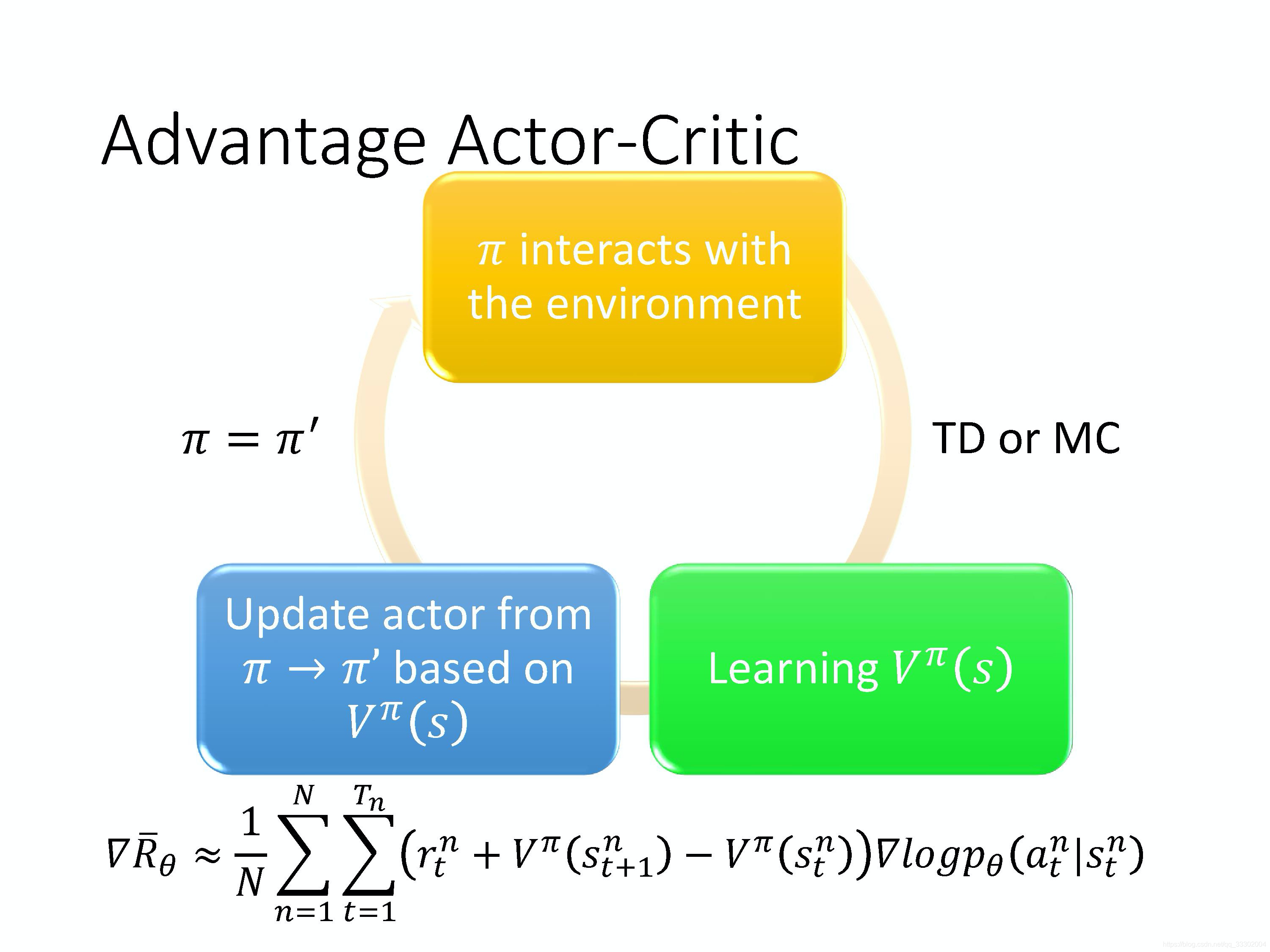
- 我们有一个Actor,他是 policy gradient 的策略网络 π \pi π,其参数用 θ \theta θ表示;
- 先利用Actor与环境互动N个回合,产生样本 τ \tau τ;
- 然后我们利用样本 τ \tau τ去训练Critic,也就是价值网络,得到 V π ( s ) V^{\pi}(s) Vπ(s),这一步可以采用TD或者MC的方法实现;
- 而后利用 V π ( s ) V^{\pi}(s) Vπ(s),我们就可以计算出 ∇ R ˉ ( τ ) \nabla\bar{R}(\tau) ∇Rˉ(τ),从而更新 π \pi π的参数,得到 θ ′ \theta' θ′;
- 更新 π \pi π,再重新与环境、产生样本、更新Critic、更新Actor,如此重复。
实现过程中的两个Tips:

实现 Actor-Critic 的时候,有两个一定会用的 tip:
- 第一个 tip 是说,我们需要估计两个网络:V function 和 policy 的网络(也就是 actor)。
- Critic 网络 V π ( s ) V^{\pi}(s) Vπ(s)输入一个状态,输出一个标量。
- Actor网络
π
(
s
)
\pi(s)
π(s)输入一个状态:
- 如果动作是离散的,输出就是一个动作的分布。
- 如果动作是连续的,输出就是一个连续的向量。
- 我们可以想到这两个网络,Actor 和 Critic 的输入都是
s
s
s,所以它们前面几个层(layer),其实是可以共享的。
- 尤其是假设你今天是玩 Atari 游戏,输入都是图像。输入的图像都非常复杂,图像很大,通常你前面都会用一些 CNN 来处理,把那些图像抽象成高级(high level)的信息。把像素级别的信息抽象成高级信息这件事情,其实对 actor 跟 critic 来说是可以共用的。所以通常你会让 actor 跟 critic 的共享前面几个层,你会让 actor 跟 critic 的前面几个层共用同一组参数,那这一组参数可能是 CNN 的参数。
- 先把输入的像素变成比较高级的信息,然后再给 actor 去决定说它要采取什么样的行为,给这个 critic,给价值函数去计算期望奖励。
- 第二个 tip 是我们一样需要探索(exploration)的机制。在做 Actor-Critic 的时候,有一个常见的探索的方法是你会对你的 \piπ 的输出的分布下一个约束。这个约束是希望这个分布的熵(entropy)不要太小,希望这个分布的熵可以大一点,也就是希望不同的动作它的被采用的概率平均一点。这样在测试的时候,它才会多尝试各种不同的动作,才会把这个环境探索的比较好,才会得到比较好的结果。
6.A3C, Asynchronous Advantage Actor-Critic
强化学习有一个问题就是它很慢,那怎么增加训练的速度呢?举个例子,火影忍者就是有一次鸣人说,他想要在一周之内打败晓,所以要加快修行的速度,他老师就教他一个方法:用影分身进行同样修行。两个一起修行的话,经验值累积的速度就会变成 2 倍,所以鸣人就开了 1000 个影分身来进行修行。这个其实就是 Asynchronous(异步的) Advantage Actor-Critic,也就是 A3C 这个方法的精神。

A3C 这个方法就是同时开很多个 worker,那每一个 worker 其实就是一个影分身。那最后这些影分身会把所有的经验,通通集合在一起。你如果没有很多个 CPU,可能也是不好实现的,你可以实现 A2C 就好。
A3C的过程如下:
- A3C 一开始有一个 global network。那我们刚才有讲过,其实 policy network 跟 value network 是绑(tie)在一起的,它们的前几个层会被绑一起。我们有一个 global network,它们有包含 policy 的部分和 value 的部分。
- 假设 global network 的参数是 θ 1 \theta_1 θ1,你会开很多个 worker。每一个 worker 就用一张 CPU 去跑。比如你就开 8 个 worker,那你至少 8 张 CPU。每一个 worker 工作前都会 global network 的参数复制过来。
- 接下来你就去跟环境做互动,每一个 actor 去跟环境做互动的时候,要收集到比较多样性的数据。举例来说,如果是走迷宫的话,可能每一个 actor 起始的位置都会不一样,这样它们才能够收集到比较多样性的数据。
- 每一个 actor 跟环境做互动,互动完之后,你就会计算出梯度。计算出梯度以后,你要拿梯度去更新你的参数。你就计算一下你的梯度,然后用你的梯度去更新 global network 的参数。就是这个 worker 算出梯度以后,就把梯度传回给中央的控制中心,然后中央的控制中心就会拿这个梯度去更新原来的参数。
- 注意,所有的 actor 都是平行跑的,每一个 actor 就是各做各的,不管彼此。所以每个人都是去要了一个参数以后,做完就把参数传回去。所以当第一个 worker 做完想要把参数传回去的时候,本来它要的参数是 θ 1 \theta_1 θ1,等它要把梯度传回去的时候。可能别人已经把原来的参数覆盖掉,变成 θ 2 \theta_2 θ2了。但是没有关系,它一样会把这个梯度就覆盖过去就是了。Asynchronous actor-critic 就是这么做的,这个就是 A3C。
7.与GAN的关系
其实 GAN 跟 Actor-Critic 的方法是非常类似的。这边就不细讲,你可以去找到一篇 paper 叫做 Connecting Generative Adversarial Network and Actor-Critic Methods。
Q: 知道 GAN 跟 Actor-Critic 非常像有什么帮助呢?
A: 一个很大的帮助就是 GAN 跟 Actor-Critic 都是以难训练而闻名的。所以在文献上就会收集各式各样的方法,告诉你说怎么样可以把 GAN 训练起来。怎么样可以把 Actor-Critic 训练起来。但是因为做 GAN 跟 Actor-Critic 的人是两群人,所以这篇 paper 里面就列出说在 GAN 上面有哪些技术是有人做过的,在 Actor-Critic 上面,有哪些技术是有人做过的。也许在 GAN 上面有试过的技术,你可以试着应用在 Actor-Critic 上,在 Actor-Critic 上面做过的技术,你可以试着应用在 GAN 上面,看看是否 work。








 本文详细介绍了Actor-Critic算法,它结合了策略梯度和值函数的思想。Actor是策略网络,Critic是值函数网络,通过策略梯度和值函数的结合来优化决策。文章回顾了Policy Gradient和Q-Learning,并讨论了Advantage Actor-Critic(A2C)和Asynchronous Advantage Actor-Critic(A3C)的区别。在A3C中,通过多线程并行学习加速训练过程。此外,还提到了Actor-Critic与GAN之间的相似性。
本文详细介绍了Actor-Critic算法,它结合了策略梯度和值函数的思想。Actor是策略网络,Critic是值函数网络,通过策略梯度和值函数的结合来优化决策。文章回顾了Policy Gradient和Q-Learning,并讨论了Advantage Actor-Critic(A2C)和Asynchronous Advantage Actor-Critic(A3C)的区别。在A3C中,通过多线程并行学习加速训练过程。此外,还提到了Actor-Critic与GAN之间的相似性。
















 4634
4634

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








