现代计算机图形学入门学习笔记-Leture04-变换续

最新推荐文章于 2024-07-10 16:21:20 发布

隋义2022

最新推荐文章于 2024-07-10 16:21:20 发布

阅读量519

点赞数

分类专栏：现代计算机图形学入门学习笔记文章标签：几何学矩阵线性代数

本文链接：https://blog.csdn.net/qq_33811591/article/details/121286261

版权

现代计算机图形学入门学习笔记专栏收录该内容

9 篇文章 1 订阅

订阅专栏

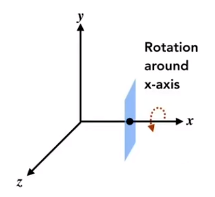
三维空间绕x、y、z轴的旋转矩阵

$R_{x}(\alpha ) = \begin{pmatrix} 1 & 0& 0& 0\\ 0& \cos \alpha & -\sin \alpha &0 \\ 0& \sin \alpha & \cos \alpha & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}$

$R_{y}(\alpha ) = \begin{pmatrix} \cos \alpha & 0& \sin \alpha& 0\\ 0& 1& 0&0 \\ -\sin \alpha& 0& \cos \alpha & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}$

$R_{z}(\alpha ) = \begin{pmatrix} \cos \alpha & -\sin \alpha& 0& 0\\ \sin \alpha& \cos \alpha& 0&0 \\ 0& 0&1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}$

y轴旋转矩阵用的是逆矩阵的原因：

旋转矩阵列元素的数值和旋转的轴向是正向对应的。

x轴由y轴叉乘z轴得到，其旋转是由y轴转向z轴, 是正向的，所以y列元素和z列元素使用的是正向旋转的值。

z轴由x轴叉乘y轴得到，其旋转是由x轴转向y轴, 是正向的，所以x列元素和y列元素使用的是正向旋转的值。

y轴由z轴叉乘x轴得到，其旋转是由z轴转向x轴, 是逆向的，正向矩阵x列元素和z列元素使用的是x轴转向z轴的值，所以要使用x轴转向z轴的负角度即z轴转向x轴，负角旋转矩阵就是其逆矩阵。

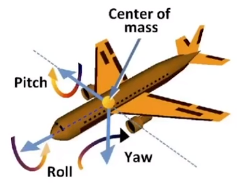
欧拉角

俯仰角(pitch)：上下俯仰

偏航角(yaw)：左右旋转

翻滚角(roll)：两侧翻滚

$R_{x,y,z}(\alpha ,\beta ,\gamma )=R_{x}(\alpha )R_{y}(\beta )R_{z}(\gamma \alpha )$

拍照的步骤

1，模型变换：摆放物体

2，视图变换：摆放相机，并且把物体转换到相机的坐标空间。

3，投影变换：把三维空间的物体投影到照片上。

视图变换

相机的定义：位置e、观察方向g、上方向t(垂直于朝向)

如何把物体转换到相机的坐标空间：

1，把相机变换到标准位置和方向：移动相机位置e到原点，旋转观察方向g到-z方向，旋转上方向t到y轴方向，旋转gxt方向到x轴方向。

2，物体做和相机相同的变换。

$M_{view} = R_{view}T_{view}$

$T_{view} = \begin{bmatrix} 1& 0& 0& -x_{e}\\ 0& 1& 0& -y_{e}\\ 0 & 0 & 1& -z_{e}\\ 0& 0& 0& 1 \end{bmatrix}$

获取旋转矩阵：

1，获取相机标准方向到当前方向的旋转矩阵，即X到g x t、Y到t、Z到-g，

2，获取步骤1旋转矩阵的逆矩阵即转置矩阵，从而得到g x t到X、t到Y、g到-Z的旋转矩阵。

$R_{X,Y,Z}(g\times t, t, -g)=\begin{bmatrix} a & b& c& 0\\ d& e& f& 0\\ g& h& i& 0\\ 0& 0& 0 & 1 \end{bmatrix}$

$\vec{x} = \begin{bmatrix} 1 & 0& 0& 0 \end{bmatrix}^{T}$

$\vec{y} = \begin{bmatrix} 0 & 1& 0& 0 \end{bmatrix}^{T}$

$\vec{z} = \begin{bmatrix} 0 & 0& 1& 0 \end{bmatrix}^{T}$

$\vec{g\times t} = \begin{bmatrix} x_{g\times t} & y_{g\times t}& z_{g\times t}& 0 \end{bmatrix}^{T}$

$\vec{t} = \begin{bmatrix} x_{t} & y_{t}& z_{t}& 0 \end{bmatrix}^{T}$

$\vec{g_{-}} = \begin{bmatrix} x_{-g} & y_{-g}& z_{-g}& 0 \end{bmatrix}^{T}$

X到g x t、Y到t、Z到-g分别进行变换：

$R_{X,Y,Z}(g\times t, t, -g)\cdot \vec{x} = \vec{g\times t}$

$R_{X,Y,Z}(g\times t, t, -g)\cdot \vec{y} = \vec{t}$

$R_{X,Y,Z}(g\times t, t, -g)\cdot \vec{z} = \vec{g_{-}}$

由此可以得出：

$R_{view}^{-1} = R_{X,Y,Z}(g\times t, t, -g) = \begin{bmatrix} x_{g\times t}& x_{t}& x_{-g}&0 \\ y_{g\times t}& y_{t}& y_{-g}&0 \\ z_{g\times t}& z_{t}& z_{-g}& 0\\ 0& 0& 0 &1 \end{bmatrix}$

$R_{view} = (R_{view}^{-1})^{-1} = (R_{view}^{-1})^{T} = \begin{bmatrix} x_{g\times t}& y_{g\times t}& z_{g\times t}& 0\\ x_{t}& y_{t}& z_{t}& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0 & 0& 0& 1 \end{bmatrix}$

变换对于任一向量和点都可成立

任一向量的变换可以拆分成X、Y、Z三个方向向量的变换：

$R_{X,Y,Z}(g\times t, t, -g)\cdot \vec{v_{xyz}} =R_{X,Y,Z}(g\times t, t, -g)\cdot (k\vec{x}+m\vec{y}+n\vec{z})= kR_{X,Y,Z}(g\times t, t, -g)\cdot \vec{x} + mR_{X,Y,Z}(g\times t, t, -g)\cdot \vec{y} + nR_{X,Y,Z}(g\times t, t, -g)\cdot \vec{z}=k\vec{g\times t}+m\vec{t}+n\vec{g_{-}}$

任一点的变换可以拆分成X、Y、Z三个方向向量和原点的变换：

$point_{0} = \begin{bmatrix} 0 & 0& 0& 1 \end{bmatrix}^{T}$

$R_{X,Y,Z}(g\times t, t, -g)\cdot point_{xyz} =R_{X,Y,Z}(g\times t, t, -g)\cdot (\vec{v_{xyz}}+point_{0}) = R_{X,Y,Z}(g\times t, t, -g)\cdot\vec{v_{xyz}} + R_{X,Y,Z}(g\times t, t, -g)\cdot point_{0} = R_{X,Y,Z}(g\times t, t, -g)\cdot\vec{v_{xyz}} + point_{0} = k\vec{g\times t}+m\vec{t}+n\vec{g_{-}} + point_{0}$

再次证明变换矩阵的正确性

投影变换

正交投影

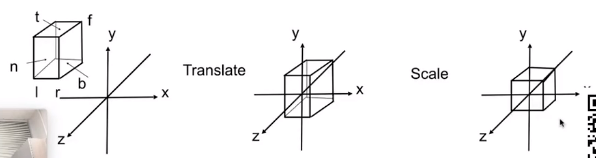
1，把场景包围盒分成六个面[l, r] x [b, t] x [f, n], 平移包围盒中心到原点。

2，把包围盒缩放成[-1, 1]的立方体。

$M_{ortho} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 &0 \\ 0& \frac{2}{t-b}& 0 &0 \\ 0& 0& \frac{2}{n-f}& 0\\ 0 & 0& 0& 1 \end{bmatrix}\begin{bmatrix} 1 & 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1 \end{bmatrix}$

透视投影

1，把视锥体压缩成立方体。

2，做正交投影。

视锥体压缩成立方体

根据相似三角形可得出任何一个点挤压后的值

$y^{'} = \frac{n}{z}y$

$x^{'} = \frac{n}{z}x$

$\begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix}\Rightarrow \begin{pmatrix} nx/z\\ ny/z\\ unknown\\ 1 \end{pmatrix}= =\begin{pmatrix} nx\\ ny\\ unknown\\ z \end{pmatrix}$

$M_{persp \to ortho} = \begin{pmatrix} n & 0& 0 &0 \\ 0 & n& 0& 0\\ ?& ?& ?&? \\ 0& 0& 1& 0 \end{pmatrix}$

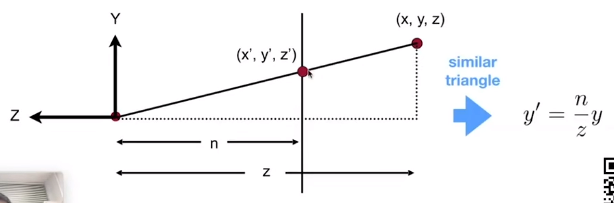
通过观察可以得到两个特点：

1，近平面上任意一点挤压后不会改变。

2，远平面上任意一点挤压后其z值不变。

代入近平面上任意一点有：

$M_{persp \to ortho}\begin{pmatrix} x\\ y\\ n\\ 1 \end{pmatrix} = \begin{pmatrix} n & 0& 0 &0 \\ 0 & n& 0& 0\\ ?& ?& ?&? \\ 0& 0& 1& 0 \end{pmatrix}\begin{pmatrix} x\\ y\\ n\\ 1 \end{pmatrix}=\begin{pmatrix} x\\ y\\ n\\ 1 \end{pmatrix}=\begin{pmatrix} nx\\ ny\\ n^{2}\\ n \end{pmatrix}$

可以得出变换矩阵的第三行为：

$\begin{pmatrix} 0 & 0& A& B \end{pmatrix}$

$\begin{pmatrix} 0 & 0& A& B \end{pmatrix}\begin{pmatrix} x\\ y\\ n\\ 1 \end{pmatrix} = n^{2}$

$An+B=n^{2}$

代入远平面上任意一点有：

$M_{persp \to ortho}\begin{pmatrix} x\\ y\\ f\\ 1 \end{pmatrix} = \begin{pmatrix} n & 0& 0 &0 \\ 0 & n& 0& 0\\ ?& ?& ?&? \\ 0& 0& 1& 0 \end{pmatrix}\begin{pmatrix} x\\ y\\ f\\ 1 \end{pmatrix}=\begin{pmatrix} nx/f\\ ny/f\\ f\\ 1 \end{pmatrix}=\begin{pmatrix} nx\\ ny\\ f^{2}\\ f \end{pmatrix}$

或者代入远平面的中心点可以快速得到：

$\begin{pmatrix} 0\\ 0\\ f\\ 1 \end{pmatrix}\Rightarrow \begin{pmatrix} 0\\ 0\\ f\\ 1 \end{pmatrix}==\begin{pmatrix} 0\\ 0\\ f^{2}\\ f \end{pmatrix}$

可以得出：

$\begin{pmatrix} 0 & 0& A& B \end{pmatrix}\begin{pmatrix} x\\ y\\ f\\ 1 \end{pmatrix} = f^{2}$

$Af+B=f^{2}$

根据

$An+B=n^{2}$

$Af+B=f^{2}$

可以得出：

$A=n+f$

$B=-nf$

$M_{persp \to ortho} = \begin{pmatrix} n & 0& 0 &0 \\ 0 & n& 0& 0\\ 0& 0& n+f&-nf \\ 0& 0& 1& 0 \end{pmatrix}$

隋义2022

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
现代计算机图形学入门学习笔记-Leture04-变换续

三维空间绕x、y、z轴的旋转矩阵y轴旋转矩阵用的是逆矩阵的原因：旋转矩阵列元素的数值和旋转的轴向是正向对应的。x轴由y轴叉乘z轴得到，其旋转是由y轴转向z轴，是正向的，所以y列元素和z列元素使用的是正向旋转的值。z轴由x轴叉乘y轴得到，其旋转是由x轴转向y轴，是正向的，所以x列元素和y列元素使用的是正向旋转的值。y轴由z轴叉乘x轴得到，其旋转是由z轴转向x轴, 是逆向的，正向矩阵x列元素和z列元素使用的是x轴转向z轴的值，所以要使用x轴转向z轴的负角度即z轴转向x轴，负角旋转
复制链接

扫一扫