非线性系统的反馈线性化

摘要 本文介绍仿射非线性系统的反馈线性化方法的基本原理和实现细节，介绍相对阶、李导数、微分同胚、最小相位、内部动态等名词解释，并举一个例子来说明线性化过程，最后展示仿真结果。
  仿射非线性或非仿射非线性指对输入是否是线性的。例如，系统能够写成 $x^{\prime }=f(x)+g(x)u$ 的形式，而不是 $x^{\prime }=f(x)+g(x)u^2$，或者 $x^{\prime }=f(x,u)$ 中提不出 $u$，如果能提出一个 $u$ 就是仿射非线性，否则就是非仿射非线性。
  本文只涉及单输入单输出的仿射非线性系统，但有多个状态。

相对阶

对系统
$$\begin{array}{rl}& {\vec{x}}^{\prime }=\vec{f}(\vec{x})+\vec{g}(\vec{x})u\\ & y=\vec{h}(\vec{x})\end{array}$$
设计 $u$ 使输出 $y$ 指数收敛。
  $y$ 的表达式中不含 $u$，将 $y$ 求导得到
$$y^{\prime }=\frac{\partial h}{\partial x}{x}^{\prime }=\frac{\partial h}{\partial x}(f+gu)=\frac{\partial h}{\partial x}f+\frac{\partial h}{\partial x}gu$$
如果 $\frac{\partial h}{\partial x}g\ne 0$，那么就能找到 $y^{\prime }$ 和 $u$ 的关系，取
$$u=\frac{1}{\frac{\partial h}{\partial x}g}(-\frac{\partial h}{\partial x}f-ky)$$
代入即可得到 $y^{\prime }=-ky$，指数收敛。
如果 $\frac{\partial h}{\partial x}g=0$，也就是 $y^{\prime }$ 中不显含 $u$，那么继续求导
$$y^{\prime \prime }=\frac{\partial (\frac{\partial h}{\partial x}f)}{\partial x}{x}^{\prime }=\frac{\partial (\frac{\partial h}{\partial x}f)}{\partial x}(f+gu)=L_f^{2}h+L_g{L}_{f}hu$$
其中
$$\begin{array}{rl}& L_{f}h=\frac{\partial h}{\partial x}f(x)\\ & L_f^{2}h=\frac{\partial (\frac{\partial h}{\partial x}f)}{\partial x}f(x)\\ & L_g{L}_{f}h=\frac{\partial (\frac{\partial h}{\partial x}f)}{\partial x}g(x)\\ & y^{\prime }=L_{f}h(x)+L_{g}h(x)u\end{array}$$
$L_g,L_f$ 称作李导数。继续下去，如果
$$L_g{L}_f^{\rho -2}h(x)=0,L_g{L}_f^{\rho -1}h(x)\ne 0$$
则称系统具有相对阶 $\rho$，此时
$$\begin{array}{rl}{y}^{(\rho )}=& L_f^{\rho }h(x)+L_g{L}_f^{\rho -1}h(x)u\\ y^{(\rho -1)}=& L_f^{\rho -1}h(x)+L_g{L}_f^{\rho -2}h(x)u=L_f^{\rho -1}h(x)\end{array}$$
也就是对 $y$ 求 $\rho$ 阶导后才能显含 $u$。$y=f(x)+g(x)u$ 的相对阶为 $0$。

微分同胚

  输出稳定不一定能得出状态稳定，因此引入可逆变换，把系统内部的所有状态分成内部动态和输出动态两部分。前面相对阶的概念是输出动态，下面引入微分同胚的概念研究内部动态。
  可逆变换 $z=T(x)$ 中，$z(t)$ 和 $x(t)$ 都可导，雅可比行列式 $\frac{\partial T(x)}{\partial x}$ 不为0。（大概率？）也就是 $x$ 和 $T(x)$ 等价，可以互换，此时称 $x$ 和 $T(x)$ 是微分同胚（diffeomorphism）的。
  取变换
$$\left[\begin{array}{c}{\xi }_1\\ {\xi }_2\\ ⋮\\ {\xi }_{\rho }\end{array}\right]=\left[\begin{array}{c}y\\ y^{\prime }\\ ⋮\\ y^{(\rho -1)}\end{array}\right]$$
这里列出了 $\rho$ 个状态，但 $x$ 有 $n$ 个状态，为了能让 $x$ 和 $z$ 微分同胚，需要对 $z$ 再补充 $n-\rho$ 个状态，记作 $\eta$，即
$$z=T(x)=\left[\begin{array}{c}\xi \\ \eta \end{array}\right]$$
其中 $\eta =\eta (x)$ 需要满足抵消条件
$$\frac{\partial \eta (x)}{\partial x}g(x)=0$$
因为当满足抵消条件时
$$\frac{\text{d}}{\text{d}t}\eta (x)=\frac{\partial \eta (x)}{\partial x}(f+gu)=\frac{\partial \eta (x)}{\partial x}f$$
可以看出 $\eta (x)$ 的导数与 $u$ 无关，完全是内部动态。除了抵消条件以外还需要满足微分同胚的条件，后面会举例说明。
（note: 可以类比前 $\rho$ 个状态客观，后 $n-\rho$ 个状态不可观）
（note: 当 $\rho =0,\rho =n,0<\rho <n$ 时分别称作可反馈线性化、不可反馈线性化、部分反馈线性化系统）
  最终变换后的标准型写作
$$\begin{array}{rl}& {\eta }^{\prime }=f_0(\eta ,\xi )\\ & {\xi }_i^{\prime }={\xi }_{i+1},1\le i\le \rho -1\\ & {\xi }_{\rho }^{\prime }=L_f^{\rho }h(x)+L_g{L}_f^{(\rho -1)}h(x)u\\ & y={\xi }_1\end{array}$$
或
$$\begin{array}{rl}& {\eta }^{\prime }=f_0(\eta ,\xi )\\ & {\xi }^{\prime }=A_c\xi +B_c\left[L_f^{\rho }h(x)+L_g{L}_f^{(\rho -1)}h(x)u\right]\\ & y=C_c\xi \end{array}$$
其中下面两式（即 ${\xi }^{\prime }$ 和 $y^{\prime }$）展开写作（以 $\rho =3$ 为例）
$$\begin{array}{rl}& \frac{\text{d}}{\text{d}t}\left[\begin{array}{c}{\xi }_1\\ {\xi }_2\\ {\xi }_3\end{array}\right]=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{\xi }_1\\ {\xi }_2\\ {\xi }_3\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\left[L_f^{\rho }h(x)+L_g{L}_f^{(\rho -1)}h(x)u\right]\\ & y=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]\left[\begin{array}{c}{\xi }_1\\ {\xi }_2\\ {\xi }_3\end{array}\right]\end{array}$$
能把仿射非线性系统转化成这种标准型就可以实现反馈线性化。

一个例子

下面举一个反馈线性化的例子，后面给出仿真证明推导过程无误。
$$\begin{array}{rl}& \left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\end{array}\right]=\left[\begin{array}{c}-x_1\\ 2x_1{x}_2\\ x_2\end{array}\right]+\left[\begin{array}{c}2{\text{e}}^{x_2}\\ 1\\ 0\end{array}\right]u\\ & y=2x_3\end{array}$$
$$\begin{array}{rl}{y}^{\prime }=& \frac{\partial h}{\partial x}f+\frac{\partial h}{\partial x}gu=L_{f}h\\ =& \left[\begin{array}{ccc}0& 0& 2\end{array}\right]\left[\begin{array}{c}-x_1\\ 2x_1{x}_2\\ x_2\end{array}\right]+\left[\begin{array}{ccc}0& 0& 2\end{array}\right]\left[\begin{array}{c}2{\text{e}}^{x_2}\\ 1\\ 0\end{array}\right]u\\ =& 2x_2\\ y^{\prime \prime }=& L_f^{2}h+L_g{L}_{f}hu\\ =& \left[\begin{array}{ccc}0& 2& 0\end{array}\right]\left[\begin{array}{c}-x_1\\ 2x_1{x}_2\\ x_2\end{array}\right]+\left[\begin{array}{ccc}0& 2& 0\end{array}\right]\left[\begin{array}{c}2{\text{e}}^{x_2}\\ 1\\ 0\end{array}\right]u\\ =& 4x_1{x}_2+2u\end{array}$$
可以看出系统相对阶为2。取 $u=-2x_1{x}_2-4y^{\prime }-4y$，则 $y^{\prime \prime }=-4y^{\prime }-4y,y(t)=(C_1+C_{2}t){\text{e}}^{-2t}$，输出稳定。
  下面设计变换查看系统内部是否稳定。定义变换
$$\begin{array}{r}T(x)=\left[\begin{array}{c}{\xi }_1\\ {\xi }_2\\ \eta \end{array}\right]=\left[\begin{array}{c}2x_3\\ 2x_2\\ \eta (x)\end{array}\right]\end{array}$$
其中 $\eta (x)$ 需要满足抵消条件
$$\begin{gathered} \frac{\partial \eta (x)}{\partial x}g(x)=0 \\ \frac{\partial \eta }{\partial x_1}2{\text{e}}^{x_2}+\frac{\partial \eta }{\partial x_2}=0 \end{gathered}$$
$\eta (x)$ 的一个解为
$$\eta (x)=x_1-2{\text{e}}^{x_2}$$
得到可逆变换 $z=T(x)$ 为
$$\begin{array}{rl}& z_1={\xi }_1=2x_3\\ & z_2={\xi }_2=2x_2\\ & z_3=\eta =x_1-2{\text{e}}^{x_2}\end{array}$$
可见雅可比矩阵 $\frac{\partial T(x)}{\partial x}$ 非奇异。此时需要注意的是如果取 $\eta (x)=x_3$ 也能满足 $(\partial \eta /\partial x)g=0$ 的条件，但此时 $\eta (x)$ 中不包含 $x_1$ 项导致雅可比矩阵的第一列全为0，不满足微分同胚的条件。
  继续化成标准型，
$${\eta }^{\prime }=x_1^{\prime }-2{\text{e}}^{x_2}{x}_2^{\prime }=(-x_1+2{\text{e}}^{x_2}u)-2{\text{e}}^{x_2}(2x_1{x}_2+u)=-x_1-4x_1{x}_2{\text{e}}^{x_2}$$
可见输入 $u$ 被抵消了。标准型中 ${\eta }^{\prime }=f_0(\eta ,\xi )$，所以接下来要把等号右边的 $x_1,x_2$ 换成 $\eta ,\xi$。将 $x_2=0.5{\xi }_2,\eta =x_1-2{\text{e}}^{x_2}$ 代入得
$$\begin{array}{rl}\eta =& x_1-2{\text{e}}^{0.5{\xi }_2},x_1=\eta +2{\text{e}}^{0.5{\xi }_2}\\ {\eta }^{\prime }=& -(\eta +2{\text{e}}^{0.5{\xi }_2})-4(\eta +2{\text{e}}^{0.5{\xi }_2})0.5{\xi }_2{\text{e}}^{0.5{\xi }_2}\\ =& -\eta -4{\xi }_2{\text{e}}^{{\xi }_2}-2(\eta {\xi }_2+1){\text{e}}^{0.5{\xi }_2}=f_0(\eta ,\xi )\end{array}$$
这样就可以写成完整的标准型形式
$$\begin{array}{rl}\eta =& -\eta -4{\xi }_2{\text{e}}^{{\xi }_2}-2(\eta {\xi }_2+1){\text{e}}^{0.5{\xi }_2}\\ \left[\begin{array}{c}{\xi }_1^{\prime }\\ {\xi }_2^{\prime }\end{array}\right]=& \left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}{\xi }_1\\ {\xi }_2\end{array}\right]+\left[\begin{array}{c}0\\ 1\end{array}\right](4x_1{x}_2+2u)\\ y=& \left[\begin{array}{cc}1& 0\end{array}\right]{\xi }_1\end{array}$$

最小相位系统

${\eta }^{\prime }=f_0(\eta ,\xi )$ 中，当 $\xi =0$ 时系统是否渐进稳定，如果是就是最小相位系统。例子中，${\eta }^{\prime }=f_0(\eta ,0)=-\eta -2$ 稳定，是最小相位系统。

仿真

系统输入设计为
$$\begin{array}{rl}u=& -2x_1{x}_2-4y^{\prime }-4y\\ =& -2x_1{x}_2-8x_2-8x_3\end{array}$$
系统结构框图如图所示。

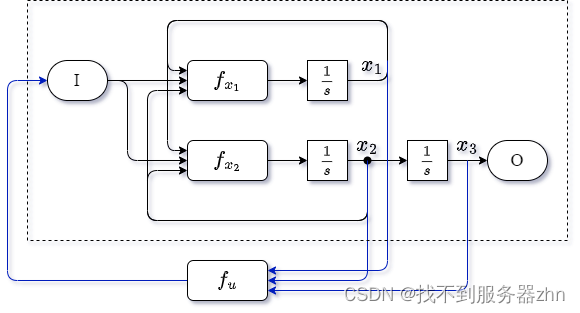
设置 $x_2(0)=1,x_1(0)=x_3(0)=0$，仿真结果如图所示。

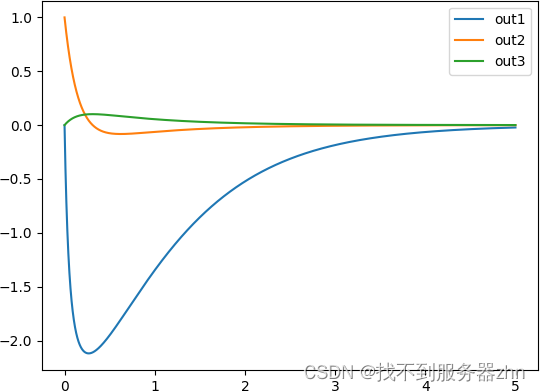
simucpp 代码如下

#include <iostream>
#include <cmath>
#include "simucpp.hpp"
using namespace simucpp;

class Plant: public PackModule {
public:
    Plant(Simulator *sim) {
        intx1 = new UIntegrator(sim, "intx1");
        intx2 = new UIntegrator(sim, "intx2");
        intx3 = new UIntegrator(sim, "intx3");
        fcnx1 = new UFcnMISO(sim, "fcnx1");
        fcnx2 = new UFcnMISO(sim, "fcnx2");
        in1 = new UGain(sim, "in1");
        sim->connectU(intx1, fcnx1);
        sim->connectU(intx2, fcnx1);
        sim->connectU(in1,   fcnx1);
        sim->connectU(intx1, fcnx2);
        sim->connectU(intx2, fcnx2);
        sim->connectU(in1,   fcnx2);
        sim->connectU(fcnx1, intx1);
        sim->connectU(fcnx2, intx2);
        sim->connectU(fcnx2, intx2);
        sim->connectU(intx2, intx3);
        intx2->Set_InitialValue(1);
        fcnx1->Set_Function([](double *u){
            double x1 = u[0], x2 = u[1], u1 = u[2];
            return 2*exp(x2)*u1 - x1;
        });
        fcnx2->Set_Function([](double *u){
            double x1 = u[0], x2 = u[1], u1 = u[2];
            return 2*x1*x2 + u1;
        });
    }
private:
    virtual PUnitModule Get_InputPort(uint n=0) const override {
        if (n==0) return in1;
        return nullptr;
    }
    virtual PUnitModule Get_OutputPort(uint n=0) const override {
        if (n==0) return intx1;
        if (n==1) return intx2;
        if (n==2) return intx3;
        return nullptr;
    }
    UIntegrator *intx1=nullptr;
    UIntegrator *intx2=nullptr;
    UIntegrator *intx3=nullptr;
    UFcnMISO *fcnx1=nullptr;
    UFcnMISO *fcnx2=nullptr;
    UGain *in1=nullptr;
};

int main() {
    Simulator sim1(5);
    auto *out1 = new UOutput(&sim1, "out1");
    auto *out2 = new UOutput(&sim1, "out2");
    auto *out3 = new UOutput(&sim1, "out3");
    auto fcnu = new UFcnMISO(&sim1, "fcnu");
    Plant *plant1 = new Plant(&sim1);
    sim1.connectU(fcnu, plant1, 0);
    sim1.connectU(plant1, 0, fcnu);
    sim1.connectU(plant1, 1, fcnu);
    sim1.connectU(plant1, 2, fcnu);
    sim1.connectU(plant1, 0, out1);
    sim1.connectU(plant1, 1, out2);
    sim1.connectU(plant1, 2, out3);
    fcnu->Set_Function([](double *u) {
        return -2*u[0]*u[1] -8*u[1] -8*u[2];
    });
    sim1.Initialize();
    sim1.Simulate();
    sim1.Plot();
    return 0;
}