03 ，二元函数，二元函数偏导数，方向导数，梯度 ：

1 ，二元函数 ： 几何意义

1. 集合意义 ：一个曲面
   
2. 定义域 ： D 为定义域
3. 值域 ： M 曲面

2 ，二元函数偏导数 ：几何意义

1. 偏导数 ： 对一个变量的导数
2. 例子 ：
   
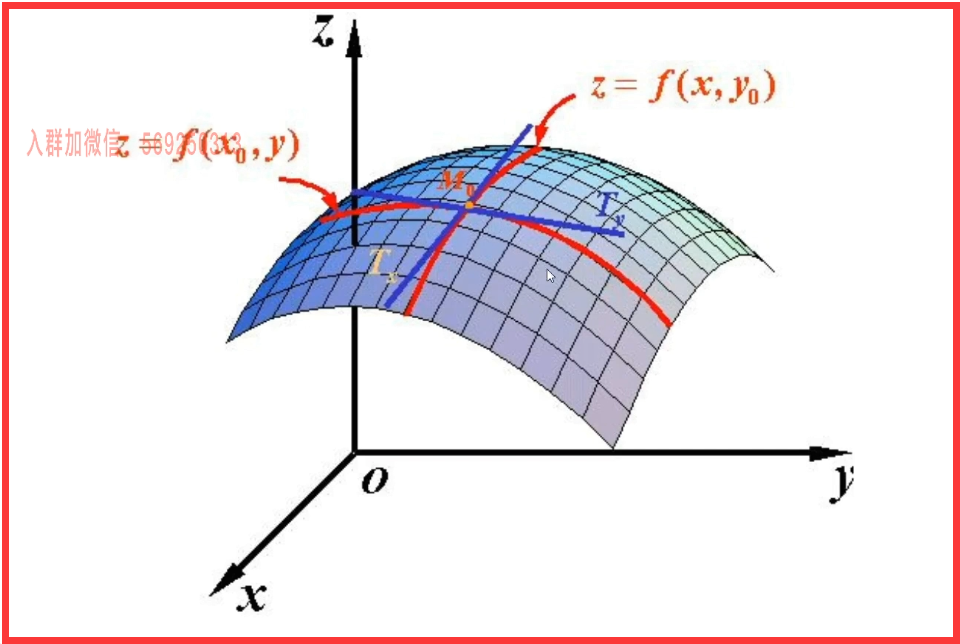
3. 理解 ：
   1 ，函数 z=f(x,y) 代表曲面
   2 ，用 y=y0 截一下，得到一条曲线
   3 ，在这条曲线上，对 x 求导，得到的依然是斜率
   4 ，本质 ： 依然是线的斜率，x 偏导数是针对 x 的斜率
   5 ，y 偏导数是针对 y 的斜率

3 ，二元函数偏导数 ： 代数运算

1. 例子 ：
   

4 ，二元函数方向导数 ： 几何理解

1. 方向导数 ： 多元函数沿任意方向的变化率
2. 如图 ：
   

5 ，二元函数方向导数 ： 代数计算

1. 例子 ： 求曲面按照 h 向量方向的
   
2. θ ： h 向量与 x 轴的夹角
3. 方向导数 ： 两个方向上的导数的三角函数加和
   
4. Du ： 方向梯度
5. 向量形式 ：
   

6 ，梯度 ： 两个偏导数形成的向量

1. 图 ：
   
2. 代数式 ：
   
3. A ： ( 点 A’ 在 x 轴方向的斜率，点 A’ 在 y 轴方向的斜率 )
4. θ ： 向量 h 与 x 轴的夹角
5. I ： ( cosθ，sinθ )
6. α ：向量 A 与向量 h 的夹角
7. 可见 ： 当向量 A 与向量 I ( 也就是向量 h ) 的夹角为 0 时，方向导数最大
8. 梯度 ：
   1 ，向量 A 叫做函数的梯度 ( 跟两个片导数有关 )
   2 ，函数在梯度的方向上变化最快
9. 变化最快 ： h 向量与 A 向量平行时，变化最快 ( 坡度最大 )