机器学习笔记之条件随机场(二)HMM vs MEMM

引言

上一节介绍了概率判别模型与概率生成模型，并简单介绍了最大熵马尔可夫模型(Maximum Entropy Markov Model,MEMM)。本节将从隐马尔可夫模型的角度介绍HMM向MEMM的演化过程。

回顾：隐马尔可夫模型

在隐马尔可夫模型——背景介绍中，已经详细介绍过隐马尔可夫模型。从动态模型(Dynamic Model)的角度观察，可以将其视作时间/序列 + 混合模型的表示形式。其泛化过程表示如下：

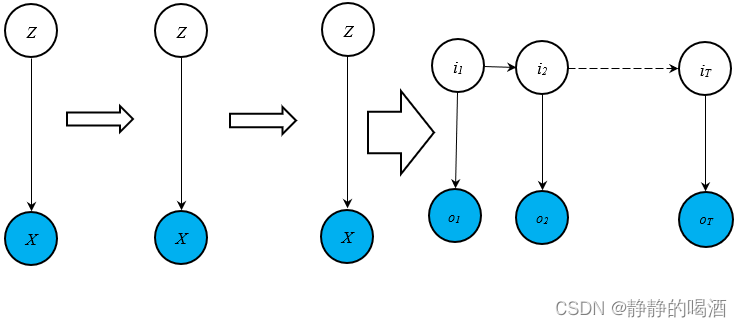
上述图像中，箭头中的每一项均可看做某时刻的混合模型。该概率图的代表性模型——高斯混合模型(Gaussian Mixture Model,GMM)

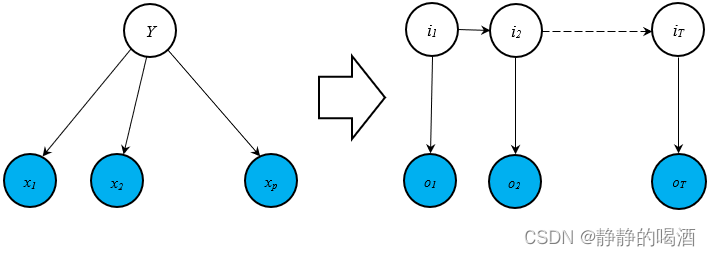
从观测变量条件独立 的角度观察，隐马尔可夫模型也可视作从隐变量 + 时间序列的角度演化形成。隐变量给定的条件下，各观测变量特征之间相互独立的代表性模型是朴素贝叶斯分类器(Naive Bayessian Classifier)。其演化过程表示如下：
上述两种泛化过程，泛化之前无论是‘高斯混合模型’，还是‘朴素贝叶斯分类器’，均没有‘动态模型’的概念。因此静态、动态概率图模型之间的共性，体现在‘隐变量’与‘观测变量’之间的关联关系中。如：‘高斯混合模型’中的$\mathcal{P}(\mathcal{Z}\mid \mathcal{X})$与‘朴素贝叶斯分类器’中$x_1,\cdots ,x_p$之间给定$\mathcal{Y}$条件下相互独立，这与隐马尔可夫模型中的‘观测独立性假设’同根同源。

隐马尔可夫模型的模型参数

隐马尔可夫模型的模型参数$\lambda =(\pi ,\mathcal{A},\mathcal{B})$分别表示为：

• $\pi$表示初始时刻的隐状态分布$\mathcal{P}(i_1)$。基于$i_1$是离散型随机变量，因而初始分布表示如下：
  概率结果需要满足：${\sum }_{k=1}^{\mathcal{K}}\mathcal{P}(i_1=q_k)=1$

  随机变量的离散取值	$q_1$	$q_2$	$\cdots$	$q_{\mathcal{K}}$
  对应概率结果	$\mathcal{P}(i_1=q_1)$	$\mathcal{P}(i_1=q_2)$	$\cdots$	$\mathcal{P}(i_1=q_{\mathcal{K}})$

• $\mathcal{A}$被称作状态转移矩阵。其表示隐状态向未来时刻转移过程的概率结果组成的矩阵：
  这里以‘一阶齐次马尔可夫’假设为例。
  $$\mathcal{A}={\left[a_{ij}\right]}_{\mathcal{K}\times \mathcal{K}}{a}_{ij}=\mathcal{P}(i_t=q_j\mid i_{t-1}=q_i)$$
• $\mathcal{B}$被称作发射矩阵(函数)。因为HMM并没有约束观测变量$o_t(t=1,2,\cdots ,T)$的类型，这里假设$o_t$同样是离散型随机变量，则发射矩阵表示如下：
  $$\mathcal{B}={\left[b_j(k)\right]}_{\mathcal{K}\times \mathcal{M}}{b}_j(k)=\mathcal{P}(o_t=v_k\mid i_t=q_j)$$

隐马尔可夫模型的两个假设

齐次马尔可夫假设仅是一种 简化运算的假设方式，针对一个基于时间/序列的隐状态的变化过程：$i_1,i_2\cdots ,i_T$，对某一时刻$t$的后验概率$\mathcal{P}(i_t\mid i_1,\cdots ,i_{t-1},i_{t+1},\cdots ,i_T)$中，真实情况下，可能每一个隐状态$i_k(k=1,2,\cdots ,T;k\ne t)$可能都与$i_t$或多或少有些关系。

• 一阶齐次马尔可夫假设：给定$t$时刻的隐变量信息$i_t$，下一时刻的隐变量结果只和当前时刻相关，与过去时刻无关：
  $$\begin{gathered} i_{t+1}\perp i_{t-1},i_{t-2},\cdots \mid i_t \\ \mathcal{P}(i_{t+1}\mid i_t,i_{t-1},\cdots ,i_1,o_t,\cdots ,o_1)=\mathcal{P}(i_{t+1}\mid i_t) \end{gathered}$$
• 同理，二阶齐次马尔可夫假设表示如下：
  $$\begin{gathered} i_{t+1}\perp i_{t-2}\mid i_t,i_{t-1} \\ \mathcal{P}(i_{t+1}\mid i_t,i_{t-1},i_{t-2},\cdots ,i_1,o_t,\cdots ,o_1)=\mathcal{P}(i_{t+1}\mid i_t,i_{t-1}) \end{gathered}$$

齐次的意思在于 不同时刻的状态转移过程，其概率分布是相同的，在隐马尔可夫模型中，这个概率分布自然是指状态转移矩阵。
通俗地说，任意时刻的状态转移过程$\mathcal{P}(i_t\mid i_{t-1})$和时刻$t$无关，它们共用同一个状态转移矩阵$\mathcal{A}$。

观测独立性假设是隐马尔可夫模型系列(隐马尔可夫模型、卡尔曼滤波、粒子滤波)的描述观测变量与隐变量之间关联关系的一种假设方式。具体表示为：某时刻观测变量$o_t$的后验概率，只和对应时刻的状态变量$i_t$相关联，与其他变量无关。
$$\mathcal{P}(o_t\mid i_t,i_{t-1},\cdots ,i_1,o_{t-1},\cdots ,o_1)=\mathcal{P}(o_t\mid i_t)$$

从贝叶斯网络的$\mathcal{D}$划分角度，同样可以观察观测变量相互独立的关系。隐马尔可夫模型局部关系表示如下：

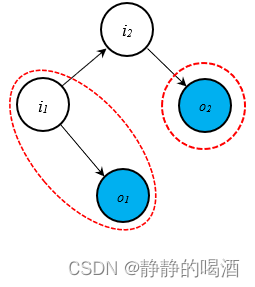
上述两个红色区域与结点$i_2$之间是顺序结构。给定$i_2$的条件下，红色区域之间的路径被阻断，$i_1,o_2$在该条件下相互独立。从而$o_1,o_2$相互独立。
各时刻观测变量之间相互独立——是‘观测独立性假设’的核心逻辑。

关于生成模型

隐马尔可夫模型本身是概率生成模型，其建模对象是针对 联合概率分布进行建模：
$$\mathcal{P}(\mathcal{O},\mathcal{I}\mid \lambda )=\mathcal{P}(o_1,\cdots ,o_T,i_1,\cdots ,i_t\mid \lambda )$$
如何去描述这个联合概率分布？示例如下：

• 示例1：当$t=1$时，联合概率分布$\mathcal{P}(\mathcal{I},\mathcal{O}\mid \lambda )$表示如下：
  $$\begin{array}{rl}\mathcal{P}(i_1,o_1\mid \lambda )& =\mathcal{P}(i_1)\cdot \mathcal{P}(o_1\mid i_1,\lambda )\\ & =\pi \cdot b_{i_1}(o_1)\end{array}$$
  其中$\pi$是初始概率分布，$b_{i_1}(o_1)$表示$i_1,o_1$对应的发射概率。

• 示例2：当$t=2$时，联合概率分布$\mathcal{P}(\mathcal{I},\mathcal{O}\mid \lambda )$表示如下：
  使用‘条件概率链式法则’进行展开。$\lambda$这里省略。它只是待学习参数，而不是结点。
  $$\mathcal{P}(i_1,i_2,o_1,o_2)=\mathcal{P}(o_2\mid o_1,i_1,i_2)\cdot \mathcal{P}(i_2\mid i_1,o_1)\cdot \mathcal{P}(o_1\mid i_1)\cdot \mathcal{P}(i_1)$$
  根据隐马尔可夫模型中结点之间的关联关系，对上式进行化简：
  贝叶斯网络的三种结构:传送门：贝叶斯网络的结构表示

  • 根据顺序结构(观测独立性假设)，有：$\mathcal{P}(o_2\mid o_1,i_1,i_2)=\mathcal{P}(o_2\mid i_2)$
  • $o_1,i_1,i_2$属于同父结构(Common Parent)，因此给定$i_1$条件下，$o_1,i_2$相互独立。因而有：$\mathcal{P}(i_2\mid i_1,o_1)=\mathcal{P}(i_2\mid i_1)$

  因而，$\mathcal{P}(i_1,i_2,o_1,o_2)$可表示为如下形式：
  $$\begin{array}{rl}\mathcal{P}(i_1,i_2,o_1,o_2)& =\mathcal{P}(o_2\mid o_1,i_1,i_2)\cdot \mathcal{P}(i_2\mid i_1,o_1)\cdot \mathcal{P}(o_1\mid i_1)\cdot \mathcal{P}(i_1)\\ & =\mathcal{P}(i_1,o_1)\cdot \mathcal{P}(i_2,o_2\mid i_1,o_1)\\ & =\mathcal{P}(i_1,o_1)\cdot \prod _{t=2}^2\mathcal{P}(i_t,o_t\mid i_{t-1},o_{t-1})\\ & =\mathcal{P}(o_2\mid i_2)\cdot \mathcal{P}(i_2\mid i_1)\cdot \mathcal{P}(o_1\mid i_1)\cdot \mathcal{P}(i_1)\\ & =\prod _{t=1}^2\mathcal{P}(i_t\mid i_{t-1})\cdot \mathcal{P}(o_t\mid i_t)\end{array}$$

以此类推，$\mathcal{P}(\mathcal{O},\mathcal{I}\mid \lambda )$可表示为：
$\lambda$记得加回去~
$$\begin{array}{rl}\mathcal{P}(\mathcal{O},\mathcal{I}\mid \lambda )& =\mathcal{P}(o_1,\cdots ,o_T,i_1,\cdots ,i_t\mid \lambda )\\ & =\mathcal{P}(i_1,o_1;\lambda )\cdot \prod _{t=2}^T\mathcal{P}(i_t,o_t\mid i_{t-1},o_{t-1};\lambda )\\ & =\prod _{t=1}^T\mathcal{P}(i_t\mid i_{t-1};\lambda )\cdot \mathcal{P}(o_t\mid i_t;\lambda )\end{array}$$

不仅在建模过程中，在模型的具体任务中同样是通过联合概率分布 进行求解。如求值问题(Evaluation)，无论是前向算法(Forward Algorithm)还是后向算法(Backward Algorithm)，都需要引入相应的隐变量，再通过对隐变量积分的形式进行求解：
$$\begin{array}{r}\mathcal{P}(\mathcal{O}\mid \lambda )=\sum _i\mathcal{P}(\mathcal{O},i\mid \lambda )\end{array}$$

MEMM VS HMM

关于隐马尔可夫模型的两个假设，思考它们的合理性。

关于这两个假设，其核心理念就是减少运算步骤，简化运算。

• 观测独立性假设：该假设使得各时刻观测变量之间相互独立。这个推论本身就不合理。

  例如：一个句子。在句子序列中的每一个单词都是一个观测值结果，从常理分析，词与词之间自然存在关联关系。但隐马尔可夫模型将这些关系忽视掉了。

• 齐次马尔可夫假设：无论是多少阶的假设，它都是约束隐变量之间关联关系的假设方式，阶数越短，条件概率越简便，越容易计算。但从关联关系的角度观察，在真实情况下，各隐变量之间可能存在复杂的关联关系。

但也可以看出：抛开简化运算不谈，从关联关系的角度，两种假设 并不是必要的。因此，尝试找到一种模型，打破隐马尔可夫模型假设的约束方式。

最大熵马尔可夫模型

最大熵马尔可夫模型的特点是 该模型打破了“观测独立性假设”。从概率图的角度观察，该模型的表述是将观测变量与隐变量之间的箭头方向置换，得到如下结果：

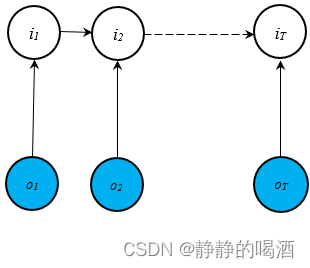
观察它的局部结构如下：

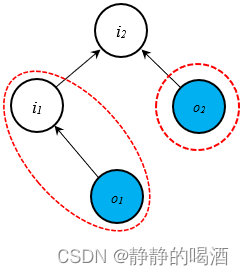
很明显，两个红色区域、结点$i_2$构成的结构是$\mathcal{V}$型结构。这意味着：在给定$i_2$的条件下，两红色区域之间存在关联关系。从而使的$o_1,o_2$之间存在关联关系。很明显。它已经打破了观测独立性假设的约束。
回顾V型结构特点:传送门

并且，最大熵马尔可夫模型是 概率判别模型，它的建模对象表示为：
$$\mathcal{P}(\mathcal{I}\mid \mathcal{O};\lambda )=\mathcal{P}(i_1,\cdots ,i_t\mid o_1,\cdots ,o_t;\lambda )$$
和生成模型相似，如何去描述这个关于隐变量的边缘概率分布？

• 示例1：当$t=2$时，对应的边缘概率$\mathcal{P}(i_1,i_2\mid o_1,o_2)$表示如下：
  这里仍然暂时忽略掉$\lambda$,依然使用‘条件概率链式法则’进行展开。
  $$\begin{array}{rl}\mathcal{P}(i_1,i_2\mid o_1,o_2)& =\mathcal{P}(i_1\mid o_1,o_2)\cdot \mathcal{P}(i_2\mid i_1,o_1,o_2)\end{array}$$
  观察$\mathcal{P}(i_1\mid o_1,o_2)$，其中$i_1$的入度只有$o_1$一个，和$o_2$之间不存在直接关联关系：
  $$\mathcal{P}(i_1\mid o_1,o_2)=\mathcal{P}(i_1\mid o_1)$$
  观察$\mathcal{P}(i_2\mid i_1,o_1,o_2)$，$i_2$的入度包含$o_1,i_2$，从而有：
  $$\mathcal{P}(i_2\mid i_1,o_1,o_2)=\mathcal{P}(i_2\mid i_1,o_2)$$
  最终有：
  $$\mathcal{P}(i_1,i_2\mid o_1,o_2)=\mathcal{P}(i_1\mid o_1)\cdot \mathcal{P}(i_2\mid i_1,o_2)$$
• 示例2(同理)：当$t=3$时，对应的边缘概率$\mathcal{P}(i_1,i_2,i_3\mid o_1,o_2,o_3)$表示如下：
  $$\begin{array}{rl}\mathcal{P}(i_1,i_2,i_3\mid o_1,o_2,o_3)& =\mathcal{P}(i_1\mid o_1,o_2,o_3)\cdot \mathcal{P}(i_2\mid i_1,o_1,o_2,o_3)\cdot \mathcal{P}(i_3\mid i_1,i_2,o_1,o_2,o_3)\\ & =\mathcal{P}(i_1\mid o_1)\cdot \mathcal{P}(i_2\mid i_1,o_2)\cdot \mathcal{P}(i_3\mid i_2,o_3)\\ & =\mathcal{P}(i_1\mid o_1)\cdot \prod _{t=2}^3\mathcal{P}(i_t\mid i_{t-1},o_t)\end{array}$$

综上，对于隐变量$\mathcal{I}$的条件概率分布$\mathcal{P}(\mathcal{I}\mid \mathcal{O};\lambda )$表示如下：
$$\begin{array}{rl}\mathcal{P}(\mathcal{I}\mid \mathcal{O};\lambda )& =\mathcal{P}(i_1,\cdots ,i_T\mid o_1,\cdots ,o_T;\lambda )\\ & =\mathcal{P}(i_1\mid o_1;\lambda )\cdot \prod _{t=2}^T\mathcal{P}(i_t\mid i_{t-1},o_t;\lambda )\end{array}$$
这是一个针对$\mathcal{P}(\mathcal{I}\mid \mathcal{O};\lambda )$标准的局部表示(针对局部表示概率图模型的表示结果)。

由于最大熵马尔可夫模型已经打破了观测独立性假设，使得各观测变量之间存在关联关系。一般地，将$\mathcal{P}(\mathcal{I}\mid \mathcal{O};\lambda )$进行全局表示：
$$\mathcal{P}(\mathcal{I}\mid \mathcal{O};\lambda )=\mathcal{P}(i_1\mid \mathcal{O};\lambda )\cdot \prod _{t=2}^T\mathcal{P}(i_t\mid i_{t-1},\mathcal{O};\lambda )$$

这种全局表示对应的概率图 描述如下：

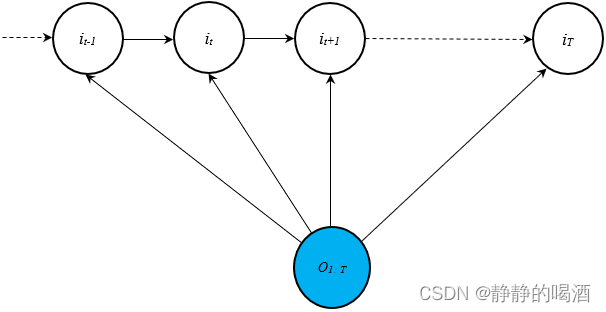
关于这种概率判别模型在状态空间模型任务 中的环境下，它比概率生成模型的优势在于：

• 任务本身就关心隐变量的后验信息(如词性标注)，相比于从联合概率分布入手的 概率生成模型，简化了运算步骤；
• 这种假设方式，打破观测独立性假设，使 观测变量的定义过程中减少了约束，使模型更加合理。

下一节将针对最大熵马尔可夫模型的缺陷，介绍条件随机场。

相关参考：
机器学习-条件随机场（2）HMM vs MEMM