本文探讨了状态空间描述和控制理论中传递函数之间的联系。通过拉氏变换，将状态空间表达式转换为传递函数阵，展示了多变量系统中输入与输出之间的耦合关系。举例说明了如何从状态空间模型求解系统的传递函数阵，强调了这种转换在系统分析中的应用。
状态空间描述和控制理论传递函数之间存在什么关系呢？
状态空间描述为一种内部描述，为了状态空间对应的输出表达，在此探讨如何从状态空间表达式导出相应的传递函数表达式。
对于最一般形式的状态空间表达式：
其中：（u应为）
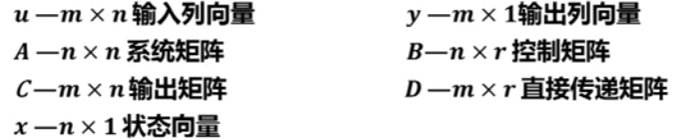
在初始条件为零的前提下，对上式作拉氏变换，得：
得到系统的传递函数阵：
其中，变换过程也非常简单，如下：
系统的传递函数是一个
的矩阵函数，设:
为G(s)的元，则系统的传递函数阵
可表示为以下的形式：
容易看出，其元都是标量函数，它在物理上表示为第j个输入对第i个输出有相互关联。称为耦合关系，这正是多变量系统的特点。
以下考虑一个实例：
对于以下系统，求系统的传递函数阵
解：由已知：
，且
（主对调，副变号）
所以，系统的传递矩阵为：
扫一扫
1524
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
