论文阅读笔记《HybridPose: 6D Object Pose Estimation under Hybrid Representations》

核心思想

  本文提出一种基于混合特征表示的位姿估计方法（HybridPose）,融合了关键点、边缘和对称点三种类型的特征，通过构建2D图像特征和3D空间特征之间的对应关系，利用EPnP算法求解目标位姿。相比于仅利用关键点特征进行位姿估计的方法而言，引入边缘和对称点特征能够提高位姿估计的稳定性。边缘特征并不是指目标物体的边缘轮廓，而是关键点之间的连线，该特征能够在图像中的关键点比较杂乱时，提高位姿估计的稳定性。而对称点特征则是描述了物体最显著的反射对称平面上对称点之间的对应关系，由于对称点数量较多，因此即使存在较大的误匹配率，仍然能够提供足够的约束。获得三种特征之后，作者先利用基于EPnP算法的位姿估计模块对位姿进行初步估计，然后利用一个鲁棒的规范化函数来筛除预测元素中的异常值，得到更准确的位姿估计结果。

实现过程

  首先，利用关键点预测网络$f_{\theta }^{\mathcal{K}}$从输入图像中预测得到$|\mathcal{K}|$个二维关键点坐标，关键点预测网络采用预训练好的PVNet算法。然后利用边缘预测网络$f_{\varphi }^{\mathcal{E}}$预测得到$|\mathcal{E}|=\frac{|\mathcal{K}|\cdot (|\mathcal{K}|-1)}{2}$个二维边缘向量，每个边缘向量是关键点构成的图的一个边。最后，利用对称点预测网络$f_{\gamma }^{\mathcal{S}}$预测$|\mathcal{S}|$组对称点的坐标，每组对称点包含两个二维点。对称点预测网络利用PVNet算法提供目标物体的分割掩码，再利用FlowNet2.0算法得到成对的对称点。由于每个三维的物体都包含很多的对称平面，对称点预测网络只输出最显著的（对称点最多的）对称平面上的对称点。
  得到三种中间特征后，就可以进行位姿估计了。已知在目标物体的标准坐标系中关键点的三维坐标为${\bar{p}}_k$，对称平面的法向量为${\bar{\mathbf{n}}}_r$，而预测网络输出的中间特征对应的齐次坐标分别为${\hat{p}}_k$，${\hat{v}}_e$，${\hat{q}}_{s,1}$和${\hat{q}}_{s,2}$（对称点中的两个点）。那么根据位姿矩阵$[R|T]$就可以构建二维图像特征和三维空间特征之间的对应关系，并得到预测结果和真实值之间的差异向量：

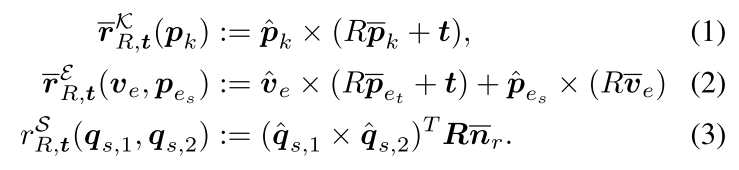
其中$e_t$和$e_s$表示边缘$e$的两个端点，${\bar{v}}_e={\bar{p}}_{e_t}-{\bar{p}}_{e_s}$。利用EPnP算法（详细介绍参看https://zhuanlan.zhihu.com/p/59070440）可以生成初始位姿。结合预测得到的三种中间特征，可以获得线性方程$$Ax=0$$其中$A$是一个矩阵，其维度为$(3|\mathcal{K}|+3|\mathcal{E}|+|\mathcal{S}|)\times 12$，$x=[r_1^T,r_2^T,r_3^T,t^T{]}_{12}^T$是包含旋转和平移参数的向量，12是旋转和平移矩阵中未知参数的维度。$A$的维度$(3|\mathcal{K}|+3|\mathcal{E}|+|\mathcal{S}|)$，我理解的是每个关键点可以提供3个约束方程（3D坐标），每个边缘可以提供3个约束方程（3D向量），每组对称点提供1个约束方程（法线向量）。为了平衡三种中间特征的重要性，给公式(2)和(3)分别赋予权重参数${\alpha }_E$和${\alpha }_S$。根据EPnP算法，可以计算$x$:

其中$v_i$表示$A$的第$i$小的右奇异向量，当$N=1$时，$x=v_1$就是最优解，然而受到预测中噪声的影响，取$N=1$的结果表现很差。因此本文与EPnP算法相同，取$N=4$。为了计算最优解$x$，需要以交替优化的方式优化中间变量${\gamma }_i$和旋转矩阵$R$，目标函数如下

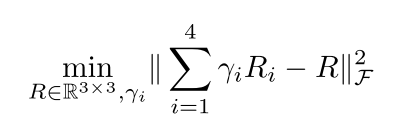
其中$R_i$是$v_i$中的前九个参数，得到最优的${\gamma }_i$后，就可以将仿射变换${\sum }_{i=1}^4{\gamma }_i{R}_i$映射为刚性变换。
  初步位姿估计仍不能够排除预测中异常点的影响，因此需要对预测结果进行优化。利用已获得目标初始位姿$R^{init},t^{init}$，可以通过局部优化的方式来获得精细化的目标位姿，引入两个差异向量来表示投影误差：

${\mathcal{P}}_{R,t}$表示利用当前位姿$(R,t)$将3D坐标点投影到2D图像坐标的过程。为了筛除掉预测结果中的异常值，本文采用German-Mcclure（GM）鲁棒函数：

通过求解以下非线性优化问题，来得到精细化的位姿估计结果：

其中${\beta }_{\mathcal{K}},{\beta }_{\mathcal{E}},{\beta }_{\mathcal{S}}$表示超参数，${\Sigma }_k$和${\Sigma }_e$分别表示关键点和边缘预测结果的协方差信息，$\Vert x{\Vert }_A=(x^{T}Ax{)}^{\frac{1}{2}}$。通过高斯-牛顿迭代法，从初始值$R^{init},t^{init}$开始优化。
本文的位姿估计的效果为

创新点

• 融合三种中间特征（关键点、边缘、对称点）对物体位姿提供更多的约束条件
• 利用EPnP算法求解初步位姿，再利用GM鲁棒函数对位姿进行优化

算法评价

  本文最大的创新在于不仅使用关键点特征对位姿进行求解，而是考虑了多种特征，提出了多种特征的提取方法，并将其有效的整合在同一个网络中。通过对EPnP算法进行改进，使其能够满足多种类型特征对应关系的位姿求解。从实验结果来看，边缘和对称点特征的引入能够有效的改善位姿估计的稳定性，但是网络的训练需要更加精细的设计。

如果大家对于深度学习与计算机视觉领域感兴趣，希望获得更多的知识分享与最新的论文解读，欢迎关注我的个人公众号“深视”。