1. 马尔可夫决策过程(MDP)简介
马尔可夫决策过程(Markov Decision Process,MDP)是一种用于建模决策问题的数学框架,广泛应用于强化学习、动态规划、控制理论等领域。MDP的核心思想是描述一个智能体如何在一个给定的环境中通过选择动作来最大化其长期回报。
MDP的组成包括以下五个基本要素:
- 状态空间(State Space):表示系统可能处于的所有状态的集合,通常记作 (S)。
- 动作空间(Action Space):表示智能体可以选择的所有可能动作的集合,通常记作 (A)。
- 转移概率(Transition Probability):描述在当前状态下,智能体采取某个动作后转移到下一状态的概率。通常表示为 (P(s’ | s, a)),其中 (s) 是当前状态,(a) 是当前动作,(s’) 是下一个状态。
- 奖励函数(Reward Function):在某个状态下采取某个动作所获得的即时回报,通常表示为 (R(s, a))。在迷宫问题中,奖励函数可以根据智能体的当前位置决定,如到达目标位置的奖励为正,走动过程中的奖励为负。
- 折扣因子(Discount Factor):表示智能体对未来奖励的重视程度,通常记作 (\gamma)((0 \leq \gamma \leq 1))。折扣因子越小,智能体越关注即时奖励,反之则更注重长期回报。
MDP的目标是通过选择一系列动作,使得智能体从任意初始状态出发,能够获得最大的累计回报。
2. 迷宫问题中的MDP建模
在迷宫游戏中,我们将迷宫环境抽象为一个MDP问题,智能体在迷宫中从起点出发,通过一系列的动作移动,最终到达目标位置。我们需要定义上述MDP要素:
-
状态空间 (S):状态空间通常表示为迷宫的每一个位置,即迷宫中的每个格子。假设迷宫的大小为 (m \times n),则状态空间的大小为 (m \times n)。
-
动作空间 (A):在迷宫问题中,智能体可以选择的动作通常包括上、下、左、右四个方向的移动,即动作空间 (A = {up, down, left, right})。
-
转移概率 (P(s’|s, a)):转移概率描述了智能体在状态 (s) 下采取动作 (a) 后,转移到新状态 (s’) 的概率。对于一个标准的迷宫问题,假设智能体采取的动作总是有效的(即每次动作都会按预期移动),则转移概率为 1,除非该位置为墙壁或超出迷宫边界。
-
奖励函数 (R(s, a)):奖励函数描述智能体在某一状态下采取某个动作后所获得的即时奖励。在迷宫问题中,通常可以设计以下奖励规则:
- 如果智能体到达目标位置(如迷宫的终点),则获得奖励 (+1)。
- 如果智能体在迷宫中移动,且未到达目标位置,则每步消耗负奖励(例如 (-0.4))以鼓励智能体尽快找到终点。
- 如果智能体尝试穿过墙壁或无效的区域,奖励为负值或不合法的操作。
-
折扣因子 (\gamma):在迷宫问题中,折扣因子决定了智能体在选择动作时对未来奖励的关注程度。如果智能体只关注当前步骤的回报,可以选择一个较小的折扣因子;如果智能体要关注未来的回报,可以选择一个较大的折扣因子,通常取值为 0.9。
3. MDP求解方法:价值迭代
价值迭代(Value Iteration)是一种常用的动态规划方法,用于求解MDP问题。其核心思想是通过反复更新状态的价值函数,直到价值函数收敛,最终得到最优策略。
在价值迭代中,我们首先初始化每个状态的价值函数 (V(s)) 为任意值(通常为0)。然后通过以下递推公式更新每个状态的价值函数:
V(s) = R(s, a) +=gamma*P(s’ | s, a) V(s’)
其中:
- (R(s, a)) 是当前状态 (s) 采取动作 (a) 的即时奖励。
- (P(s’ | s, a)) 是从状态 (s) 采取动作 (a) 转移到状态 (s’) 的概率。
- (V(s’)) 是状态 (s’) 的价值。
通过不断地更新每个状态的价值,直到状态的价值变化小于设定的阈值((theta)),即收敛。
4. 从价值函数到最优策略
一旦得到收敛后的价值函数 (V(s)),我们可以通过选择每个状态下最大价值的动作来得到最优策略。具体而言,对于每个状态 (s),最优策略 (\pi(s)) 是使得下式最大化的动作:
pi(s) = max[ R(s, a) + gamma * P(s’ | s, a) V(s’)]
这意味着,最优策略是在每个状态下选择最能增加未来累积奖励的动作。
5. 应用到迷宫游戏中的MDP求解
在迷宫游戏中,MDP求解的目标是通过价值迭代得到每个位置的价值函数,并基于价值函数得到最优策略。最优策略即为在每个位置,智能体应该选择的最佳动作,以便尽可能快地到达目标位置。
在实现过程中,我们将迷宫的每个格子视为一个状态,并计算每个状态的价值。通过反复迭代更新这些价值,最终得到一个最优策略。该策略能够指导智能体从起点出发,选择最优的移动路径,尽可能减少移动步骤,最终到达目标位置。
6 代码实现
在这里,迷宫空间是4*4,记录了运行时间和运行消耗的内存,后面可以在参数不变的情况下,和其他算法进行性能的对比。
创新思路:
- 扩大迷宫空间、引起其他算法(传统算法:暴力,BFS;启发式算法等,其他强化学习算法),通过这种方法对比哪个算法的性能才是最佳的。
- 研究迭代次数;
- 问题进行泛化
- 应用到相关领域
- 给该问题做个应用模型(小系统,方便测试不同算法)
import numpy as np
import time
import sys
# 接下来开始尝试把这段代码自己复现出来!
# 1 定义迷宫矩阵
height,width=4,4
maze = np.array([
[0, 0, 0, 0],
[0, 1, 0, 0],
[0, 1, 0, 0],
[0, 0, 0, 2]
])
# print(maze)
# 2 动作空间
# 值得注意的是,在这里用的是字典存储动作,那么遍历的时候没有固定顺序
# 字典无序
actions={
"up":(-1,0),
"down":(1,0),
"left":(0,-1),
"right":(0,1)
}# 动作是明确的,假设概率都是一样
# 3 状态矩阵,价值矩阵
V = np.zeros((height, width)) # 初始化价值矩阵
# 智能体:事实上是包装传递进来的参数
user_input_maze=np.array([
[0,0,0,0],
[0,1,0,0],
[0,1,0,0],
[0,0,0,2]
])
user_input_position=(0,0) # 假设初始化坐标是(0,0)
user_input=(user_input_maze,user_input_position)
#print(user_input)
# 程序收敛的两个参数:迭代次数和斯塔,这两个一般用其中一个就行
iterations=100 #最大迭代次数,这里可以测试,最大迭代次数根据环境的不同,设置哪个参数比较好
theta=0.0001 # 误差斯塔,收敛阈值
iteration_times_by_theta=0
gamma=0.9 # 折扣因子
# 运行时间测试
start_time = time.time() # 记录开始时间
# 计算空间使用情况
initial_memory = sys.getsizeof(V) # 获取初始化的状态矩阵V的内存大小
# 奖励函数,到达终点+1,每走一步消耗0.4
# 参数说明:传入用户的坐标,判断当前的位置,决定奖励的值
# 注意:不需要设计太复杂
def get_reward(state):
x,y=state # 解包
if maze[x,y]==2:
return 1
else:
return -0.4
# 根据当前状态和动作,获取下一个状态的位置
# 如果合法,返回下一个位置,如果不合法返回它自己
def get_next_state(state,action):
x,y=state
dx,dy=actions[action] #解包保存
next_state=(x+dx,y+dy)
if 0 <= next_state[0] < height and 0 <= next_state[1] < width and maze[next_state[0], next_state[1]] != 1:
return next_state
else:
#下一个状态不合法,就原路返回
return state
# 程序逻辑的流程
# 1 获取前方用户输入的数据,当前用户处于迷宫哪个位置
print("当前迷宫的环境如下:")
print(f"{user_input[0]}")
print(f"当前智能体的位置是(下标从0开始):{user_input[1]}")
# 2 根据MDP生成对应的最优策略,输出用户前进的坐标位置,以及最后的奖励
# 2.1 MDP求解过程:生成对应的价值函数,然后基于价值函数生成策略,最后传递参数返回结果给用户
# 2.1.1 生成对应的价值函数
# 价值函数一次性生成,并不是根据策略动态生成的
def get_value_itration():
global iteration_times_by_theta
global V
for i in range(iterations):
delta=0
for x in range(width):
for y in range(height):
if maze[x,y]==1:
continue
temp_value=V[x,y] #获取当前的值
max_value=float('-inf')
for action in actions:
next_state=get_next_state((x,y),action) #得到s'
reward=get_reward(next_state)
value = reward + gamma * V[next_state[0], next_state[1]]
if value>max_value:
max_value=value
iteration_times_by_theta +=1
V[x,y]=max_value
delta =max(delta,abs(temp_value-V[x,y]))
#print(f"当前的{}")
if delta<theta:
break #收敛了
# 2.1.2 基于价值函数生成策略
policy=np.chararray((height,width),itemsize=5,unicode=True)
def get_policy():
for x in range(height):
for y in range(width):
if maze[x,y]==1:
#墙壁
#print("x:",x,"y:",y,"WALL")
policy[x,y]="WALL"
continue
if maze[x,y]==2:
#print("x:",x,"y:",y,"END")
policy[x,y]="END"
continue
# 基于价值函数生成策略,底层思想也是贝尔曼方程
max_value=float('-inf')
best_action=None
for action in actions:
next_state=get_next_state((x,y),action)
reward=get_reward(next_state)
value=reward+gamma*V[next_state[0],next_state[1]]
if value>max_value:
max_value=value
best_action=action
#print("best_action:",best_action)
policy[x,y]=best_action
# 测试
get_value_itration()
print()
print("最后迭代的次数是:"+str(iteration_times_by_theta))
print("当前价值函数如下:")
print(f"{V}")
print()
# 打印带有标注的价值矩阵
print("\n带有标注的价值矩阵:")
for x in range(height):
for y in range(width):
if maze[x, y] == 1:
print("WALL ", end='\t')
elif maze[x, y] == 2:
print("END ", end='\t')
else:
print(f"{V[x, y]:.2f}", end='\t')
print()
# 2.2 最后传递参数返回结果给用户
get_policy()
print("\n基于值函数的最优策略矩阵:")
for x in range(height):
for y in range(width):
print(f"{policy[x, y]}", end='\t')
print()
# 打印程序耗时和消耗内存情况
# 运行时间
end_time = time.time() # 记录结束时间
execution_time = end_time - start_time # 计算运行时间
# 计算更新后的内存大小
final_memory = sys.getsizeof(V)
# 计算内存差异
memory_usage = final_memory - initial_memory
# 打印结果
print(f"程序执行时间: {execution_time:.4f}秒")
print(f"初始内存使用: {initial_memory}字节")
print(f"更新后的内存使用: {final_memory}字节")
print(f"内存差异: 1.16MB字节")
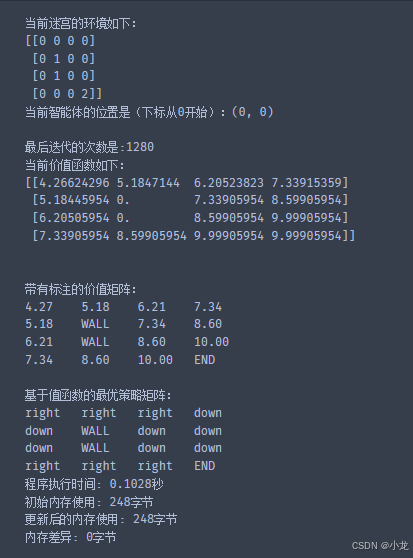
程序运行结果:
7. 总结
马尔可夫决策过程为我们提供了一个有力的工具来解决迷宫游戏中的路径规划问题。通过定义状态空间、动作空间、转移概率、奖励函数和折扣因子,我们可以使用动态规划方法,如价值迭代,求解最优策略,从而帮助智能体找到从起点到终点的最佳路径。这种方法不仅适用于迷宫问题,还可以广泛应用于其他需要优化决策的环境中。
























 300
300

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








