DirectX11坐标变换的理解

一、线性变换

1.缩放

通过龙书第三章的讲解，缩放矩阵为：

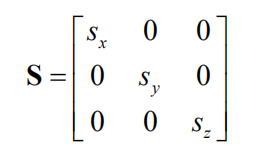
如何理解缩放矩阵呢，我们通过一个例子来加深印象：

假设一个向量是(2, 4, 1),如何让其x轴放大2倍，y轴缩小2倍，z轴放大4倍呢？
如果设计一个矩阵，能够满足这个要求，那么这个矩阵应该是什么样子的？

假设这个矩阵为:
[x1, x2, x3]
[y1, y2, y3]
[z1, z2, z3]

目标向量的三个坐标(x,y,z)
x = 2x1 + 4y1 + 1z1 (让x轴放大2倍只需另x1 = 2, y1 = 0, z1 = 0)
y = 2x2 + 4y2 + 1z2 (让y轴缩小2倍只需另x2 = 0, y2 = 1/2, z2 = 0)
z = 2x3 + 4y3 + 1*z3 (让z轴放大4倍只需另x3 = 0, y3 = 0, z3 = 4)

得到缩放矩阵为：
[2, 0, 0]
[0, 1/2, 0]
[0, 0, 4]

缩放矩阵对应DirectXMath数学库中的：

XMMATRIX XM_CALLCONV XMMatrixScaling
(float ScaleX, float ScaleY, float ScaleZ);

2.旋转矩阵

旋转矩阵的证明比较繁杂，读者可以看龙书第三章。
旋转矩阵对应DirectXMath数学库中的：

XMMATRIX XM_CALLCONV XMMatrixRotationX(float Angle);
XMMATRIX XM_CALLCONV XMMatrixRotationY(float Angle);
XMMATRIX XM_CALLCONV XMMatrixRotationZ(float Angle);

3.平移矩阵

平移矩阵的实际是对点进行平移，因为对向量进行平移是没有意义的。
因此博主将在仿射变换中进行讲解-往下看~~~

二、仿射变换

1.齐次坐标

在矩阵中我们定义向量为（x,y,z）
这个定义方便了我们进行旋转和缩放操作
但是现在问题是：当我们需要进行平移怎么办？

在通常的理解里，向量的平移是没有意义的，因为平移后的向量和原来的向量是相等的。因此为了实现从世界坐标中的一个位置将图形位移到另一个位置，或者局部坐标向世界坐标的变换，我们的做法是对局部坐标的原点进行平移。也就是 对点进行平移。

为了能够区分向量和点
我们在（x,y,z）的基础上添加了第四个分量w,即（x,y,z,w）
其中：
（x,y,z,0）表示向量
（x,y,z,1）表示坐标
这种表示方式就称之为齐次坐标

2.仿射变换矩阵

因为现在向量和坐标都是四维的，因此理所当然我们的变换矩阵也会变成4*4的矩阵

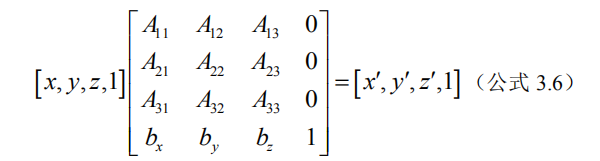
2.1简单分析

2.1.1第四列

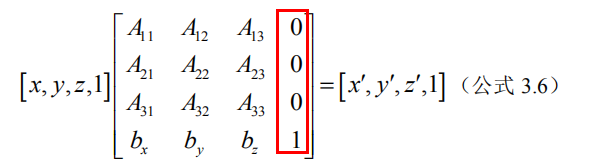
为什么第四列为0 0 0 1？
对第四列左右进行运算就知道，x0+y0+z0+11 = 1
这样得到的结果第四个分量永远都等于原来的第四个分量
比如原来的坐标为[x,y,z,0]，那么得到的结果就是[x’,y’,z’,0]

2.1.2第四行

现在我们观察一下第四行，[bx,by,bz,1]，这又代表什么呢？
我们分两种情况讨论：

1. 向量：向量的第四个坐标是0，那么和[bx,by,bz,1]相乘都是0，也就是对x,y,z坐标不产生影响。
2. 点：点的第四个坐标是1，那么和[bx,by,bz,1]相乘的结果是[bx,by,bz,1]，那么这个结果会和原本对X，Y，Z的运算结果进行分量相加。也就是说对x,y,z坐标进行移动。这就达到了对点进行平移，而对向量不产生影响的效果了。

2.2平移矩阵

如果没有旋转和缩放

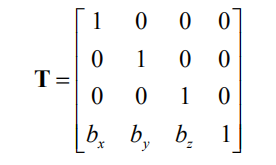
那么这个矩阵就称之为平移矩阵

很容易想到：如果不想要平移，只要将bx,by,bz设为0即可

3.从局部坐标向世界坐标的变换

假设我们现在在局部坐标轴上面建立了自己的图形，那么我们如何将其变换到世界坐标系呢？
有了上面仿射变换的理解，接下去的操作就简单很多了。我们通过龙书上面的一道例题来进行理解：

假设一个正方形的顶点局部坐标在(−0.5,0,−0.5)和(0.5,0,0.5)之间，将它的边长变为 2， 顺时针旋转 45°，并放置在世界空间的（10,0,10）坐标上，那如何求它在世界空间中的坐标 呢？

我们需要构建 S，R，T 矩阵，世界矩阵 W 如下所示：

上面的W = SRT称为组合变换，通过矩阵乘法将旋转、平移、缩放整合成一个组合变换矩阵，这样就可以避免多次变换，提高性能。

我们对这种变换有两种理解：
1.在局部坐标轴上进行旋转缩放，并且将局部坐标轴的原点移动到世界坐标轴的某个位置（如本题中的10,0,10）
2.先将局部坐标轴×单位世界矩阵，这相当于变换前的局部坐标原点位于世界坐标原点，然后对改图形的世界坐标进行旋转、缩放和平移。

三、物体的世界矩阵的理解

通常情况下，为了便于理解，我们总是将物体的中心（或者几何边界）放在局部空间的原点处，并以中心作为基准描述整个图形。

比如正方体，我们通常将几何中心放在原点，然后对称的标记其他顶点。
并且，这些顶点一般会是和x,y,z轴向对称的，这样方便后续的线性变换。

1.物体在世界坐标系中的移动

在局部空间绘制好顶点后，我们可以把这些顶点完全相同的复制到世界空间中。
也就是说在世界空间中，物体的初始状态是在原点的。
现在思考一个问题，如何让物体移动起来呢？

1.1 平移

我们设立一个物体的世界变换矩阵 m_World，让这个世界变换矩阵变为平移矩阵，然后再绘制前将物体的局部坐标*世界变换矩阵，就可以达到平移的目的。

1.2 旋转

让物体绕着几何中心旋转，要特别注意变换的先后顺序，一般情况下我们会先旋转再平移，如果需要两次对中心进行旋转，也要注意两次先后旋转的顺序。

比如一个长方体，先绕X轴旋转再绕Y轴旋转，或者先绕Y轴旋转再绕X轴旋转的结果是不同的。

1.3 缩放

缩放和上面类似，同样是获得一个变换矩阵罢了。

1.4 组合

我们最后获得的世界矩阵只有一个，如果一个物体需要经过平移、旋转、缩放的多个变换，只需要将这些矩阵按照正确的顺序进行相乘，获得的最终矩阵就是他的世界变换矩阵。
思考一个问题
假设一个物体有自己的前后左右方向，我们在经过旋转之后，怎么获得他变换后的正方向呢？
为了这个目的，我们需要理解物体的世界矩阵。
假设一个物体的中心处于原点，他的世界变换矩阵为：
(1, 2, 3, 0)
(3, 1, 2, 0)
(2, 1, 1, 0)
(1, 2, 2, 1）

假设物体look = Z轴，right = X轴， up = Y轴

第一行：(1, 2, 3)实际上是变换后物体的right轴
第二行：(3, 1, 2)实际上是变换后物体的up轴
第三行：(2, 1, 1)实际上是变换后物体的look轴
第四行：(1, 2, 2)是对向量(x，y，z)平移的距离

我们假设look轴为物体的正方向

那么我们只需要获得变换后的世界矩阵，并且得到前三行的前三个坐标，那么就可以更新look,right,up三个轴。
如果要让物体朝着正方向前进，则使用一个常用函数：XMVectorMultiplyAdd()

其中Dist是前进距离
Front是前进方向
Pos是初始坐标
XMVectorMultiplyAdd(Dist, Front, Pos)获得位移后的向量坐标。

这个原理可以帮助我们解决很多实际的问题，比如小车的第三人称移动。