GNN 笔记1 图的概念

UQI-LIUWJ

已于 2022-09-03 16:19:40 修改

阅读量1.2k

点赞数 3

分类专栏： GNN 文章标签：有向图图论

于 2021-06-19 15:55:45 首次发布

本文链接：https://blog.csdn.net/qq_40206371/article/details/118054195

版权

GNN 专栏收录该内容

9 篇文章

订阅专栏

1 图的定义

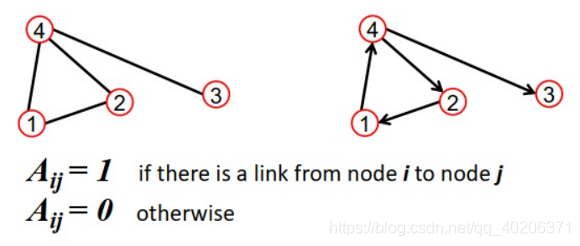
上图中的邻接矩阵分别为

$A_{left}= \begin{pmatrix} 0 & 1 & 0 &1 \\ 1 & 0 & 0 &1 \\ 0 & 0 & 0 &1 \\ 1 & 1 &1 & 0 \end{pmatrix} \quad \quad A_{right}=\begin{pmatrix} 0 & 0 & 0 &1 \\ 1 & 0 & 0 &0 \\ 0 & 0 & 0 &0 \\ 0 & 1 &1 & 0 \end{pmatrix}$

2 图的度

无向图的度就是，每个点和几个其他的点相连接，那么这个点的度就是几。

以上左图为例，点1的度为2，点4的度为3

有向图分为出度和入度，就是射出去和射进来的射线的数量

以上右图为例，点1的出度和入度都是1，点4的出度是2，入度是1

3 图的连通性

3.1 无向图的连通性

对于一个无向图，如果图中任意一个节点i可以通过一些边到达节点j，那么这个无向图具有连通性，我们称这个无向图为连通图。

换句话说，这个无向图没有孤立的节点。

3.1.1 连通分量

无向图G的一个极大连通子图被称为G的一个连通分量（或者叫连通分支）。

连通图只有一个连通分量（即自身）

非连通的无向图可能有多个连通分量

3.2 有向图的连通性

3.2.1 强连通性

给定图G=(V,E)，给定图G中任意两个节点u和v，如果结点u和v相互可达（也就是至少存在一条路径从u到v，也存在一条路径从v到u），那么这个有向图G具有强连通性，是强连通图。

3.2.2 弱连通性

如果至少有一对节点不满足互相联通（即这个有向图不具备强连通性），但是去掉边的方向后，从无向图的角度看，又是连通图，这样的有向图是弱连通图。

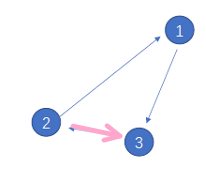
比如上一张图，我把3->2的射线改成2->3的射线，那么此时的有向图是弱连通图

4 图的直径

两两节点之间最短路径的最大值称之为直径

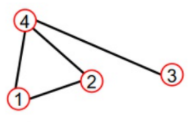
以这张图为例，图的直径为2（1->3）

5 度中心性

度中心性= $\frac{N_{degree}}{n-1}$

以这张图为例，点1的图中心性为2/(4-1)=2/3；点4 的图中心性为3/(4-1)=1

6 特征向量中心性

对于图的邻接矩阵A，我们对A求特征值和特征向量

最大特征值对应的特征向量，每一个维度对应这个点的特征向量中心性

特征向量取个反方向也没有影响。

7 中介中心性

以王者荣耀魏势力的人物关系图为例

这个分式怎么看呢？我们以曹操的中介中心性为例：

我们先看分母：任意两个节点，两两之间有一条最短路径（那么就是1）。除了曹操之外，还有五个点，五个点之间两两相连那么就还有5*4=20条最短路径.

然后我们看分子：

1）第一个括号：(0+1+1+0.5)

蔡文姬-甄姬，没有经过曹操，故为0

蔡文姬-司马懿，经过曹操，且只有一条路径，故为1

蔡文姬-夏侯惇，经过曹操，且只有一条路径，故为1

蔡文姬-典韦，有两条最短路径，其中一条经过曹操，故为0.5（占比）

2）第二个括号：（0+0+1+1）

甄姬-夏侯惇：经过曹操，且只有一条路径，故为1

甄姬-司马懿：经过曹操，且只有一条路径，故为1

甄姬-典韦：没有经过曹操，故为0

甄姬-蔡文姬：没有经过曹操，故为0

3）第三个括号：（0+1+1+0.5）

典韦-夏侯惇：经过曹操，且只有一条路径，故为1

典韦-司马懿：经过曹操，且只有一条路径，故为1

典韦-甄姬：没有经过曹操，故为0

典韦-蔡文姬：有两条最短路径，其中一条经过曹操，故为0.5（占比）

4）第四个括号：（1+1+1+1）

司马懿-夏侯惇：经过曹操，且只有一条路径，故为1

司马懿-蔡文姬：经过曹操，且只有一条路径，故为1

司马懿-典韦：经过曹操，且只有一条路径，故为1

司马懿-甄姬：经过曹操，且只有一条路径，故为1

5）第五个括号：（1+1+1+1）

夏侯惇-司马懿：经过曹操，且只有一条路径，故为1

夏侯惇-典韦：经过曹操，且只有一条路径，故为1

夏侯惇-蔡文姬：经过曹操，且只有一条路径，故为1

夏侯惇-甄姬：经过曹操，且只有一条路径，故为1

8 连接中心性

还是以刚才那个图为例：

9 拉普拉斯矩阵

拉普拉斯矩阵（Laplacian matrix)），也称为基尔霍夫矩阵, 是表示图的一种矩阵。给定一个有n个顶点的图，其拉普拉斯矩阵被定义为:L=D−W 其中D为图的度矩阵，W为图的邻接矩阵。

以下图为例：

邻接矩阵
度矩阵
拉普拉斯矩阵

9.1常见的几种拉普拉斯矩阵

combinatorial Laplacian/ Vanilla Laplacian

L=D-A

Symmetric normalized Laplacian

$L^{s}=D^{-0.5}LD^{-0.5}$

（很多GCN的论文中，使用的就是这种拉普拉斯矩阵）

Random walk normalized Laplacian

$L^R=D^{-1}L$

9.2 拉普拉斯矩阵的性质

拉普拉斯矩阵是半正定对称矩阵

而实对称矩阵的性质有：

一定有n个线性无关的特征向量
这n个特征向量总是可以化成两两相互正交的正交矩阵

半正定矩阵的性质为：特征值一定非负