算法笔记：ARIMA，时间序列平稳性

1 平稳性

        平稳性要求经由样本时间序列所得到的拟合曲线，在未来的一段时间内，仍然能按照现在的特征，顺着现在的惯性继续延续下去

        平稳性要求时间序列的均值和方差不能发生明显的变化（可以变化，不能明显的变化）【换言之，这个时间序列和事件无关；时间序列不是时间的一个函数】

        如果时间序列的性质随着时间的偏移，发生了很大的变化（即不满足平稳性），那么传统时间序列方法这种学习历史数据意义就不大了

1.1 严平衡与弱平衡

1.1.1 严平衡：

        时间序列的分布不随时间的改变而改变

        也就是均值和方差严格相同

        这种要求太过绝对，在实际的数据中不太常见

        

1.1.2 弱平衡：

        时间序列的期望与相关系数不变

        

(期望：对于所有的时刻t，有E[vt]=μ，其中μ是一个常数。)

(相关系数：对于所有的时刻t和任意的间隔k，值之间的协方差,其中γk与时间t无关。他仅仅依赖于时间间隔k）

        相关系数即依赖性，未来某一时刻t的值要依赖于它过去的一些信息，这个依赖关系就是一种相关系数

         弱平衡在实际的数据中反而会更常见一点

1.1.3 平衡性检验

• 时序图
  • 如果是平稳的，值会围绕一个均值上下波动
• 自相关图
  • 平稳序列要求自协方差不受时间影响，只与时间差有关
  • 所以平稳时间序列的自相关图会随着阶数的递增，自相关函数会降到0附近，反之则可能是非平稳时间序列了
  • 

• 将时间序列分为2个或者多个连续片段，然后计算对应的统计量（比如均值、方差、自相关系数等），如果片段的统计量都是明显不相等的话，说明肯定不是平稳性。

1.2 差分法

        数据可能本身的浮动很大，但是经过差分（一阶、二阶、。。。多阶）之后，可能会呈现一定的平稳性。         

        

        在pandas中，比如pd['idx'].diff(x)，就会计算pd表格’idx'条目中的x阶差分 

2 ARIMA 模型

2.1 自回归模型（AR)

        回归模型我们都知道，用一组值来预测一个

        但是对于时间序列问题来说，我们没有变量-变量对，所以用不了回归模型。

        但是我们有当前值和历史值，所以我们可以通过描述当前值和历史值之间的关系，用变量自身的历史时间序列数据对自己预测，形成自回归。

        自回归模型必须满足平稳性的要求。

        p阶自回归过程的公式为：

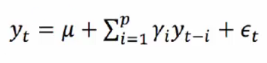
        其中：

• yt是当前值
• μ是常数项 
• p是阶数，表示今天的数据可能会收到过去p天内时间序列数据的影响（所以这里是一个Σ求和的操作，表示综合考虑了过去p天的信息）。这个p的值需要自己指定
• γi表示过去第i天的自相关系数，也是ARIMA需要学习的系数
• εt表示当前时刻的误差

        

2.1.2 自回归模型的限制

•         自回归模型使用自身的数据来进行预测
•         自回归模型研究的时间序列数据必须具有平稳性
•         自回归模型研究的数据必须有自相关性，如果自相关系数小于0.5，那么不宜使用自回归模型
  • 如果两个时间序列完全一样，那么他们的自相关系数就是自相关系数的最大值1
  • 如果两个时间序列完全相反，那么他们的自相关系数就是自相关系数的最小值-1
  • 综合来说，自相关系数的取值范围为[-1,1]
•          自回归模型只能预测与自身历史时间序列特征相似的内容

2.1.3 自回归模型最优解

首先，我们对自回归模型的线性表达式进行改写：

原来是：

现在改写为:

 

 

 将y合并，有：

其中 

 

 

 使用最小二乘法，求解回归系数α的最优解：

2.2 移动平均模型

        移动平均模型关注的是自回归模型中误差项的累加

         相当于对之前q天的误差进行一个加权求和

        移动平均法可以减少预测数值的突变，有效消除时间序列预测问题中的随机波动

2.3 ARMA

        自回归移动平均模型

        

        自回归与移动平均的结合

        我们这里p和q是需要事先指定的，γ和θ是需要学习的

2.4 ARIMA

        autoregressive integrated moving average model

        全称为差分自回归移动平均模型，写作ARIMA(p,d,q)

                AR是自回归，p是自回归项数（需要加权计算多少天之前的时间序列数据）

                MA是移动平均，q是移动平均项数（需要加权计算多少天之前的误差数据）

                I表示差分，d为时间序列变得平稳的时候，所需要做的差分次数

        原理：

                1，将非平稳时间序列转化成平稳的时间序列

                2，当前数值只受一定范围内的历史数据和一定范围内的误差值的影响

3 ARIMA的评估方法

3.1 自相关函数ACF（autocorrelation fuction）

3.1.1 自协方差 

不同时点的变量之间的协方差

 

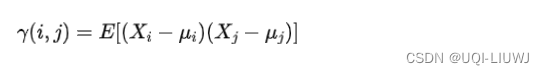
3.1.2 自相关函数

                自相关函数反映了同一序列在不同时点的变量之间的相关性【时间序列和它自己滞后n阶时序数据的相关性】

                这里表示k时刻之前的时间序列数据和当前时间序列数据之间的相关性

                ACF的取值范围是[-1,1]

                

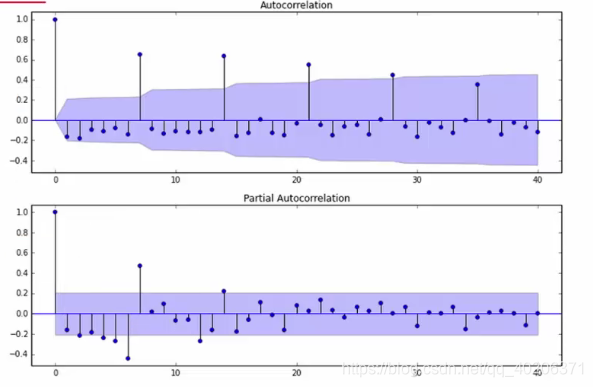
                如上图，就是一时间序列数据的ACF图。两条紫色序列表示它的置信区间（百分之多少的点落在这个区间之内）

• 正自相关系数——现在的高价值有可能在未来产生高价值
• 负自相关系数——今天的高价值意味着明天的低价值，今天的低价值意味着明天的高价值

 3.2 偏自相关函数（PACF partial autocorrelation function）

        对于一个平稳的自回归模型AR(p)，求出k之后自相关系数ACF(k)的时候，实际上得到的并不是x(t)和x(t-k)之间单单纯纯的相关关系。

        x(t)同时还会受到t-k~t之间k-1个随机变量x(t-1)....x(t-k+1)的影响。这些变量都和x(t-k)有一定程度的相关关系

        所以自相关系数ACF中其实还糅杂了其他变量对x(t),以及x(t-k)对这几个变量的影响。

        PACF则是严格表示了两个变量之间的相关性

4 ARIMA的p，d，q的确定

 其中截尾表示落在置信区间内的意思。

AR(p)看PACF，MA(q)看ACF

 4.1 ARIMA 建模流程

        1，将时间序列平稳化：通过差分法确定d的大小

        2，通过ACF或者PACF确定p和q的阶数

        3，计算ARIMA(p,d,q)

4.2 模型选择

4.2.1 AIC 赤化信息准则（Akaike information criterion）

        

其中 k为模型参数的个数，L为模型的似然函数

我们的目标是让AIC越小越好，也就是模型的参数越少越好（模型越简单越好），同时模型的似然函数越大越好（最大似然估计）

4.2.2 BIC 贝叶斯信息准则（Bayesian information criterion）

 其中k为模型参数的个数，n为样本数量，L为模型的似然函数

在相同输入样本的时候，BIC所表达的意义和AIC是一样的