卫星轨道知识总结

宇宙速度

三大宇宙速度的推导 - 知乎 (zhihu.com)

第一宇宙速度（环绕速度）：7.9 km/s。物体在地面附近绕地球做匀速圆周运动的最小发射速度。卫星飞行的水平速度即第一宇宙速度，卫星一旦该速度，不需要额外动力即可环绕地球飞行。此时卫星的 飞行轨迹 叫卫星轨道。

第二宇宙速度（逃逸速度）：11.2 km/s。物体挣脱地球引力束缚，离开地球的最小发射速度。

第三宇宙速度：16.7 km/s。物体挣脱太阳引力的束缚，离开太阳系的最小发射速度。

第四宇宙速度：约 110-120 km/s。物体摆脱银河系引力束缚，飞出银河系的最小发射速度。

第五宇宙速度：物体飞出本星系群的最小发射速度，由于本星系群的半径和质量均未有足够精确数据，因而无法准确得知大小。估计本星系群大小为500-1000光年，照这样计算，至少需要1500-2250km/s 的发射速度才能飞离。

第六宇宙速度：假设宇宙之外还有别的世界，要摆脱宇宙到达另一个世界，需要的最小发射速度。目前还不知道该宇宙速度是否存在。

卫星轨道参数

        卫星在地球引力等各种力的作用下做周期运动，一阶近似是一个开普勒椭圆轨道。由于其他力的存在（比如 地球的形状，大气阻力，其他星球的引力...），实际的轨道和理想的开普勒轨道有偏离，这个在航天里称为“轨道摄动”。

        长轴 和 短轴 决定 卫星轨道的形状和大小。交点角 Ω 、近地点幅角 ω 、轨道倾角 i  决定 轨道在空间的方位。这五个参数称为卫星轨道要素（根数）。加上 近地点时刻 tp ，合称为六要素。通过六要素可以确定 任何时刻卫星在空间的位置。

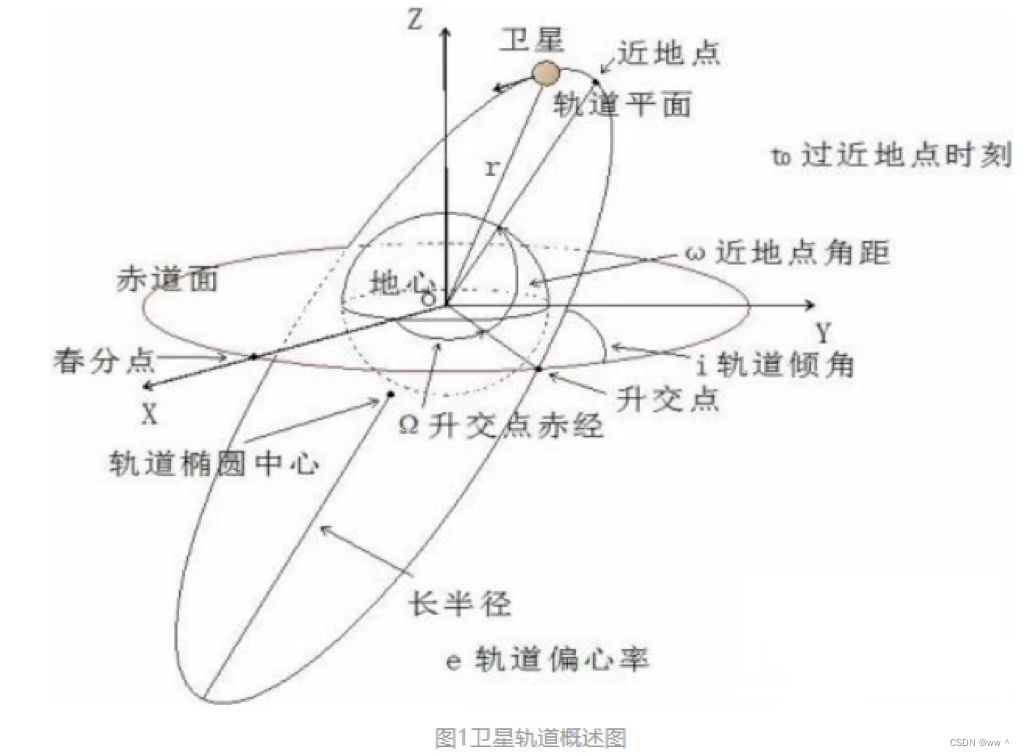
近地点角 ω ：在轨道平面内升交点和近地点与地心连线间的夹角。

轨道倾角 i ：地球赤道平面与卫星轨道平面间的夹角。

平均近交点：若卫星通过近地点的时刻为 tp，卫星的平均角速度为N，则任一时刻的平均近点角为 M = N ( t - tp )。

星下点：卫星与地球中心连线在 地球表面 的交点。

升交点：卫星 由南往北 飞行时，飞行轨迹在 赤道 上的交点。

周期：卫星绕地球一周的时间。

载距：卫星绕地球一周，地球转过的度数。

卫星轨道高度

高度：卫星离地球表面的距离。轨道越高，轨道半径越大，线速度越小，角速度越小。

低轨道：200～2000 km。中轨道：2000～20000 km。高轨道：＞ 20000 km。

        由于空气阻力的作用，高度小于120km的卫星会掉下来。例：美国1959年发射的一颗卫星，距地球最低点是112Km，这颗卫星发射得很成功，但上去围绕地球转了一圈后就掉下来了。

典型的卫星轨道

地球同步轨道

        运行周期等于地球自转周期（23小时56分4秒）的顺行轨道（运行方向与地球自转方向相同）。其 星下点轨迹为 8 字形。对地面观测者而言，每天相同时刻卫星出现在相同的方向上。

地球静止轨道

       轨道倾角为 0° 的 圆形（轨道偏心率为 0）地球同步轨道。

SAR卫星 的 升降轨 & 左右视

概念

升轨：卫星从 地球南极 向 地球北极 运动。（升轨 = 从南向北 = 从下往上）

降轨：卫星从 地球北极 向 地球南极 运动。

左视：卫星拍摄方向 为 卫星前进方向 的 左边。（看左边 = 从右向左看）

右视：卫星拍摄方向 为 卫星前进方向 的 右边。

卫星拍摄方向 = 斜距向 (slant range) ， 卫星前进方向 = 方位向 (azimuth) 。

理解

        SAR 成像的特点是 距离近的先接收到回波 。

        升轨时，从下往上拍，成像时 先记录下面、再记录上面，最终效果会 与实际地物上下颠倒。降轨 时，与实际地物的上下顺序一致。

        从东往西拍 (西视) 时，先记录东面、再记录西面，最终效果会与实际左右颠倒 (左西右东)，即 升轨时的左视、降轨时的右视。反之，从西往东拍 (东视 )，即 升轨时的右视、降轨时的左视，最终成像效果与实际地物的左右顺序一致。

        总结： 降轨左视与实际地物上下左右完全一致， 降轨右视 左右颠倒， 升轨右视 上下颠倒，升轨左视 上下左右都颠倒（中心倒置）。