laplace-beltrami operator 是 laplace operator在riemann manifolds上的拓展. 至于他们两到底有什么区别和联系,请看[2]中的一段话:

可以看到, laplace-beltrami operator与普通laplace operator的区别就在于一个metric G,那么这个metric G究竟是个什么东西?
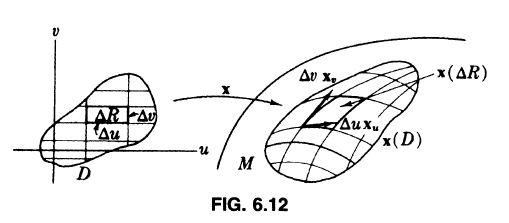
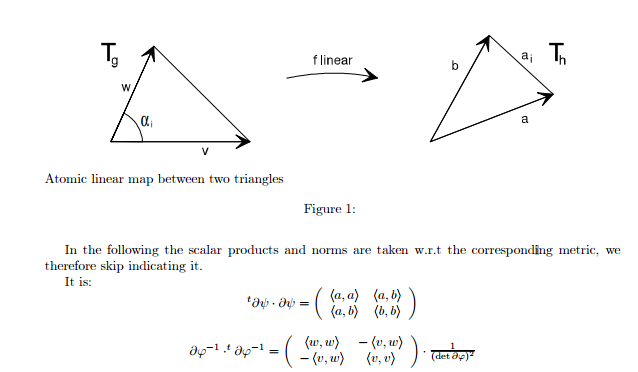
注意这里的局部坐标系底面的两个轴方向是由Xu,Xv(在该点的切平面中)的点乘为多少?
这样我们就引入了First fundamental form
所以,对于局部坐标系下的两个向量x,y相乘, 他们的积应该表示为如上所示.
所以矩阵
这里我们看下[5]中关于metric的定义

所以G也就是[1]中所讲的
也是[4]中所讲的
以及[3]中所讲的
注意这里的G. 在[2]中有所提到
这里我想多说一下导数的问题, ∀u∈Rn
如果把这种情况扩展到Riemann几何上那么就需要把普通意义下的向量映射到该点的切平面内, 而这个映射就是J=df
所以du就得到我们想到的了.
关于[2]中所描述的da=g√du1…dun, 我们先看下[4]中的二维下的情况
运用到三维及以上就得证, 其中g√在三维情况下就是变化的体积
reference:
[1]Laplace-Beltrami operator Diffusion geometry
[2]Conformal Mapping with as Uniform as Possible Conformal Factor
[3]Computing discrete minimal surfaces and their conjugates
[4]First fundamental form
[5]Elementary Differential Geometry
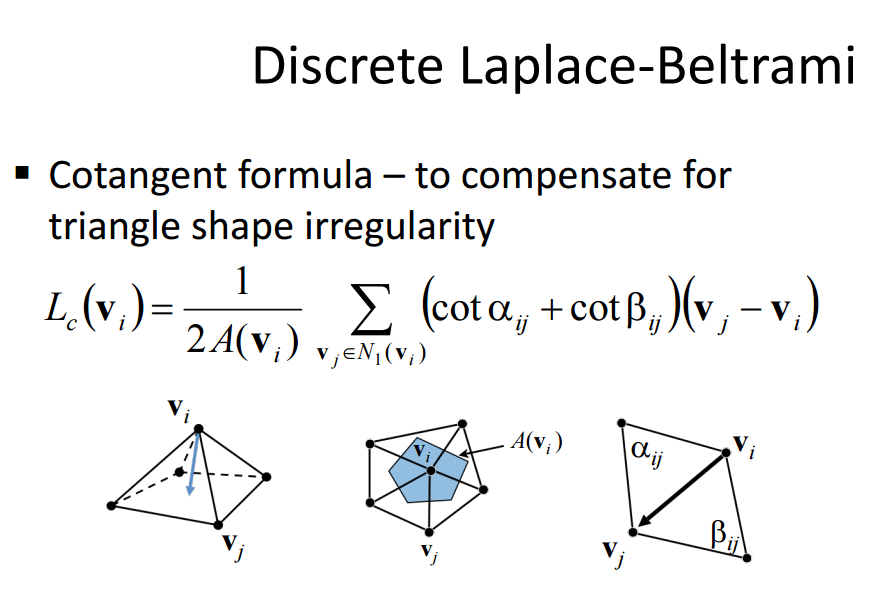
关于离散的请好好看下以下资料
http://webcourse.cs.technion.ac.il/236861/Winter2013-2014/ho/WCFiles/laplace_beltrami.pdf
https://igl.ethz.ch/projects/deformation-survey/eg09_tutorial_slides.pdf
https://people.eecs.berkeley.edu/~jrs/meshpapers/MeyerDesbrunSchroderBarr.pdf
http://ac.els-cdn.com/S0097849309000272/1-s2.0-S0097849309000272-main.pdf?_tid=665c5518-d8b9-11e6-84f6-00000aab0f6c&acdnat=1484220328_c210ff0d8bcd2b9277aebb981df8280d










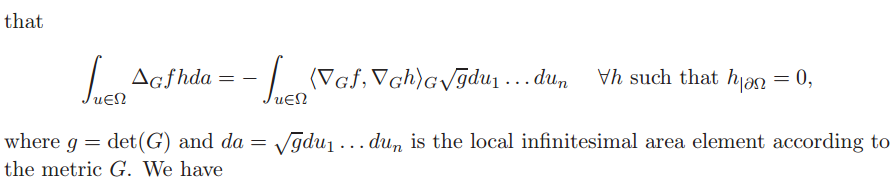

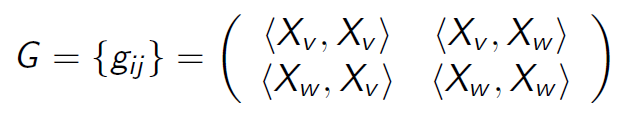


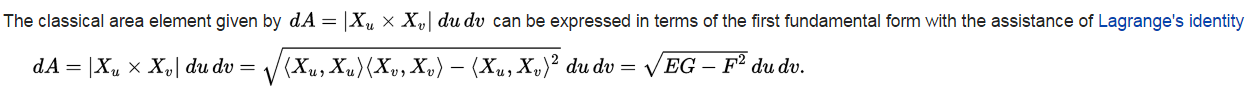
















 208
208

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








