【视觉slam十四讲实战】

安装Ubuntu

不想安装双系统，不想安装虚拟机，没有独立硬盘，可以使用应用商店里的

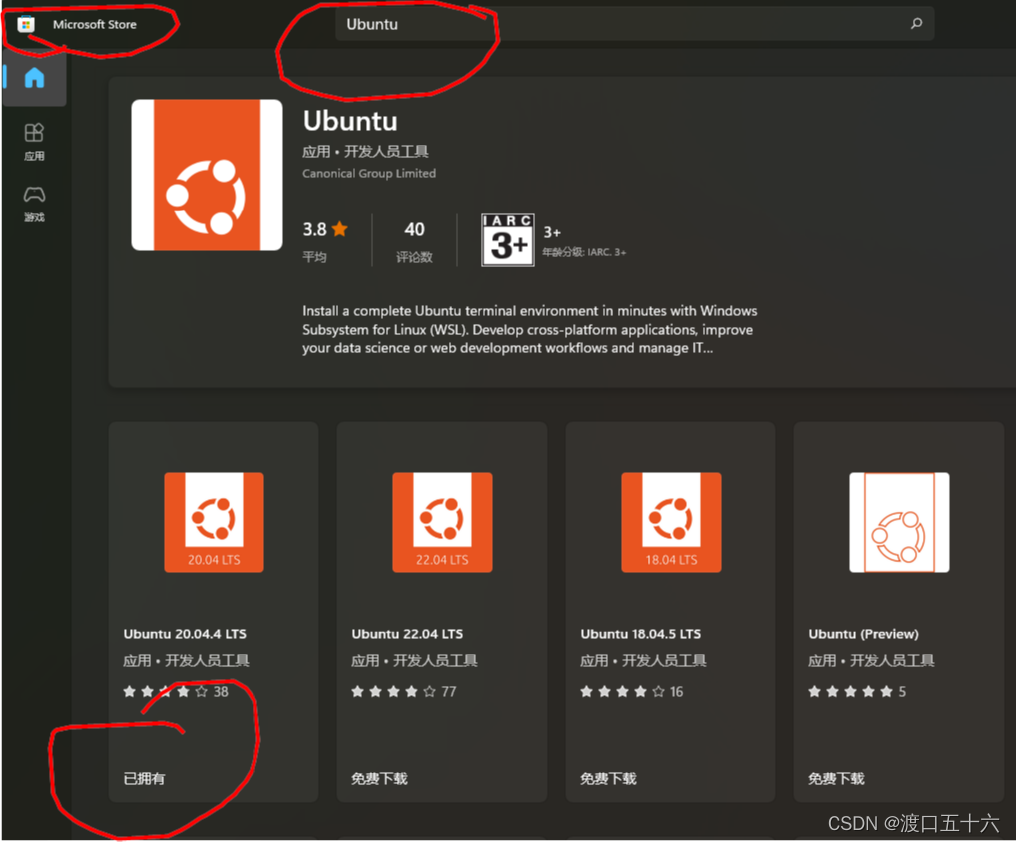
报错 Installing, this may take a few minutes… WslRegisterDistribution failed with error: 0x800701bc

解决办法，按照教程一步一步来，请点我哦

之后输入用户名和密码

编程基础

安装g++

sudo apt updata
suda  apt-get install g++

编写第一个程序 helloSLAM.cpp

#include <iostream>
using namespace std;
int main( int argc, char** argv )
{
	cout<<"Hello SLAM!"<<endl;
	return 0;
}

g++编译

g++ helloSLAM.cpp

运行程序

./a.out

使用 cmake编译

安装cmake

sudo apt-get install cmake

编写CMakeLists.txt

#  声明要求的 cmake 最低版本
cmake_minimum_required(VERSION 2.8)

 # 声明一个 cmake 工程
project(hellow)

 # 添加一个可执行程序
# 语法：add_executable( 可执行程序名 源代码文件 ）
add_executable(hello  hellowSlam.cpp) # 中间用空格隔离                        

CMakeLists.txt 和 hellowSlam.cpp是在同一目录，然后在当前目录下对该工程分析

cmake.
make
./可执行程序名   # 执行程序

为了能够更快删除生成的文件，创建一个build文件夹

mkdir build
cd build
cmake ..
make

将自己写的方法编译成库

//name:libHelloSLAM.cpp
//这是一个库文件
#include <iostream>
using namespace std;
void printHello()
{
	cout<<"Hello SLAM"<<endl;
}

我们在 CMakeLists.txt 里加一句：

add_library( hello libHelloSLAM.cpp)

编译

cd build
cmake ..
make

这时，在 build 文件夹中会生成一个 libhello.a 文件，这就是我们得到的库。

静态库和动态库

在 Linux 中，库文件分成静态库和共享库两种①。静态库以.a 作为后缀名，共享库以.so结尾。所有库都是一些函数打包后的集合，差别在于静态库每次被调用都会生成一个副本，而共享库则只有一个副本，更省空间。如果我们想生成共享库而不是静态库，只需用：

add_library( hello_shared SHARED libHelloSLAM.cpp )

库文件是一个压缩包，里头带有编译好的二进制函数。不过，仅有.a 或.so 库文件的话，我们并不知道它里头的函数到底是什么，调用的形式又是什么样的。为了让别人（或者自己）使用这个库，我们需要提供一个头文件，说明这些库里都有些什么。因此，对于库的使用者，只要拿到了头文件和库文件，就可以调用这个库了。下面我们来写 libhello 的头文件。

//name:libHelloSLAM.h
#ifndef LIBHELLOSLAM_H_
#define LIBHELLOSLAM_H_
void printHello();
#endif

这样，根据这个文件和我们刚才编译得到的库文件，就可以使用这个函数了。下面我们写一个可执行程序，调用这个简单的函数：

使用库

//name:useHello.cpp
#include "libHelloSLAM.h"
int main( int argc, char** argv )
{
	printHello();
	return 0;
}

然后，在 CMakeLists.txt 中添加一个可执行程序的生成命令，链接到刚才我们使用的库上：

add_executable( useHello useHello.cpp )
target_link_libraries( useHello hello_shared )

linux的免费IDE(Kdevelop桌面版)

第三讲 三维空间刚体运动

目标：
理解三维空间的刚体运动描述方式：旋转矩阵、变换矩阵、四元数和欧拉角。
掌握 Eigen 库的矩阵、几何模块使用方法。
请不要把向量与它的坐标两个概念混淆。一个向量是空间当中的一样东西，比如说 a。这里 a 并不是和若干个实数相关联的。只有当我们指定这个三维空间中的某个坐标系时，才可以谈论该向量在此坐标系下的坐标，也就是找到若干个实数对应这个向量。例如，三维空间中的某个向量的坐标可以用 R3 当中的三个数来描述。某个点的坐标也可以用 R3来描述。怎么描述的呢？如果我们确定一个坐标系，也就是一个线性空间的基 (e1, e2, e3)，那就可以谈论向量 a 在这组基下的坐标了：

所以这个坐标的具体取值，一个是和向量本身有关，第二也和坐标系的选取有关。

向量的外积a x b = a ^ b

坐标系间的欧氏变换

在机器人的运动过程中，常见的做法是设定一个惯性坐标系（或者叫世界坐标系），可以认为它是固定不动的，例如图中的 xW , yW , zW 定义的坐标系。同时，相机或机器人则是一个移动坐标系，例如 xC , yC , zC 定义的坐标系。我们会问：相机视野中某个向量 p，它的坐标为 pc，而从世界坐标系下看，它的坐标 pw。这两个坐标之间是如何转换的呢？这时，就需要先得到该点针对机器人坐标系坐标值，再根据机器人位姿转换到世界坐标系中，这个转换关系由一个矩阵 T 来描述，如图 3-2 所示。

相机运动是一个刚体运动，它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化。这种变换称为欧氏变换。想象你把手机抛到空中，在它落地摔碎之前，只可能有空间位置和姿态的不同，而它自己的长度、各个面的角度等性质不会有任何变化。这样一个欧氏变换由一个旋转和一个平移两部分组成。首先来考虑旋转。我们设某个单位正交基(e1, e2, e3) 经过一次旋转,变成了(e1’, e2’, e3’)。那么，对于同一个向量 a（注意该向量并没有随着坐标系的旋转而发生运动），它在两个坐标系下的坐标为

根据坐标的定义，有：

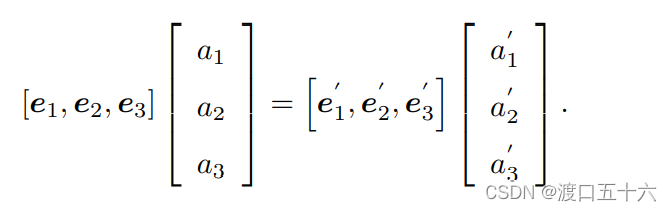
向量的长度和位置没变， 所以基向量乘以坐标是相等的。
为了描述两个坐标之间的关系，我们对上面等式左右同时左乘
那么左边的系数变成了单位矩阵，所以：

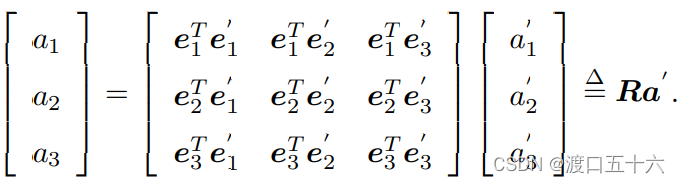
我们把中间的阵拿出来，定义成一个矩阵 R。这个矩阵由两组基之间的内积组成，刻画了旋转前后同一个向量的坐标变换关系。只要旋转是一样的，那么这个矩阵也是一样的。可以说，矩阵 R 描述了旋转本身。因此它又称为旋转矩阵。
旋转矩阵有一些特别的性质。事实上，它是一个行列式为 1 的正交矩阵①。反之，行列式为 1 的正交矩阵也是一个旋转矩阵。所以，我们可以把旋转矩阵的集合定义如下：R是基， det是行列式

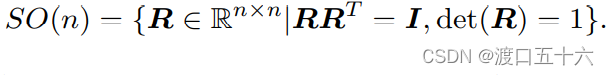
SO(n) 是特殊正交群（Special Orthogonal Group）的意思。这个集合由 n 维空间的旋转矩阵组成，特别的，SO(3) 就是三维空间的旋转了。通过旋转矩阵，我们可以直接谈论两个坐标系之间的旋转变换，而不用再从基开始谈起了。换句话说，旋转矩阵可以描述相机的旋转。
由于旋转矩阵为正交阵，它的逆（即转置）描述了一个相反的旋转。按照上面定义方式，有：

显然 RT 刻画了一个相反的旋转。
在欧氏变换中，除了旋转之外还有一个平移。考虑世界坐标系中的向量 a，经过一次旋转（用 R 描述）和一次平移 t 后，得到了a’, 那么把旋转和平移合到一起，有：

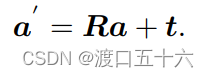
其中，t 称为平移向量。相比于旋转，平移部分只需把这个平移量加到旋转之后的坐标上，显得非常简洁。通过上式，我们用一个旋转矩阵 R 和一个平移向量 t 完整地描述了一个欧氏空间的坐标变换关系。

变换矩阵与齐次坐标

按照a’ = Ra + t的形式进行多次变换的时候会过于复杂。

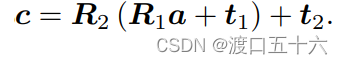
因此，我们要引入齐次坐标和变换矩阵重写式

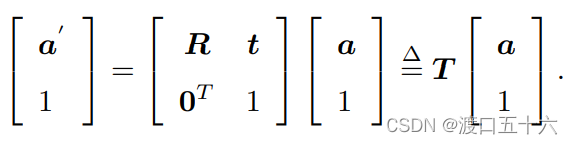
这是一个数学技巧：我们把一个三维向量的末尾添加 1，变成了四维向量，称为齐次坐标。对于这个四维向量，我们可以把旋转和平移写在一个矩阵里面，使得整个关系变成了线性关系。该式中，矩阵 T 称为变换矩阵（Transform Matrix）。我们暂时用 a˜ 表示 a 的齐次坐标。

实践：Eigen

Eigen①是一个 C++ 开源线性代数库。它提供了快速的有关矩阵的线性代数运算，还包括解方程等功能。许多上层的软件库也使用 Eigen 进行矩阵运算，包括 g2o、Sophus 等。
安装 Eigen

sudo apt-get install libeigen3-dev

旋转向量

有了旋转矩阵来描述旋转，有了变换矩阵描述一个六自由度的三维刚体运动，但是这种表示略显冗余，因为：SO(3) 的旋转矩阵有九个量，但一次旋转只有三个自由度。因此这种表达方式是冗余的。同理，变换矩阵用十六个量表达了六自由度的变换。那么，是否有更紧凑的表示呢？

我们可以使用一个向量，其方向与旋转轴一致，而长度等于旋转角。这种向量，称为旋转向量（或轴角，Axis Angle）。这种表示法只需一个三维向量即可描述旋转。同样，对于变换矩阵，我们使用一个旋转向量和一个平移向量即可表达一次变换。这时的维数正好是六维。

那么我们需要研究旋转向量和旋转矩阵的转换

假设有一个旋转轴为 n，角度为 θ 的旋转，显然，它对应的旋转向
量为 θn。由旋转向量到旋转矩阵的过程由罗德里格斯公式（Rodrigues’s Formula ）表明，

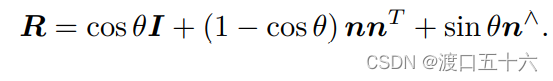
欧拉角

欧拉角则提供了一种非常直观的方式来
描述旋转——它使用了三个分离的转角，把一个旋转分解成三次绕不同轴的旋转。当然，由于分解方式有许多种，所以欧拉角也存在着不同的定义方法。比如说，当我先绕 X 轴旋转，再绕 Y 轴，最后绕 Z 轴，就得到了一个 XY Z 轴的旋转。同理，可以定义 ZYZ、ZYX等等旋转方式。如果讨论更细一些，还需要区分每次旋转是绕固定轴旋转的，还是绕旋转之后的轴旋转的，这也会给出不一样的定义方式。

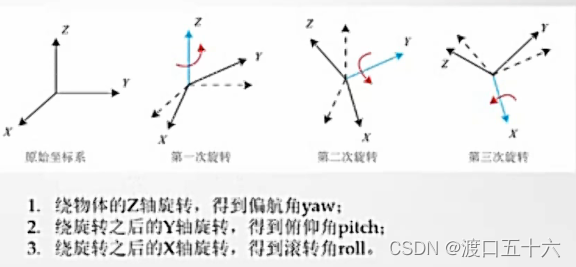
不实用， 因为存在万向锁的情况，具有奇异性，如下图第一次旋转和第三次旋转的效果是一样的（都是绕同一方向轴），所以间接的少了一个自由度

四元数

旋转矩阵用九个量描述三自由度的旋转，具有冗余性；欧拉角和旋转向量是紧凑的，但具有奇异性。事实上，我们找不到不带奇异性的三维向量描述方式 [19]。这有点类似于，当我们想用两个坐标表示地球表面时（如经度和纬度），必定存在奇异性（纬度为 ±90◦ 时经度无意义）。三维旋转是一个三维流形，想要无奇异性地表达它，用三个量是不够的。

未完待续