计算几何基础知识叉乘、点乘、点到直线距离、叉积方向法等

最新推荐文章于 2025-02-19 14:01:10 发布

长沙大学ccsu_deer

最新推荐文章于 2025-02-19 14:01:10 发布

阅读量6.2k

点赞数 5

分类专栏：计算几何--几何基础知识

本文链接：https://blog.csdn.net/qq_41286356/article/details/109595335

版权

计算几何--几何基础知识专栏收录该内容

1 篇文章

订阅专栏

本文介绍了计算几何中的关键概念和技术，包括点与直线位置关系的判断、向量的叉积和点积运算、线段相交判断及多边形面积计算等。通过具体的代码示例，帮助读者理解和应用这些几何计算方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、几何

常考却不怎么掌握的：

数据结构：分块

字符串：后缀数组、后缀自动机

数学：FFT、DFT、NTT、杜教筛、拉格朗日插值等

图论：网络流、最小费用最大流

动规：五边形数优化dp

1、判断一个点在一条直线的左侧还是右侧叉乘方向法

向量的叉积，p1,p2,p3三个点，判断p3在p1p2向量的左边还是右边，左右跟向量的方向有关，如果是p1p2的方向，那么就是对|p1,p2,p3|进行叉积计算，根据右手法则，如果计算的答案大于0，就是左侧，小于0就是右侧，等于0就是在直线上。

2、判断一个点是否在矩形内叉乘同向法

3、判断点是否在三角形内

假设点P位于三角形内，会有这样一个规律，当我们沿着ABCA的方向在三条边上行走时，你会发现点P始终位于边AB，BC和CA的右侧。我们就利用这一点。

但是如何判断一个点在线段的左侧还是右侧呢？我们可以从另一个角度来思考，当选定线段AB时，点C位于AB的右侧，同理选定BC时，点A位于BC的右侧，最后选定CA时，点B位于CA的右侧，所以当选择某一条边时，我们只需验证点P与该边所对的点在同一侧即可。

问题又来了，如何判断两个点在某条线段的同一侧呢？可以通过叉积来实现，连接AP，将AP和AB做叉积，再将AC和AB做叉积，如果两个叉积的结果方向一致，那么两个点p、c 在同一侧，同理另外两条边一样的计算方案。

判断两个向量的是否同向可以用点积实现，如果点积大于0，则两向量夹角是锐角，否则是钝角。

*注释：*为什么叉乘就可以判断方向性，因为叉乘是满足反交换律的，e= a x b = -b x a, 满足右手定则（按夹角为锐角，顺时针），顺时针由a到b，大拇指的方向就是e的方向，AP x AB 与 AC x AB 叉乘的结果是同向的，方向都是垂直三角形ABC这个平面朝上的，而AQ x AB 则是方向朝下，所以q和c不在同一侧；根据此原理就能判断一个点是否在一个三角形中。

二、计算几何基础整合(point类)

参考来自：博客

1、首先定义Point类：

const double eps=1e-8;

int dcmp(double x) {return fabs(x)<=eps?0:x>eps?1:-1;}

struct Point {
    double x,y;
    Point(double x=0,double y=0):x(x),y(y) {}
    Point operator + (const Point &a) {return Point(x+a.x,y+a.y);}
    Point operator - (const Point &a) {return Point(a.x-x,a.y-y);} //注意翻转！！
    Point operator * (double a) {return Point(x*a,y*a);}
    Point operator / (double a) {return Point(x/a,y/a);}
    bool operator < (const Point &b) const {return x<b.x||(x==b.x&&y<b.y);}
    bool operator == (Point b) {return dcmp(x-b.x)==0&&dcmp(y-b.y)==0;}
    double length() {return sqrt(x*x+y*y);}
    Point rotate(double rad) {return Point(x*cos(rad)-y*sin(rad),x*sin(rad)+y*cos(rad));} //逆时针
    Point normal(Point a) {return Point(-a.y/a.length(),a.x/a.length());} //长度归一
};

typedef Point Vector; //仅为了写法方便，但意义不同

值得注意的是，在重载减法的时候，为了代码方便将其反过来定义了，这样a−ba−b就表示a→ba→b这个向量。但如果要用到减法时请将它翻转回去。

类中定义了两个操作：

向量旋转

根据仿射变换，逆时针旋转α度时需要执行：
长度归一这是方向向量的一种定义方法，向量只有方向没有长度。

2、叉积点积，夹角以及三角形面积

double Cross(const Vector& a,const Vector& b) {return a.x*b.y-b.x*a.y;}
double Dot(Vector a,Vector b) {return a.x*b.x+a.y*b.y;}
double Angle(Vector a,Vector b) {return acos(Dot(a,b)/a.length()/b.length());}
double Area(Point a,Point b,Point c) {return Cross(b-a,c-a);}

3、判断p是否在线段上

通过叉积判断面积是否为0，也就是判断是否在直线上。通过点积判断投影是否小于0，也就是判断p到线段端点是否同向。

bool OnSegment(Point st,Point ed,Point p) {return dcmp(Cross(st-p,ed-p))==0&&dcmp(Dot(st-p,ed-p))<0;}

4、判断线段是否相交

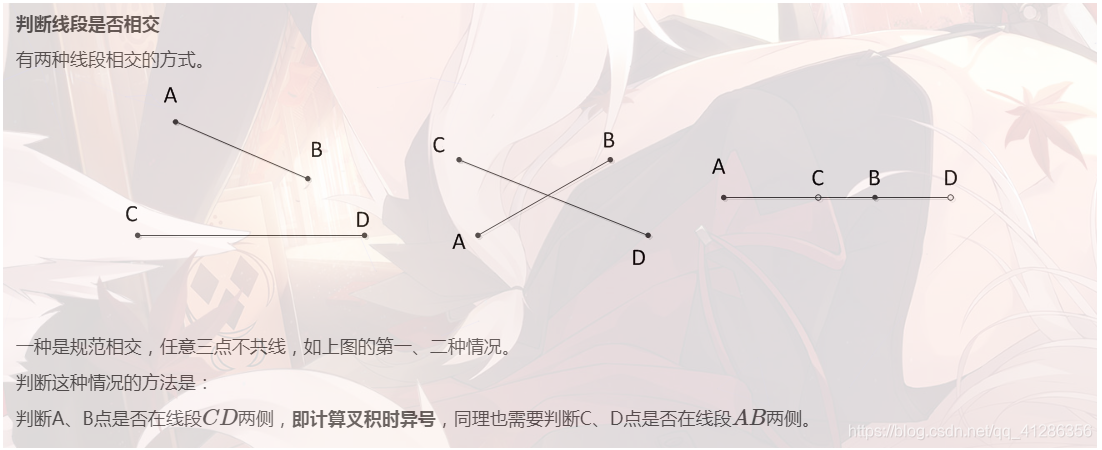
bool Segment_Intersection(Point a1,Point a2,Point b1,Point b2) {return dcmp(Cross(a2-a1,b1-a1))*dcmp(Cross(a2-a1,b2-a1))<0&&dcmp(Cross(b2-b1,a1-b1))*dcmp(Cross(b2-b1,a2-b1))<0;}

然后考虑第三种情况，也就是非规范相交，有至少三点共线。这情况发生时有一个点在其它线段上，判断一下即可。

bool _Segment_Intersection(Point a1,Point a2,Point b1,Point b2) {return Segment_Intersection(a1,a2,b1,b2)||OnSegment(a1,a2,b1)||OnSegment(a1,a2,b2)||OnSegment(a1,b1,b2)||OnSegment(a2,b1,b2);}

5、计算直线交点

Point GetLineIntersection(Point P,Vector v,Point Q,Vector w) {return P+v*(Cross(P-Q,w)/Cross(v,w));}

6、点到直线距离

叉积除以长度即可得到高度。

double DistanceToLine(Point p,Point a,Point b) {Vector v1=b-a,v2=p-a;return fabs(Cross(v1,v2))/v1.length();}

7、点到线段距离

判断下点是否在两个端点的中间，是则是垂直线，否则就是距离端点的距离才是点到线段的距离

double DistanceToSegment(Point p,Point a,Point b) {
    if(a==b)return (p-a).length();
    Vector v1=b-a,v2=p-a,v3=p-b;
    if(dcmp(Dot(v1,v2))<0)return v2.length();
    else if(dcmp(Dot(v1,v3))>0)return v3.length();
    else return DistanceToLine(p,a,b);
}

8、多边形面积、叉乘计算面积

#include<bits/stdc++.h>
using namespace std;
const int N=30;
struct Point{
   double x,y;
}p[N];
 
int n;
double polygonarea()
{
    int i,j;
    double area = 0;
    for(i = 0;i < n;++i){
        j = (i+1)%n;
        area += p[i].x*p[j].y;
        area -= p[i].y*p[j].x;
    }
    area /= 2.0;
    return area;
}

python写法：

class point:
    def __init__(self, x1, y1):
       self.x = x1
       self.y = y1

p = []
n = 0

def run():
    global n
    ans = 0
    for i in range(n):
        j = (i+1)%n
        print(i, " ", j)
        ans += p[i].x*p[j].y
        ans -= p[i].y*p[j].x
    return ans/2


n = int(input())
for i in range(n):
    x, y = map(int, input().split())
    a = point(x, y)
    p.append(a)

print(run())