《Grokking DRL》笔记(Chapter 8-10)
第8-10章重点讲解了基于值的RL算法。

Chapter 8
本书依然聚焦于强化学习问题中智能体与环境交互之后得到的feedback signal的形式,前7章包含了sequential and evaluative feedback,而DRL的目标是构建一个能够从sequential, evaluative and sampled feedback中学习的智能体. 深度强化学习是关于complex sequential decision-making problems under uncertainty的,其中complex对应着sampled feedback,sequential decision making对应sequential feedback, problems under uncertainty对应着evaluative feedback.

基础知识回顾
DRL智能体处理sequential feedback:
这类反馈信号的特点对应的问题就是temporal credit assignment问题,即动作的影响是有延迟的。
例子如下:

与其对立的一种情况是immediate feedback, or one-shot feedback. 对应的问题类型有supervised learning(例如分类问题), multi-armed bandits。 在图像分类问题中,下一批要被分类的图片不会因为上一批输入给模型的图片是否被正确分类而变化。在bandit问题中也没有遇到sequential feedback。但在DRL中,这些问题存在(数据和模型之间是存在相关性的)。


DRL智能体处理evaluative feedback:
evaluative feedback的问题在于智能体在交互过程中得到的feedback是relative的,因为环境是不确定的,智能体也不知道真实的environment dynamics (transition function and reward function)。对应的问题是exploration-exploitation trade-off。

evaluative feedback对立的是supervised feedback. 仍然以classification problem为例。

Bandit problem要从evaluative feedback中学习(chapter 4给出了该问题下的探索-利用平衡)。 该问题缺少supervision

DRL智能体处理sampled feedback:
DRL与tabular RL的区别在于问题的复杂度。DRL中智能体不可能exhaustively采样所有feedback,智能体需要有泛化能力,并基于此收集反馈并做出智能决策。
Supervised learning的核心问题处理sampled feedback,并能够泛化到新的样本。
sampled feedback的对立面是exhaustive feedback。tabular RL中面对的是exhaustive feedback,智能体只需要足够长的时间就可以采集所有的信息,因此Optimal convergence是存在的。

DRL解决的问题就是高维动作空间或状态空间。
Function Approximation for RL
使用函数近似的motivation是什么?强化学习问题可能会遇到高维状态或动作空间(例如Atari game中的pixel数量为210*160*3, 每一个像素的值有256个),或是连续的状态或动作空间(每一个状态的值都可以是无穷多个)。
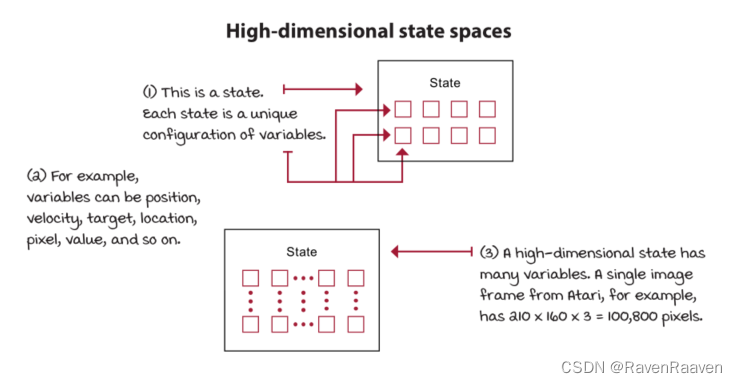

本章所使用的环境:CartPole

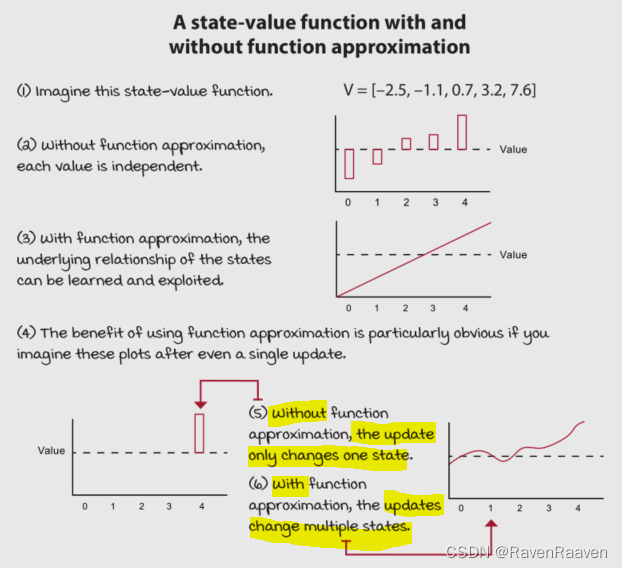
使用function approximation的优势:能够使算法变得更有效,泛化能力相比表格式RL更强,并且能够发掘更复杂的关系,在function approximation的帮助下,智能体可以借助更少的数据学习和利用模式。Q-learning这些基于表格式的强化学习算法缺少泛化的能力。例如要拟合的是state-value function,那么在使用function approximation进行更新的时候,不仅仅是更新某个状态所对应的状态值,而是更新更多状态对应的值,如下图:
Neural Fitted Q(NFQ)Iteration 算法的7个元素以及该算法存在的问题
value-based 算法的七个要素(也可以特指NFQ算法的七个元素):
-
选择要估计哪种值函数:状态值函数不能单独解决control problem,需要MDP的帮助(即引入决策)。第二种方法是估算action value function,该值可以解决control problem. 第三种是action-advantage function a(s,a)。本书大部分时候使用的是对action value function进行近似,记为 Q ( s , a ; θ ) Q(s,a;\theta) Q(s,a;θ)
-
选取神经网络架构:第一种是将状态和动作作为神经网络的输入,但这种方法比较低效,更高效的方式是将状态作为神经网络的输入,一次性输出所有动作对应的Q值

-
选择要优化的对象:最理想情况下的优化目标是最优Q值与估计得到的Q值之间的差值平方和,但是该目标是无法获取的,因为optimal policy是未知的,所以算法会在Policy evaluation(通过从中采样actions)和policy improvement(使用探索策略)之间迭代,直到找到更好的策略。


-
选择targets for policy evaluation, 有以下几种targets可以选择,MC target,TD target, n-step target, lambda target. TD target中又分为SARSA target和Q-learning target。

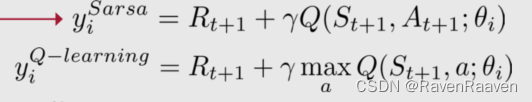
将第三步中的optimal action-value function替换为TD target.

实现的过程中需要注意两个问题:第一个问题是只对Predicted values进行反向传播。RL中所谓的true values也来自Learned model (bootstrapping),上文中的targets中的第一项reward是常数,但第二项是由model计算得出的, 会导致一系列问题。在实现的时候将targets都设置为常数,在Pytorch中要使用detach method。第二个问题是如何处理terminal states. openAI GYM环境会手动终止环境条件,防止智能体花费太多timesteps完成一个任务。但问题在于如果规定范围内最后一个Timestep的本应该是获取奖赏值的state-action pair,由于该状态被人为设置为了结束,那么值函数就无法基于此更新。对于OpenAI gym可以找到“TimeLimit.truncated” in the info dictionary
-
选择探索策略。注意On-policy和off-policy的区别。
-
选择损失函数。MSE (mean squared error, or L2 loss),损失函数中的true values是TD targets, 而Predicted values是action-value function.
- 选择一个优化方法。机器学习中常用的优化算法是gradient desecnt,如果要其稳定的话,需要以下几个假设:数据IID (independent and identically distributed),targets必须是stationary. DL中较为流行的一个方法有以下几种:

其局限性在于batch gradient descent每次使用整个数据集。第二种方法式mini-batch gradient descent。

mini-batch gradient descent,一次只用一部分数据。如果将Mini-batch的batch-size设置为1,即得到了stochastic gradient descent. mini-batch size的大小一般在32~1024之间。

momentum方法朝着gradients的moving average更新网络参数,而不是gradient本身。momentum的代替算法是root mean square propagation (RMSprop)。

RMSprop采用更平稳的方法,按梯度幅度的移动平均值按比例缩放梯度。(RMSprop takes the safer bet of scaling the gradient in proportion to a moving average of the magnitude of gradients. 更准确的是 square root of the moving average of the square of the gradients均方根)
另一种方法Adam is a combination of RMSprop and momentum。Adam比RMSprop更激进。
RMSprop相比于Adam在基于值的方法中更稳定,对超参数不敏感。
完整的NFQ算法:

NFQ算法的问题:
第一个问题在于神经网络会一次性更新所有相似状态的值函数。因此所使用的targets是不稳定的。(non-stationary targets),因此训练也变得不稳定。

第二个问题在于使用的mini-batch数据相互之间是Correlated,因为大部分数据是来自于同一个trajectory和策略。这就意味着深度强化学习问题中IID假设是不成立的,与优化算法的假设相违背。下一个状态depend on the current state. 而策略的分布也是不断变化的,导致样本不是identically distributed。

Chapter 9
NFQ解决上述两个问题(非IID分布和Non-stationary targets)的思路是使用mini-batching and trianing one mini-batch for multiple epochs.
但也存在更好的解决技术。
Non-stationarity的问题:

DQN算法
- 使用target networks:目的是让targets的值更加稳定。用一个单独的网络计算targets.
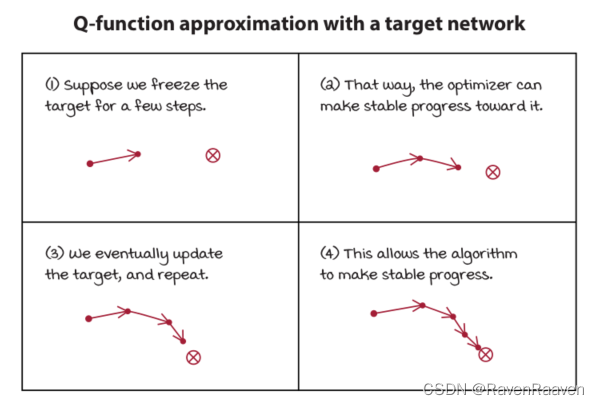

target network的参数更新频率取决于要解决的问题,例如如果使用卷积神经网络解决Atari games, 则网络的尺寸选为10000为标准。使用target network的缺点在于我们放慢了Learning的速度。

- 使用更大规模的网络. 使用规模更大的网路的优势在于不同states之间的微小差异可以被检测出来。这一方法可以减少consecutive samples之间的相关性。

- 使用experience replay:解决的是数据不符合IID分布的问题,从buffer中采样更像深度学习中的supervised learning。

- 使用其他的探索策略:decaying epsilon-greedy, softmax strategy.
整个DQN的算法框图和总结:

Double DQN
DQN存在的问题是:overestimation,存在问题的原因在于DQN的targets中采用了Max运算符。
相比于DQN所做的改进措施:将action selection和action evaluation分开。在具体实现中,首先是将max进行unwrapping,max的过程就是先进行argmax, 之后利用argmax获取得到的动作对Q值进行选择,最后等效得到argmax.

如果直接将chapter 6中的double Q learning扩展到function approximation会带来不必要的内存负担(overhead),训练需要两个网络,还有其分别对应的target networks,总共4个网络。一个更符合实际的解决方案是:直接将target network作为第二个网络,训练只训练一个Online model,而不训练target network, 类似于监督学习中的交叉验证。具体顺序是让Online model选择best action, 再让target network评估动作的好坏。


对于损失函数的选择:不仅仅可以选择MSE,也可以选择其他损失函数,MSE的缺点在于其相对于small errors,它惩罚large errors. 解决这个问题的另外一种奖赏函数是L1 loss (mean absolute error)。但MAE不足的地方在于梯度不会随着Loss趋于0而减少,因为梯度的减少说明函数值越来越接近最优解。Huber loss是这两个函数的混合。该函数由二次型函数和线性函数组成,在阈值范围(threshold δ \delta δ)之上是线性函数,在临近0附近是二次函数。损失函数、优化方式、学习率之间都是相互影响的。huber loss的实现方式包括两种,一种是直接对该函数的表达式进行实现,第二种是选择MSE作为损失函数,并对超过某个阈值的梯度设置为固定值,即clip the magnitude of the gradients.
Chapter 10
本章的目的是为了提升DQN算法的sample efficiency, 第一种方法是dueling DDQN, 将Q function切换成两个stream, 第一个近似计算V-function, 第二个近似计算A-function. 第二种方法是prioritizing replay。
Dueling DDQN
dueling netwrok architecture是加在网络结构上的改进。

Dueling DQN提出的motivation: 非dueling结构每次只能更新一个action. dueling结构每次都能够更新对于actions来说是全局的信息 V ( s ) V(s) V(s),该信息对于所有状态都是可获取的,因此更新效率会更高。
使用advantages的优势:advantage function可以捕获动作的‘favorability’,可以轻易地看出动作值的大小并判断做出什么样的动作。
在构建网络结构的时候,对于 V ( s ) V(s) V(s)和 A ( s , a ) A(s,a) A(s,a),在输出层的前一层要共享网络层和参数。如下图所示:


如何reconstruct the action-value function? 由于给定V,A不能重构出唯一的Q值,并且Advantage需要满足期望值为0的约束条件,所以在重建Q值的时候需要减去一个A的平均值。这样做的好处是可以稳定优化过程。


接下来是target network参数更新的问题,问题之一是使用的数据都是旧(stale)的,这些数据可能对网络的训练没有益处。问题之二是每隔一段时间都要对网络做一次很大的更新。这些问题都会造成训练的不稳定。
解决办法之一是Polyak Averaing, 每一步都保留大部分的网络参数,并对一小部分网络参数进行更新。
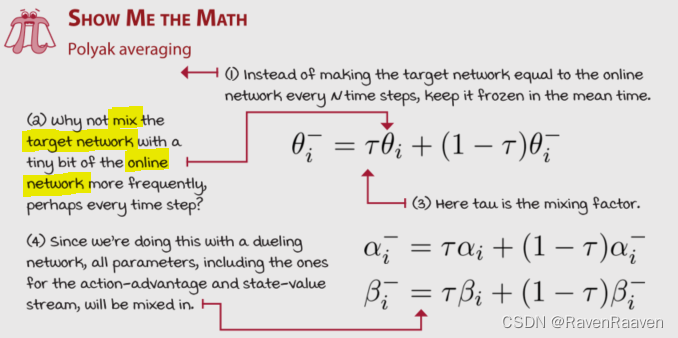

Dueling network的优势:能够快速并准确地对比值相近的动作,并且减少了function error and error variance,提升了policy evaluation的准确度。
如何直观理解哪一个算法更擅长对similarly valued action进行分辨?更好的算法得到的range更小,状态值的分布在中心范围附近。
Dueling DDQN相比于DDQN更加的sample efficient。
PER: Prioritizing the replay of meaningful experiences
一个反直觉的事实:一味地从replay buffer中给智能体more rewarding experiences并不能让智能体变得更好,反而会适得其反。在训练的过程中也是需要负样本的。那么该如何定义什么是‘重要的’样本呢?
直觉上应该是哪些能够让人‘意外的’样本,即期望和真实值(expectation and reality)相差较大的样本。强化学习中衡量该值的是absolute TD error。
选择TD error的优势在于计算方式已经给定了,而其他方法例如每一步计算replay buffer中数据的梯度是不现实的。

只使用Greedy prioritization by TD error会给算法带来哪些问题(即只根据TD error的大小来判断对应样本的重要程度会带来哪些问题)?
TD error计算了两次,第一次在将其加入replay buffer中,第二次在用TD error对网络进行训练的时候;解决方法是只更新用于训练网络的experiences的TD errors,并将其存入buffer并按照值的大小进行排序。但是又会出现其他问题,为0的TD error的数据不会被采样获取。第二,由于使用的是神经网络近似,损失会下降地非常快,说明更新只会发生在buffer中的一小部分中。除此之外,TD errors包含噪声,如果只是贪婪地采样,结果会严重被这些噪声所影响。

采样随机方式基于TD errors对replay buffer进行采样。为什么需要stochastic prioritization?随机场景和神经网络的使用都会造成TD errors方差较大。
思路就是先利用TD errors计算Priorities,再通过Priorities进行sample probability。
有以下2种根据TD errors对样本进行采样的方式:
- **Proportional prioritization:**加入epsilon的目的是保证0 TD errors的样本也有几率被采样到。之后根据该值进行类似softmax的计算。


当 α \alpha α为0 时,采样的方式就是均匀采样,当 α = 1 \alpha=1 α=1的时候,就是greedy prioritization.
- Rank-based prioritization:proportional prioritization方法的缺点在于对outliers敏感,即较大TD error对应的样本(可能受噪声的影响)会有更大概率被采样。一种解决方法是通过rank来采样样本。rank指的是通过按TD error降序排列后所对应样本的位置(the position of the sample when sorted in descending order by the absolute TD error,for instance, highest absolute TD error rank 1, the second rank 2)。priority为rank的倒数,之后继续对priorities进行类softmax处理。


Prioritization bias
bias的问题出现在:使用一个分布去估算另一个分布会带来estimate bias. 我们的采样是基于通过priorities计算得来的概率分布,因此用这些从上述概率分布采样出来的数据进行更新与之前的公式中(之前的公式中数据的采样满足均匀分布 U \mathcal{U} U)期望的分布相同。下面的公式为之前的DDQN的损失函数公式。其中期望的分布是均匀分布。

更新的过程中使用到了reward,reward是均匀从replay buffer中采样获得的,而prioritization的问题在于它并不是均匀分布。
解决办法:利用重要度采样weighted importance sampling,目的是修改updates的大小,使其类似于均匀分布。
这里的期望遵循的分布是
U
(
⋅
)
\mathcal{U}(\cdot)
U(⋅),而prioritization的分布是
P
(
⋅
)
P(\cdot)
P(⋅)。重要性采样的公式是:
E
x
∼
U
[
f
(
x
)
]
=
E
x
∼
P
[
U
P
f
(
x
)
]
E_{x\sim \mathcal{U}}[f(x)]=E_{x\sim P}[\frac{\mathcal{U}}{P}f(x)]
Ex∼U[f(x)]=Ex∼P[PUf(x)],公式如下

这里的weight为:
U
/
P
\mathcal{U}/P
U/P,可以理解为:
w
i
=
(
N
P
(
i
)
)
−
β
=
(
1
N
)
β
P
(
i
)
β
w_i=(NP(i))^{-\beta}=\frac{(\frac{1}{N})^{\beta}}{P(i)^{\beta}}
wi=(NP(i))−β=P(i)β(N1)β
这里的超参数
β
\beta
β只是为了更好地调参,从而更好地优化算法效果。 当该值为0,则完全没有weighted importance sampling,这时bias最大;如果该值为1,则对于的是full correction of the bias。

这里期望的分布遵从prioritized sampling distribution,因此相比于原先的公式(DDQN的损失函数公式是按照均匀分布来计算的),需要在期望内的函数中增加一个权重项,权重见上述公式。








 本文深入探讨了深度强化学习(DRL)中的价值函数近似,包括状态值函数、动作值函数和优势函数。介绍了DQN算法及其改进,如双Q学习、经验回放缓冲区、目标网络和 Dueling DQN,以解决非平稳目标和样本效率问题。此外,还讨论了优先重播策略以增强样本选择的重要性,并分析了损失函数、优化方法和探索策略对算法性能的影响。
本文深入探讨了深度强化学习(DRL)中的价值函数近似,包括状态值函数、动作值函数和优势函数。介绍了DQN算法及其改进,如双Q学习、经验回放缓冲区、目标网络和 Dueling DQN,以解决非平稳目标和样本效率问题。此外,还讨论了优先重播策略以增强样本选择的重要性,并分析了损失函数、优化方法和探索策略对算法性能的影响。
















 3995
3995

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








