二十七、 影子价格（对偶问题）

原文视频：https://www.bilibili.com/video/BV194411y7sA?p=27&spm_id_from=pageDriver

 

对偶问题（数学模型）中的经济意义

  最优目标为最大值（利润最大）

例1、（杜刚教授）某工厂可生产甲、乙两种产品，消耗 煤、电、油三种资源，相关数据如下，求总收入最大的生产计划方案        P问题（原问题）

	甲	乙	资源限制
煤	9	4	360
电	4	5	200
油	3	10	300
单位产品价格	7	12

 

 

 

 

 

 

                   

     

 

（1）对偶问题最优解的经济意义（影子价格）

         其他方法：

            

          （上一节，性质六：原问题终表的松弛变量检验数的负值，就是对偶问题的最优解）

       本方法：

             资源的影子价格   ：    数学上的表示 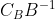  （对偶问题的最优解）（在原问题的终表上，能够直接看出）

         （1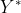）   （shadow price） ：买主的最低出价

         （2）  原问题的影子价格： 当对应资源的限制（其他资源不变），每增加一个单位时，引起的卖方总收入的增加（卖家的内控价格）

 

 注：

（1）影子价格反映资源对目标函数的边际贡献，即资源转换成经济效率的效率

（2）影子价格反映了资源的稀缺程度

                  影子价格 = 0 表示资源 有剩余

                  影子价格 > 0 表示资源 用尽了，且越大的数，代表价值转换率越高，更应该关注

（3）反映了资源的边际使用价值