旅行商问题、约束重构建

 

旅行商问题（The Traveling Salesman Problem (TSP)）

（1）给定一个无向图，以及对应每个边（edge）对应的成本（cost），目标函数是找到一个最小成本的回环（tour，遍历所有点）

（2）对于边定义一个变量，如果e边包含在回环中为“1”，否则为“0”

（3）旅行商问题可以描述为如下：

                                       最小化回环的总成本

                     对于任意节点，只有两条边出现在回路中（一进一出）

                                     只使用上一个约束，容易使两点之间产生子环，而不能生成连续的整条路径，因此对于S集合中的点，至少要与外界存在两个或两个以上的边才能保证这个集合不是孤立的。

其中是的割集，（对于边的两个端点来说，一个端点在S内，另一个不在），则表示与节点i相关的所有边

（4） 约束（*）表示的是子回环的消除（elimination）约束，并且其数量为指数个

 

带有容量的车辆路径问题（The Capacitated Vehicle Routing Problem (CVRP) ）

（1）给定一个无向图：

         （a）是n+1个节点

         （b） 节点0 代表仓库（depot），而 表示n个顾客（consumer）

         （c）  对于每条边都有一个非负的成本

         （d）每个顾客都需要从仓库提供个单位的需求

         （e）个容量为的相同车辆，停放在仓库0

（2）如果整个路径由一个穿过仓库0的相图G中的一个普通回环构成，这样定义的话顾客的总需求量不能超过车辆容量

（3）路径的总成本，与形成路径的边的总成本相关

（4）目标：设计个路径，每一个对应一个车辆，这样所有的顾客都将仅被访问一次，并且总和的路径成本是最小的

               

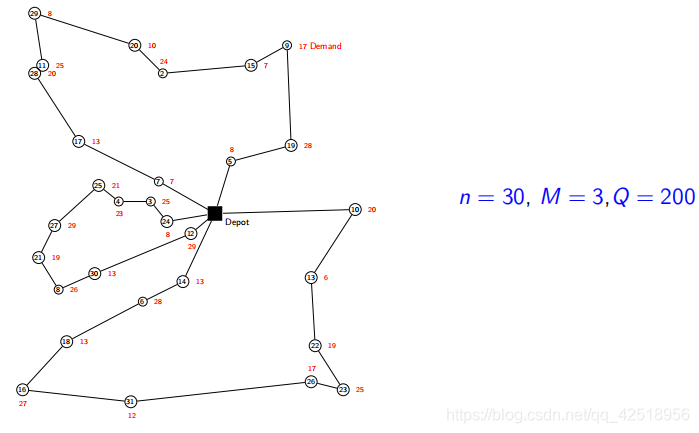
集合划分模型

（1）令为所有可行路径（feasible routes ）的索引集合（index set）

（2）令为一个（0/1）的一个相关系数，当且仅当 点，包含在路径时，取值为“1”

（3）每个路径都包含相对应的成本

（4）令为一个二进制变量，当且仅当在最终结果中时，取值为“1”

（5）集合划分模型（set partitioning formulation）

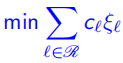                                 在所有可行路径中，找到最小成本的集合

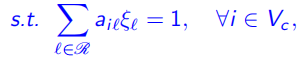               对于所有顾客节点，只包含在一条最终选用的路径中

                               选用的路径总数，等于车辆总数

                     

 

整数规划的几何模型

（1）在此考虑整数线性规划问题  Integer Linear Program (ILP):

                             

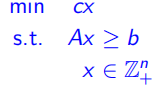
（2）整数约束使得可行区域只包含于多面体相关的整数坐标系上的点，如果移除整数约束，那么LP将提供一个分数结果

（3）最优LP解为ILP最优解提供一个最低界（lower bound）       

         （由于线性规划可行区域 大于 整数线性规划可行域， 因此线性规划的最优解 一定要不大于 整数线性规划最优解）

（4）如果LP解为整数解，那么也就是ILP的最优解

                

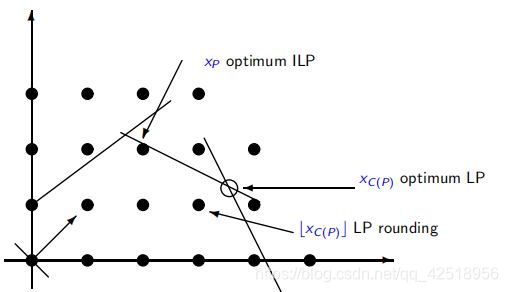
（1）一般情况，LP松弛问题的最优解不能用来确定ILP问题的最优解的信息（可能会离LP最优解很远）

（2） 近似出一个可行整数解很困难：

                       （a） 近似可能造成结果远离最优解

                       （b）可能会取到不可行解

 

重新约束（Reformulation）

（1）Reformulation（换一种问题描述方法）用来得到强线性松弛（stronger LP relaxations），从而在确切算法中使用较好的对偶边界（dual bounds）

（2） 得到reformulation的方法：

            （a） 添加有效不等式（valid inequalities ）（割平面，cutting planes）

            （b）使用问题结构（problem structure）

            （c）添加新变量（new variables），源自扩展约束（derive extended formulations）

（3）求解整数规划的目标：

          

          其中，，

         对于混合整数规划问题（Mixed Integer Program (MIP)）：

           

         其中，，

 

多面体，约束、理想约束（Polyhedra, Formulation and Ideal Formulation ）

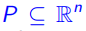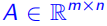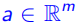定义1：一个多面体是有限个半平面的交集，也就是存在和满足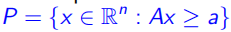

定义2：如果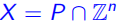，那么多面体P是X的一个约束（formulation）

     如果是对于的两个约束，并且，那么称约束比约束更强，因为，

                          

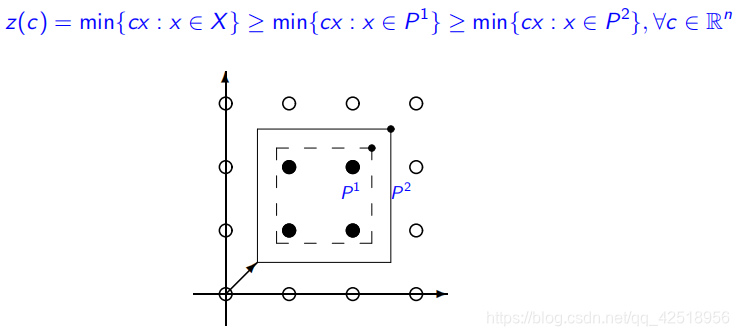
            可行域范围更小，能够取的值更少，约束更强！

定义3：给定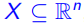，X的凸包（convex hull）记做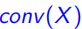，它是包含X的最小封闭凸集（smallest closed convex set）

                              

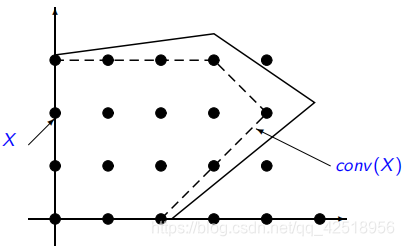
Proposition 1. 整数集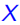（或一个混合整数集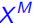）的凸包是一个多面体

（1）因此，最有可能或最理想的约束，是由决定的：

                 

（2）实际上，需要由指数个不等式来描述，并且它们无法被简单表达

 

拓展约束

定义4：给定一个集合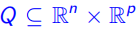，前 n 个变量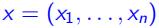的投影为集合：

              

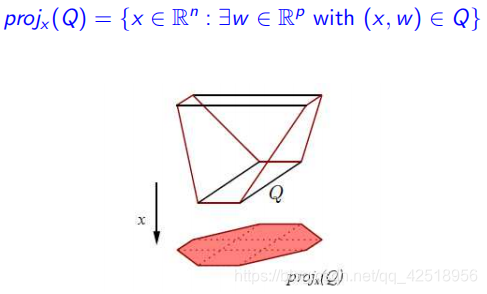
定义5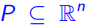：的一个拓展约束是一个多面体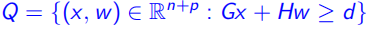，其中

 

无容量批量规划问题（Uncapacitated Lot-Sizing Problem (ULSP)）（以时间点作为约束）

（1）此问题决定生产计划中对于单个产品的 n 个时间段（period horizon）：

              （a）  是时刻的固定生产成本（fifixed cost）

              （b）是时刻的单位生产成本（unit production cost）

              （c）是时刻的单位存储成本（unit storage cost）

              （d）是时刻的需求量（demand）

（2） 使用的变量：

              （a）是的生产数量

              （b）是结束时的存储量

              （c）如果进行了生产，那么，否则

      

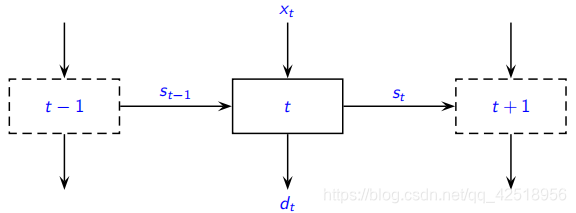
（1）定义（初始库存为0，最终会卖掉所有库存也为0），并且令是一个非常大的值

（2）约束如下：

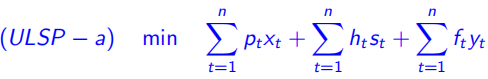                          固定生产成本+生产成本+存储成本  的最小化

                             对于任意时刻，前一时刻的库存 + 当前时刻生产量 = 需求量（消耗量）+ 当前时刻库存 

                                            控制是否进行生产

                              

 

拓展约束（以过程作为约束）

（1）假设，将时间段分解为为更小的区间

（2）定义变量，作为在时间段的生产量并且满足到t时刻的需求

（3）现在， （时间段i之后的所有需求），约束条件可以变为如下：

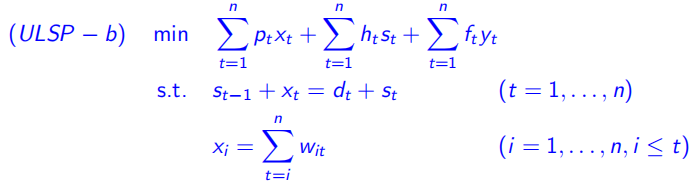                                   从i 时刻，一直到最终的n时刻的总和

                                                            约束每个不超过当前t时刻的需求量

                                                   

 

（1）考虑LP松弛问题的两种约束

（2）分别表示两种约束方法的结果

（3）令

（4）：对于所有t时刻，点是的极点，而不是的，

（5）因此，能够给出比更好的下界

（6）描述的是问题解的凸包，因此是个理想的约束