VINS-Mono中的边缘化与滑窗 (4)——VINS边缘化为何是局部变量边缘化？

VINS-Mono代码注释：https://github.com/Cc19245/VINS-Mono-CC_Comments

0.前言

题目想问的问题是VINS 滑窗边缘化时构造舒尔补的H矩阵是由和边缘化掉的状态变量相关的局部变量构成还是由全局变量构成？

1.系统构建

1.1.仿真模型

如下图所示，小车沿着一维方向运动，车上有一个单点激光测距仪可以观测前方的一个路牌，小车轮子上装有码盘。现在让小车从原点出发，维持滑窗的长度为3，并且每次优化都迭代3次。

1.2.第一次滑窗优化

定义此时系统估计的状态变量为$(P_0,P_1,P_2,L)$，其中3个坐标位置和滑窗有关，会随着滑窗的滑动逐渐改变。则此时系统中的各个残差和雅克比如下：
$$\begin{gathered} r_0=6.0-(L-P_0) \\ {J}_0=[1,0,0,-1] \end{gathered}$$

$$\begin{gathered} r_1=1.1-(P_1-P_0) \\ {J}_1=[1,-1,0,0] \end{gathered}$$

$$\begin{gathered} r_2=0.95-(P_2-P_1) \\ {J}_2=[0,1,-1,0] \end{gathered}$$

$$\begin{gathered} r_3=5.05-(L-P_1) \\ {J}_3=[0,1,0,-1] \end{gathered}$$

$$\begin{gathered} r_4=3.8-(L-P_2) \\ {J}_4=[0,0,1,-1] \end{gathered}$$

所以总的雅克比矩阵$J$和残差$r$如下，这是一个线性模型，所以SLAM中的FEJ问题就不存在了。
$$\begin{gathered} r=\left[\begin{array}{c}6.0-(L-P_0)\\ 1.1-(P_1-P_0)\\ 0.95-(P_2-P_1)\\ 5.05-(L-P_1)\\ 3.8-(L-P_2)\end{array}\right] \\ J=\left[\begin{array}{cccc}1& 0& 0& -1\\ 1& -1& 0& 0\\ 0& 1& -1& 0\\ 0& 1& 0& -1\\ 0& 0& 1& -1\end{array}\right] \end{gathered}$$

现在进行优化，线性模型仍然可以使用非线性优化的方式来求解。现在设置初始状态即各个状态的初始值就是码盘估计的值，那么求解代码如下：

clear all; clc;

%% 1.正常状态，滑窗中维护3个位置+1个路标点
disp("----------1.正常状态，滑窗中维护3个位置+1个路标点--------------");
% 真实状态
x_t = [0; 1; 2; 6];  % 滑窗长度为3, 变量分别为P0, P1, P2, L
% 码盘测量值, e=encoder, l=lidar
l0 = 6; e1 = 1.1; e2 = 0.95; l1 = 5.05; l2 = 3.8;
% 状态初值, 由码盘测量值来得到
P0 = 0; P1 = P0 + e1; P2 = P1 + e2; L = P0 + l0; 
% 状态初始估计值
x = [P0; P1; P2; L]; 

% 雅克比矩阵保持不变, 因为是线性模型
J = [1, 0, 0, -1;
     1, -1, 0, 0; 
     0, 1, -1, 0;
     0, 1, 0, -1;
     0, 0, 1, -1];

% 开始构造高斯牛顿的优化问题，认为信息权重矩阵都是I
H = J' * J;
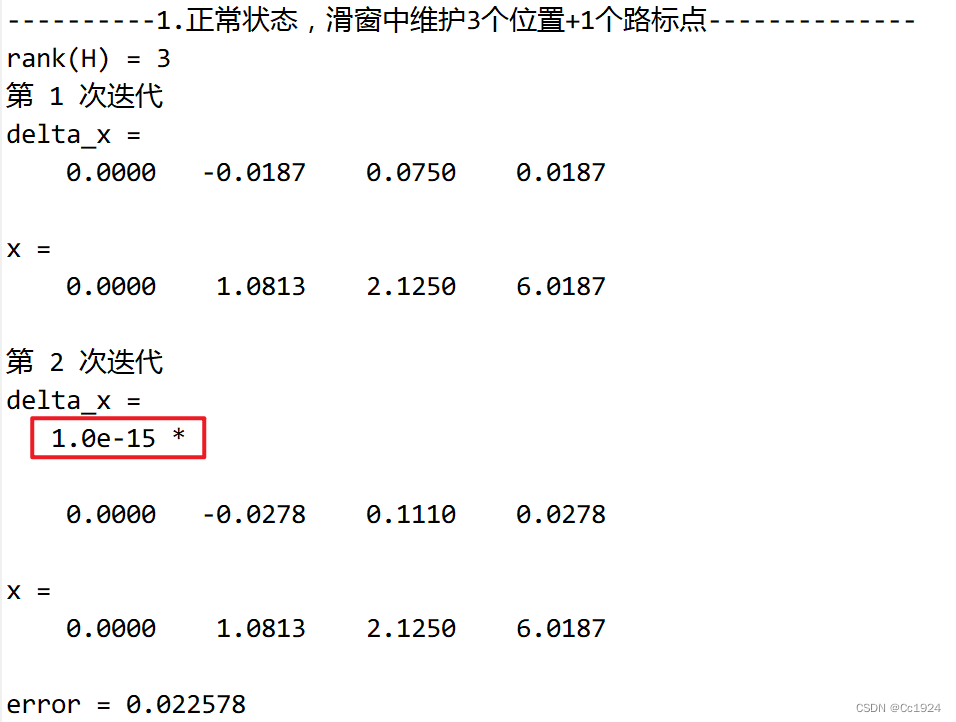
fprintf("rank(H) = %d\n", rank(H));  % rank(H) = 3
% x = H\b;  % 警告: 矩阵为奇异工作精度
% 由于H奇异，无法求解。所以按照g2o中的方式, 把第0帧位姿固定，即H中第0帧位置+I
H(1, 1) = H(1, 1) + 1; 
% H = H + eye(4); % 这里测试使用LM算法求解
% 其实由于是线性模型，所以没必要迭代，一步就是最速下降法得到最优解
% 这里故意迭代两次就是看看第2次迭代是不是步长已经很小来判断第1次是否收敛
for i = 1 : 2
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r = [l0 - (x(4) - x(1));
         e1 - (x(2) - x(1)); 
         e2 - (x(3) - x(2));
         l1 - (x(4) - x(2));
         l2 - (x(4) - x(3))];
    b = -J' * r;
    delta_x = H \ b;
    x = x + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x = "); disp(x');
end
fprintf("error = %f\n", (x_t-x)' * (x_t-x));

代码输出如下：

上述代码中，有几个细节问题需要注意：

• 很明显这个系统是1自由度不可观的，因为不论是码盘的测量值还是激光的测量值都是测量相对位置，而没有像GPS一样的绝对位置测量。因此如果把所有估计的状态都进行一个偏置，那么这些测量值和系统状态构成的残差仍然不改变，所以优化过程中系统会在零空间里面漂移。从上面的代码操作也可以看出来，如果直接求解H矩阵的话，估计的状态是4维的，也就是H矩阵是4x4的，但是H矩阵秩为3，即存在一个1维的零空间。这样直接用MATLAB的KaTeX parse error: Undefined control sequence: \b at position 2: H\̲b̲求解是不能求解的。

  为了固定住这个1维的零空间，这里使用了g2o中的方式，在H矩阵的第0帧的位置上，也就是H(1,1)的位置（MATLAB索引从1开始）加上单位阵，从而优化的时候会固定住第0帧不优化。从代码输出结果也可以发现，由于是线性模型，并且固定住了第0帧，结果经过一次迭代就达到了最优值。

• 另外在SLAM的非线性优化方式中，经常会使用LM求解的算法，LM会在H矩阵上增加$\mu I$这一项当做置信域，这样会间接地改变H矩阵的秩，让它变成满秩的，但是注意求解结果仍然会在零空间进行漂移。代码输出如下所示，可以发现，经过8次迭代的话，求解的时候更新量仍然在$10^{-4}$的数量级，而用上面g2o固定第0帧的方式，直接一步到位。所以后面可以考虑一下在VINS中如何添加优化时的四自由度固定？

1.3.第二次全局优化

当到来下一个状态$P3$的时候，也就是系统的仿真模型变成如下形式，这个时候不使用滑窗的方式，仍然进行全局的优化。这样是为了和后面不同的边缘化构建H矩阵的方式进行对比，看后面两种不同的操作哪种更接近全局优化的方式。

定义此时系统估计的状态变量为$(P_0,P_1,P_2,P_3,L)$，那么此时系统的残差矩阵和雅克比矩阵变成如下形式：
$$\begin{gathered} r=\left[\begin{array}{c}r0=l0-(L-P0)\\ r1=e1-(P1-P0)\\ r2=e2-(P2-P1)\\ r3=e3-(P3-P2)\\ r4=l1-(L-P1)\\ r5=l2-(L-P2)\\ r6=l3-(L-P3)\end{array}\right]=\left[\begin{array}{c}6.0-(L-P_0)\\ 1.1-(P_1-P_0)\\ 0.95-(P_2-P_1)\\ 1.05-(P_3-P_2)\\ 5.05-(L-P_1)\\ 3.8-(L-P_2)\\ 3.05-(L-P_3)\end{array}\right] \\ J=\left[\begin{array}{ccccc}1& 0& 0& 0& -1\\ 1& -1& 0& 0& 0\\ 0& 1& -1& 0& 0\\ 0& 0& 1& -1& 0\\ 0& 1& 0& 0& -1\\ 0& 0& 1& 0& -1\\ 0& 0& 0& 1& -1\end{array}\right] \end{gathered}$$
那么此时再次进行全局优化，仍然固定第0帧，代码如下：

%% 2.再来一个状态，如果不进行滑窗，此时进行优化的结果是最准确的
disp("------2.再来一个状态，如果不进行滑窗，此时进行优化的结果是最准确的---------");
% 真实状态
x_t3 = [0; 1; 2; 3; 6];  % 状态变量变成4个，分别为P0, P1, P2, P3, L
% 这一次的测量
e3 = 1.05; l3 = 3.05; P3 = P2 + e3; 
% 初始状态估计，仍然是由码盘测量得到
x3 = [P0; P1; P2; P3; L];
% 雅克比矩阵，7x5
J3 = [1, 0, 0, 0, -1;  % r0 = l0 - (L - P0)
      1, -1, 0, 0, 0;  % r1 = e1 - (P1 - P0)
      0, 1, -1, 0, 0;  % r2 = e2 - (P2 - P1)
      0, 0, 1, -1, 0;  % r3 = e3 - (P3 - P2)
      0, 1, 0, 0, -1;  % r4 = l1 - (L - P1)
      0, 0, 1, 0, -1;  % r5 = l2 - (L - P2)
      0, 0, 0, 1, -1]; % r6 = l3 - (L - P3)
H3 = J3' * J3;
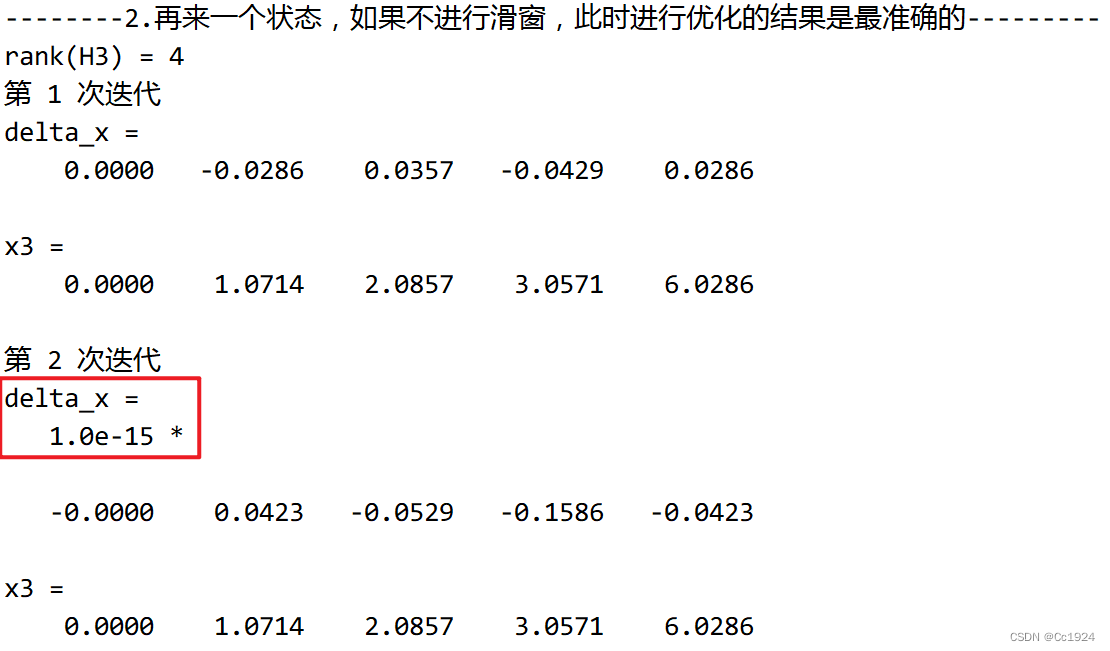
fprintf("rank(H3) = %d\n", rank(H3));  % rank(H) = 3
H3(1, 1) = H3(1, 1) + 1;  % 固定第0帧不优化

for i = 1 : 2
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r3 = [l0 - (x3(5) - x3(1));
          e1 - (x3(2) - x3(1)); 
          e2 - (x3(3) - x3(2));
          e3 - (x3(4) - x3(3));
          l1 - (x3(5) - x3(2));
          l2 - (x3(5) - x3(3));
          l3 - (x3(5) - x3(4));];
    b3 = -J3' * r3;
    delta_x = H3 \ b3;
    x3 = x3 + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x3 = "); disp(x3');
end

代码输出如下：

2.边缘化时不同的舒尔补方式

2.1.边缘化时舒尔补的意义

按照VIO课程中讲的（第四讲PPT25-26页），舒尔补时进行的边缘化，相当于从原来滑窗中的所有状态变量的联合分布$p(a,b)$求解边缘化留下的变量的边缘概率分布$p(a)$。并且PPT中的表格里对比了相应的求条件概率的情况。

疑问：为什么这里边缘化时求边缘概率分布，而不是求条件概率分布呢？此时变量$b$被边缘化掉，不就是相当于求解在$b$变量发生的条件下剩下的状态变量发生的概率吗？不就是条件概率分布吗？

这个地方还不是很理解，后面慢慢理解吧。

2.2.不同的边缘化方式

在VIO课程中讲解的舒尔补存在两个貌似矛盾的地方。

一个是如下的操作，对整个优化的因子图进行舒尔补，得到边缘化之后的矩阵。这种方式比较容易理解，就是在全局的整个H矩阵上进行舒尔补操作。

但是在后面讲解滑窗过程中操作的一个例子中，又说margin变量的信息与${\xi }_6$不相关。这种方式就是只在由${\xi }_1,{\xi }_2,{\xi }_3,{\xi }_4,{\xi }_5$构成的一个局部的H矩阵中进行舒尔补。

二者有什么区别呢？如果从概率的角度理解，第一种全局的方式比较好理解，就是在求一个边缘概率（或者可能是条件概率？）。但是第二种方式就不太好理解了，好像变成一个局部的边缘概率了？

如果从最小二乘的角度去理解的话，那么二者的意义就都很明显了。第一种全局的方式是考虑全局所有测量的残差，然后把和第0帧有关的测量残差分散到剩余其他的变量上。而第二种局部的方式，则是只考虑和第0帧有关的残差，由于这些残差都是相对测量量形成的，也就是都是第0帧位置和其他变量（第1帧位置，路标点位置）构成的，所以可以通过边缘化把这个残差全部转移到$P_1,L$上，而不是转移到其他所有的状态变量上。二者的不同可以按照如下面的图优化来理解，其中红色边是优化中考虑的边。

到底哪种方式是对的呢？一开始我认为应该是全局的舒尔补操作是对的，因为这样它考虑的是所有的误差。但是经过后面的实验发现，其实是第二种局部的schur操作是对的。

3.边缘化时不同的舒尔补方式实验验证

3.1.全局schur的操作方式

这种方式就是在本次滑窗优化之后，对全局的H矩阵进行舒尔补，然后再进行矩阵的分解得到舒尔补先验的残差和雅克比，并给下一次优化使用。代码如下：

%% schur方式1：对整个H矩阵进行schur补
disp("---schur方式1：对整个H矩阵进行schur补----");
H(1, 1) = H(1, 1) - 1;  % 回归到J' * J
% 首先更新一下最后一次优化之后的残差, 并重新计算B
r = [l0 - (x(4) - x(1));
     e1 - (x(2) - x(1)); 
     e2 - (x(3) - x(2));
     l1 - (x(4) - x(2));
     l2 - (x(4) - x(3))];
b = -J' * r;
s_H = H(2:end, 2:end) - H(2:end, 1) * H(1, 2:end) / H(1, 1); % 手动执行舒尔补
% disp("rank(s_H) = "); disp(rank(s_H));
s_b = b(2:end, 1) - H(2:end, 1) * b(1) / H(1, 1);
[V, D] = eig(s_H);   % A*V = V*D, 即 A = V*D*V'(V' = V^-1)
sqrt_D = sqrt(D)
% 这里求逆是根据sqrt_D结果手动写的
sqrt_D_inv = [0, 0, 0; 0, 1.0/sqrt_D(2,2), 0; 0, 0, 1.0/sqrt_D(3,3)];
s_J = sqrt_D * V';   
s_r = -sqrt_D_inv * V' * s_b;

%% 舒尔补方式1进行下一次滑窗优化
fprintf("舒尔补方式1进行下一次滑窗优化------------------------\n");

x1 = [x(2); x(3); x(3) + e3; x(4)];
J1 = [1, -1, 0, 0;
     0, 1, -1, 0;
     1, 0, 0, -1;
     0, 1, 0, -1;
     0, 0, 1, -1;
     s_J(1,1), s_J(1,2), 0, s_J(1,3);
     s_J(2,1), s_J(2,2), 0, s_J(2,3);
     s_J(3,1), s_J(3,2), 0, s_J(3,3)];
H1 = J1' * J1;
fprintf("rank(H1) = %d\n", rank(H1));  % rank(H1) = 3
H1(1, 1) = H1(1, 1) + 1; % 下一次的滑窗优化仍要固定滑窗中的第1帧
for i = 1 : 2
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r0 = s_J * ([x1(1); x1(2); x1(4)] - [x(2); x(3); x(4)]);
    r1 = [e2 - (x1(2) - x1(1));
         e3 - (x1(3) - x1(2));
         l1 - (x1(4) - x1(1));
         l2 - (x1(4) - x1(2));
         l3 - (x1(4) - x1(3));
         s_r(1) + r0(1);
         s_r(2) + r0(2);
         s_r(3) + r0(3)];
    b1 = -J1' * r1;
    delta_x = H1 \ b1;
    x1 = x1 + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x1 = "); disp(x1');
end

代码输出如下：

注意代码中的细节问题：

• 对H矩阵进行分解的时候，实际上是对原始的$H=J^{\prime }J$进行分解，因此要注意把本次求解的时候为了固定第0帧在H矩阵的左上角加的1减掉，也就是代码中 H(1, 1) = H(1, 1) - 1;的操作
• 后面从H矩阵分解$J$和$e$的时候参考了VINS中的做法：注意到sqrt_D矩阵是不可逆的，因为其对角线上有0元素。VINS中的做法是如果不是0的话就求逆，如果是0的话那么这个位置求逆的结果本是无穷大，但是VINS中是直接置为0。
• 注意在使用本次的舒尔补结果进行下次的滑窗优化的时候，仍然需要固定滑窗中的第0帧（也就是$P_1$）的位姿。因为舒尔补结果虽然对状态$P_1,L$有了一个先验因子，但是这个先验因子仍然是从相对测量来的，它是约束了这两个状态和$P_0$之间的相对约束，并不是全局的观测因子，所以下一次滑窗优化尽管加了这个边缘化的先验因子，系统矩阵$H$仍然是不满秩的。同理使用固定第0帧的方式可以发现，此时系统经过一次迭代就达到了最优解。

3.2.VIO或VINS中局部边缘化的方式

这种方式就是在本次滑窗优化之后，只对和要边缘化掉的状态相关的那些状态构成的H矩阵进行舒尔补，也就是只考虑要优化掉的状态构成的残差。然后再进行矩阵的分解得到舒尔补先验的残差和雅克比，并给下一次优化使用。代码如下：

%% schur方式2：vio课件或者vins中的做法
fprintf("-------------------schur方式2----------------------\n");
J_ = [1, 0, -1; 
      1, -1, 0];  % 状态变量: P0 P1 L
r_ = [l0 - (x(4) - x(1));
      e1 - (x(2) - x(1))];
H_ = J_' * J_;
b_ = -J_' * r_;
s_H_ = H_(2:end, 2:end) - H_(2:end, 1) * H_(1, 2:end) / H_(1, 1);  % 手动执行舒尔补
s_b_ = b_(2:end, 1) - H_(2:end, 1) * b_(1) / H_(1, 1);
[V_, D_] = eig(s_H_);   % A*V = V*D, 即 A = V*D*V'(V' = V^-1)
sqrt_D_ = sqrt(D_)
sqrt_D_inv_ = [0, 0; 0 1.0/1.0]; % 这里求逆是根据sqrt_D_结果手动写的
s_J_ = sqrt_D_ * V_';    
s_r_ = -sqrt_D_inv_ * V_' * s_b_;  

%% 舒尔补方式2进行下一次滑窗优化
fprintf("----------舒尔补方式2进行下一次滑窗优化-------------\n");

x2 = [x(2); x(3); x(3) + e3; x(4)];
J2 = [1, -1, 0, 0;
     0, 1, -1, 0;
     1, 0, 0, -1;
     0, 1, 0, -1;
     0, 0, 1, -1;
     s_J_(1,1), 0, 0, s_J_(1,2);
     s_J_(2,1), 0, 0, s_J_(2,2)];
H2 = J2' * J2;
fprintf("rank(H2) = %d\n", rank(H2));  % rank(H2) = 3
H2(1, 1) = H2(1, 1) + 1;

for i = 1 : 2
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r0 = s_J_ * ([x2(1); x2(4)] - [x(2); x(4)]);
    r2 = [e2 - (x2(2) - x2(1));
          e3 - (x2(3) - x2(2));
          l1 - (x2(4) - x2(1));
          l2 - (x2(4) - x2(2));
          l3 - (x2(4) - x2(3));
          s_r_(1) + r0(1);
          s_r_(2) + r0(2)];
    b2 = -J2' * r2;
    delta_x = H2 \ b2;
    x2 = x2 + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x2 = "); disp(x2');
end

代码输出如下：

3.3.两种方式和全局优化方式的对比

对比代码如下：

%% 三种方式精度对比
disp("******************比较精度**********************************");
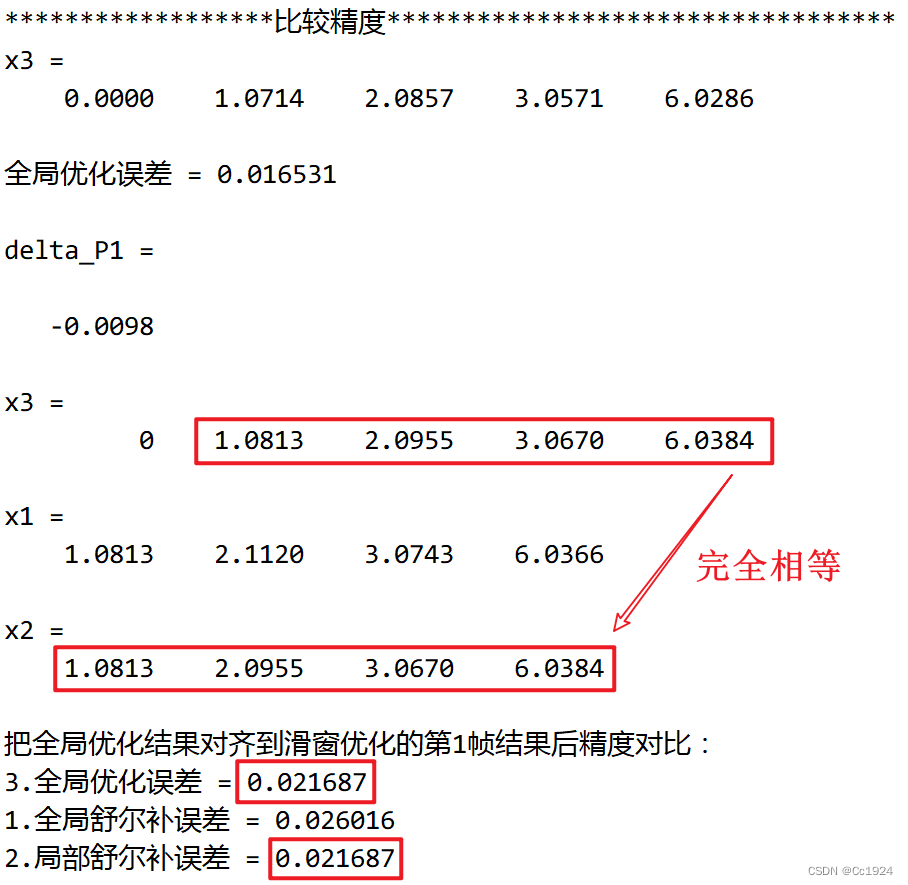
disp("x3 = "); disp(x3');
fprintf("全局优化误差 = %f\n", (x_t3-x3)' * (x_t3-x3));
% 由于使用全局优化的策略，第1帧也会变化；而使用滑窗优化的策略，在第二个滑窗里
% 优化的时候第一帧作为起始帧被固定了，所以这里要把全局优化的第1帧对齐到滑窗优化第1帧上
delta_P1 = x3(2) - x(2)
x3 = x3 - delta_P1;
x3(1) = 0;
disp("x3 = "); disp(x3');
disp("x1 = "); disp(x1');
disp("x2 = "); disp(x2');
fprintf("把全局优化结果对齐到滑窗优化的第1帧结果后精度对比：\n");
fprintf("3.全局优化误差 = %f\n", (x_t3-x3)' * (x_t3-x3));
fprintf("1.全局舒尔补误差 = %f\n", (x_t3-[0; x1])' * (x_t3-[0; x1]));
fprintf("2.局部舒尔补误差 = %f\n", (x_t3-[0; x2])' * (x_t3-[0; x2]));

代码输出：

代码解释：

• 由于不使用滑窗优化而直接进行全局优化的方式，是固定了$P_0$进行优化，也就是$P_1$的位置在优化中仍然是可以变化的。而使用滑窗优化的方式，不论是使用何种舒尔补，在下一次滑窗优化操作中只是先验因子的不同，而由于这些先验因子都是从相对测量来的，所以并不会改变下一次滑窗优化的$H$矩阵的秩，也就是系统仍然是1自由度不可观的。所以下次优化的时候仍然需要固定$P_1$的位姿进行优化。这样就导致如果直接用滑窗优化的结果和全局优化的结果对比的话，他们的初始位置$P_1$不同。所以为了进行对比，手动把全局优化的结果的$P_0$对齐到上一次优化得到的$P_1$上，也就是本次滑窗优化固定的$P_1$上。
• VIO课程或VINS中讲解的局部舒尔补的操作结果和全局优化的结果是一样的！这也就说明了，正确的舒尔布操作是局部舒尔补。
• 对比结果可以发现，全局优化的结果精度是最高的。这个很容易理解，因为全局优化的时候$P_1$的位置仍然可以改变，而滑窗优化中为了固定自由度强行把$P_1$的位置固定了无法进行优化。这样就导致最后尽管使用局部舒尔补得到的滑窗中局部位置之间的相对位置和全局优化的结果是一样的，但是局部舒尔补得到的全局位置有一个偏移，本质上是因为优化时把$P_1$固定了，所以这样导致了误差的产生。

3.4.思考为什么局部舒尔补是对的？

这里还是要从最小二乘的角度来考虑，如下图所示。

局部舒尔补的操作是只考虑边缘化掉的$P_0$构成的残差，然后将这个残差从$P_0——P_1$之间的分布全局转移到$P_1$身上，因为$P_0$将要被滑出边缘化掉。这样在下一次滑窗优化的时候，优化的图如下：

可以看到，使用局部滑窗优化的操作，就相当于把滑出滑窗的$r_0,r_1$两个残差以先验的形式又加入到了当前的图优化中。这样就相当于这次优化的残差仍然是$r_0,r_1,r_2,r_3,r_4,r_5,r_6$所以可以看出来，这种局部舒尔补的操作可以保证在下一次滑窗操作的时候损失函数和全局优化的损失函数保持一致，所以这就是局部舒尔补的滑窗优化得到的相对位姿和全局优化得到的相对位姿完全一致的原因。

而全局舒尔补是对这一次的图优化中的所有残差$r_0,r_1,r_2,r_4,r_5$，把这些残差形成先验因子加到剩下的所有状态变量里。对比局部舒尔补的操作可以发现，这样下一次优化的残差变成了$r_0,r_1,r_2,r_4,r_5+r_2,r_3,r_4,r_5,r_6$，可见残差中重复了一部分$r_2,r_4,r_5$，所以全局舒尔补后进行滑窗优化的损失函数和全局优化的损失函数不一致。

3.5.使用局部残差舒尔补，但是状态变量维度仍然是全局的，有影响吗？

3.5.1.问题引出

上面讲解的正确方法是使用局部舒尔补，注意这个局部有两个意思：一是残差使用的是局部残差，也就是只使用和第0帧有关的残差的雅克比矩阵构成的$H$矩阵进行舒尔补；另外一个局部是在代码中会发现我们维护的$H$矩阵是边缘化掉的状态和保留下的状态构成的最小维度的$H$矩阵，而不是原来的维度的$H$矩阵。这个可以用上面第1次舒尔补边缘化为例进行距离说明，此时要边缘化掉第0帧，第$0$帧构成的局部残差只有两个，并且对应在雅克比矩阵$J$中就是前两行：
$$J=\left[\begin{array}{cccc}1& 0& 0& -1\\ 1& -1& 0& 0\end{array}\right]$$
注意，如果直接使用这个雅克比矩阵的话，里面的状态变量包含了很多和我们本次舒尔补无关的状态变量，因为第0帧构成的残差只和$P_0,P_1,L$有关。我们也可以发现$J$的第3列都是0，因为这两个残差和$P_2$无关。

（1）舒尔补使用原状态变量构成的全局维度的$H$矩阵

如果此时我们直接使用这个雅克比矩阵去计算进行舒尔补的$H$矩阵，显然此时$H$的维度仍然是全部的状态变量的维度，并且由于和$P_2$有关的雅克比全是0，因此最后$H$中$P_2$所在的行和列会组成一个十字的0。计算结果如下，可以看到确实是这样的。
$$H=J^{\prime }J=\left[\begin{array}{cc}1& 1\\ 0& -1\\ 0& 0\\ 0& -1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -1\\ 1& -1& 0& 0\end{array}\right]=\left[\begin{array}{cccc}2& -1& 0& -1\\ -1& 1& 0& 0\\ 0& 0& 0& 0\\ -1& 0& 0& 1\end{array}\right]$$
（2）舒尔补使用相关状态变量构成的最小维度的$H$矩阵

如果说我们按照上面程序中操作的那样，只考虑和残差有关的状态构成的$H$矩阵呢？也就是说此时的雅克比矩阵维度就缩减了，会把和要边缘化掉的残差无关的那些状态直接去掉，从而雅克比变为：
$$J=\left[\begin{array}{ccc}1& 0& -1\\ 1& -1& 0\end{array}\right]$$
那么此时的$H$矩阵就变成$3\times 3$的了，如下：
$$H=J^{\prime }J=\left[\begin{array}{cc}1& 1\\ 0& -1\\ 0& -1\end{array}\right]\left[\begin{array}{ccc}1& 0& -1\\ 1& -1& 0\end{array}\right]=\left[\begin{array}{ccc}2& -1& -1\\ -1& 1& 0\\ -1& 0& 1\end{array}\right]$$
现在的问题是，使用这两种不同维度的$H$矩阵，对最后舒尔补之后的结果再进行分解，得到的对保留状态的先验残差和雅克比是一样的吗？如果使用原状态变量构成的全局维度的$H$矩阵进行舒尔补再分解，会不会对无关的状态变量$P_2$产生额外的雅克比和残差，从而对错误地对$P_2$也产生先验约束？

3.5.2.解答

首先给出上面问题的答案是：不会！无论使用全局维度的$H$还是局部维度的$H$进行舒尔补边缘化，最后都只会对和残差有关的状态变量形成先验约束。

这是为什么呢？去分析全局维度的$H$矩阵的形式我们会发现，由于$H$矩阵中无关的状态变量$P_2$的位置都是0，所以在舒尔补消元（实际就是高斯行消元），并不会对$P_2$所在的行进行高斯消元，所以$P_2$所在的行一直都是0。另外我们是对行进行高斯消元，不会操作列，所以$P_2$所在的列也一直都是0。也就是说，舒尔补并不会改变$H$矩阵中的全0行和全0列，也就是不会改变$P_2$构成的全0的十字。那么这样在舒尔补消元之后，我们得到剩下的矩阵，它一定是如下的形式：

$$s\_H=\left[\begin{array}{ccc}\ast & 0& \ast \\ 0& 0& 0\\ \ast & 0& \ast \end{array}\right]$$

$\ast$是什么数不用管，但是肯定$P_2$构成的全0的十字仍然不变。下面我们要做的就是对$s\_H$进行$L{L}^T$分解，得到雅克比舒尔补之后形成的先验约束的雅克比矩阵$s\_J$。现在假设$s\_J$的形式为
$$s\_J=\left[\begin{array}{ccc}{J}_{11}& J_{12}& J_{13}\\ J_{21}& J_{22}& J_{23}\\ J_{31}& J_{32}& J_{33}\end{array}\right]$$

那么此时应该满足
$$s\_H=s\_J^{\prime }s\_J=s\_J=\left[\begin{array}{ccc}{J}_{11}& J_{21}& J_{31}\\ J_{12}& J_{22}& J_{32}\\ J_{13}& J_{23}& J_{33}\end{array}\right]\left[\begin{array}{ccc}{J}_{11}& J_{12}& J_{13}\\ J_{21}& J_{22}& J_{23}\\ J_{31}& J_{32}& J_{33}\end{array}\right]=\left[\begin{array}{ccc}\ast & 0& \ast \\ 0& 0& 0\\ \ast & 0& \ast \end{array}\right]$$

这里注意到$s\_H(2,2)=J_{12}^2+J_{22}^2+J_{32}^2=0$，所以可以得出$J_{12}=J_{22}=J_{32}=0$，从而最后$s\_J$的形式为：
$$s\_J=\left[\begin{array}{ccc}{J}_{11}& 0& J_{13}\\ J_{21}& 0& J_{23}\\ J_{31}& 0& J_{33}\end{array}\right]$$

注意这个雅克比$s\_J$的行表示舒尔补边缘化对保留下的状态$P_1,P_2,L$的残差，列表示每一个残差的状态变量是$P_1,P_2,P_3$。从上面可以看到，$P_2$这一列都是0，也就是我们边缘化构成的先验约束残差，对状态变量$P_2$的雅克比是0，也就是$P_2$怎么变这个先验约束残差都不会变，即这种舒尔补边缘化的方式对$P_2$并没有构成先验约束。

因此，使用原状态变量维度构成的全局维度的$H$矩阵进行舒尔补最后形成的对状态变量的先验约束和使用局部状态变量构成的$H$矩阵是一样的，但是显然这种方式把$H$矩阵维度变大了，增加了计算量，所以实际代码中都是使用局部状态变量构成的$H$矩阵。

4.几点思考

4.1.再思考滑窗优化中固定滑窗中第0帧的缺点能否改进？

首先为了下面表述的清楚，给一些说法进行定义：

对滑窗中的状态$P_0,P_1,P_2,L$进行非线性优化称为第0次滑窗优化；

对第0次滑窗优化后的结果$P_0,P_1,P_2,L$进行舒尔补消去$P_0$称为第1次舒尔补边缘化；

新来状态$P_3$，对滑窗中状态$P_1,P_2,P_3,L$进行非线性优化称为第1次滑窗优化；

对第1次滑窗优化后的结果$P_1,P_2,P_3,L$进行舒尔补消去$P_1$称为第2次舒尔补边缘化；

新来状态$P_4$，对滑窗中状态$P_2,P_3,P_4,L$进行非线性优化称为第2次滑窗优化。

4.1.1.从上面实验得到的想法

上面实验结果证明，尽管局部舒尔补然后滑窗优化得到的相对位置和全局优化是一样的，但是由于滑窗优化的时候由于系统仍然是1自由度不可观的，所以只能固定住滑窗中第0帧，这样就导致最后优化得到的全局位置相对全局优化有一个偏置。能否修正这个偏置呢？

现在有一个想法，就是我在局部舒尔补的时候，不使用局部雅克比$J^{\prime }J$构成的局部$H$矩阵进行舒尔消元，而是使用$H$矩阵左上角加单位阵，也就是进行方程求解的时候固定了第0帧得到的$H$矩阵进行舒尔消元。这样就相当于我会把全局优化的第0帧是固定的信息通过舒尔补边缘化第0帧构成的残差的形式传递给下一次滑窗优化，这样下一次滑窗优化不就有相当于有了全局观测了吗？这样自然下次滑窗优化的$H$矩阵就是满秩的。

但是实际测试发现，这个操作并不可行。其实这个本质上和求解$H\Delta x=-b$的时候几种不同的固定方式有关。上面说的$H$矩阵左上角加单位阵的操作是一种固定滑窗中第0帧的操作，其实本质上并不适合传递第0帧被固定的信息。而真正适合传递信息的，是使用给第0帧加超强先验约束的方式。

4.1.2.简单总结不同的gauge handle方法

设想在进行第一次优化之后，需要进行边缘化给第二次优化提供边缘化约束。但是第一次优化的时候为了解决1自由度不可观的问题，需要使用某种方式固定自由度。这种存在自由度不可观的情况在论文中成为gauge freedom，处理gauge freedom（称为gauge handle）有多种方式，这篇论文总结为下面三种方式（g2o中还有一种方式，这里定义为第4种）：

1. free gauge ：不管这个自由度，而$H\Delta x=-b$的求解$H$不满秩的问题靠L-M算法中给$H$增加一个$\lambda I$来间接解决（因为本来$\lambda I$是为了限制高斯牛顿法接近二次拟合的）。但是这样的结果最后仍然会在零空间漂移，所以在VINS中用的做法就是使用free gauge求解$\Delta x$，但是求解之后把滑窗中第0帧保持不变。

2. fix gauge：固定滑窗中的第0帧，具体操作就是和滑窗中的第0帧有关的雅克比矩阵全都置为0，这就意味第0帧的变化对所有的残差都不会有贡献，所以第0帧在优化中就不会改变了。从数学上来看，在第0帧的$H$矩阵项是0，$b$项也是0，由于使用LM算法求解，最后就变成了$(0+\lambda I)\Delta x=0$，结果只能是$\Delta x=0$。我感觉这个本质上属于一种数学技巧，并不是很有物理意义。

3. prior gague：给滑窗中的第0帧添加先验，这种方式实际上是最正规的方式，因为它有明确的物理一样，而其他方式更像是一种数学上的技巧。这种添加先验的方式就是从存在不可观的原因出发，即由于测量全都是相对测量而没有绝对测量，导致优化结果可以漂移。所以这种方式就是增加一个绝对位置的先验测量，比如给滑窗中第0帧添加一个先验观测的位置是0，这样优化的时候最终结果就不会离0太远。

   （1）如果想固定第0帧就是在先验观测0的位置，那么只需要把这个先验观测的协方差矩阵设置的非常小，也就是信息矩阵（权重）设置的非常大，这样优化状态离先验观测稍微偏离一点就会造成非常大的误差项，从而最后会把第0帧的优化状态固定在先验的位置。

   （2）如果就是有一个实际观测到的先验，比如GPS观测，有明确的协方差矩阵，那么就可以把它作为先验融合到滑窗优化中，这样滑窗中第0帧位置可能会发生变化，但是此时就是需要让它有变化，因为我们已经有先验了，需要来修正这个状态。

4. g2o tutorial：这种方式也是属于固定第0帧，叫什么名字不知道，在手写VIO的课程中有讲解。其操作就是在最后的$H$矩阵第0帧的位置强行加一个$I$，但是对应的$b$的位置并不加任何东西。这样其实本质上就是更改了原来的$H\Delta x=-b$的方程组，导致求解的结果中$\Delta x_0$只能为0。所以这个本质上也属于一种数学技巧，并没有物理意义。

经过这四种总结可以发现，4.1.1中就是想把上面g2o tutorial的方法的固定信息传递给下一帧。但是这种方法并没有实际的物理意义，最后实验验证也发现如果直接把这种方法得到的最后的$H$矩阵分解的雅克比传递给下一次滑窗优化，尽管下一次滑窗优化的$H$矩阵确实满秩了，但是其行列式非常接近0，也就是其本质上还是非常接近奇异状态的，所以这种方式并不可行。

因此正确的方式应该是使用prior gauge的方法：在第一次滑窗优化的时候给第0帧加一个超强先验，也就是这个先验的信息矩阵非常大，反应在$H$矩阵中就是先验项的贡献的值明显超过其他项。这样在边缘化的时候，由于这个先验残差会通过舒尔补传递给其他状态，这样就导致其他状态也间接有了一个先验，从而解决下一次优化的不满秩问题。

4.1.3.实验验证prior gauge方法传递第0帧固定信息

思路就是4.1.2中说的思路，代码实现如下：

clear all; clc;

%% 1.正常状态，滑窗中维护3个位置+1个路标点
disp("----------1.正常状态，滑窗中维护3个位置+1个路标点--------------");
% 真实状态
x_t = [0; 1; 2; 6];  % 滑窗长度为3, 变量分别为P0, P1, P2, L
% 码盘测量值, e=encoder, l=lidar
l0 = 6.0; e1 = 1.1; e2 = 0.95; l1 = 5.05; l2 = 3.8;
e0 = 0.0;  % 为了解决漂移的问题，给一个超强先验
% 状态初值, 由码盘测量值来得到
P0 = e0; P1 = P0 + e1; P2 = P1 + e2; L = P0 + l0; 
% 状态初始估计值
x = [P0; P1; P2; L]; 

% 雅克比矩阵保持不变, 因为是线性模型
w = 30;   % 超强先验的权重，注意一定是正数。而且这个数值还不能太大，如果太大会导致H矩阵直接退化成rank=1
J = [-w, 0, 0, 0;   % 超强先验, 残差是 w(e0 - P0), 所以雅克比是-w
     1, 0, 0, -1;
     1, -1, 0, 0; 
     0, 1, -1, 0;
     0, 1, 0, -1;
     0, 0, 1, -1];
% 开始构造高斯牛顿的优化问题，认为信息权重矩阵都是I
H = J' * J
fprintf("rank(H) = %d\n", rank(H));  % rank(H) = 4

% 其实由于是线性模型，所以没必要迭代，一步就是最速下降法得到最优解
for i = 1 : 2   
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r = [ w * (e0 - x(1));
         l0 - (x(4) - x(1));
         e1 - (x(2) - x(1)); 
         e2 - (x(3) - x(2));
         l1 - (x(4) - x(2));
         l2 - (x(4) - x(3))];
    b = -J' * r;
    delta_x = H \ b;
    x = x + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x = "); disp(x');
end
fprintf("error = %f\n", (x_t-x)' * (x_t-x));

% 再来一个状态
% 真实状态
x_t3 = [0; 1; 2; 3; 6];  % 状态变量变成4个，分别为P0, P1, P2, P3, L
% 这一次的测量
e3 = 1.05; l3 = 3.05; P3 = P2 + e3; 

%% schur方式2：vio课件或者vins中的做法
fprintf("-------------------schur方式2----------------------\n");
J_ = [-w, 0, 0;
      1, 0, -1; 
      1, -1, 0];  % 状态变量: P0 P1 L
r_ = [w*(e0 - x(1));
      l0 - (x(4) - x(1));
      e1 - (x(2) - x(1))];
H_ = J_' * J_;
b_ = -J_' * r_;
s_H_ = H_(2:end, 2:end) - H_(2:end, 1) * H_(1, 2:end) / H_(1, 1);  % 手动执行舒尔补
s_b_ = b_(2:end, 1) - H_(2:end, 1) * b_(1) / H_(1, 1);
[V_, D_] = eig(s_H_);   % A*V = V*D, 即 A = V*D*V'(V' = V^-1)
sqrt_D_ = sqrt(D_)
sqrt_D_inv_ = inv(sqrt_D_)  % 可逆了
% sqrt_D_inv_ = [0, 0; 0 1.0/1.0];  % 这里求逆是根据sqrt_D_结果手动写的
s_J_ = sqrt_D_ * V_';    
s_r_ = -sqrt_D_inv_ * V_' * s_b_;  
 
%% 舒尔补方式2进行下一次滑窗优化
fprintf("----------舒尔补方式2进行下一次滑窗优化-------------\n");

x2 = [x(2); x(3); x(3) + e3; x(4)];
J2 = [1, -1, 0, 0;
      0, 1, -1, 0;
      1, 0, 0, -1;
      0, 1, 0, -1;
      0, 0, 1, -1;
      s_J_(1,1), 0, 0, s_J_(1,2);
      s_J_(2,1), 0, 0, s_J_(2,2)];
H2 = J2' * J2
fprintf("rank(H2) = %d\n", rank(H2));  % rank(H2) = 4
det(H2)  % 20.95

for i = 1 : 2
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r0 = s_J_ * ([x2(1); x2(4)] - [x(2); x(4)]);
    r2 = [e2 - (x2(2) - x2(1));
          e3 - (x2(3) - x2(2));
          l1 - (x2(4) - x2(1));
          l2 - (x2(4) - x2(2));
          l3 - (x2(4) - x2(3));
          s_r_(1) + r0(1);
          s_r_(2) + r0(2)];
    b2 = -J2' * r2;
    delta_x = H2 \ b2;
    x2 = x2 + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x2 = "); disp(x2');
end

代码输出结果：

注意：

• 代码中增加的先验权重$w$的大小要合适：不能太小，否则起不到固定第0帧的效果；也不能太大，否则会导致最后的$H$矩阵中数值相差太大，反而导致第一次优化的时候$H$矩阵就直接退化成秩为1的矩阵（因为其他数都太小了，相当于最后的矩阵中只有$w^2$这一项）。最合适的大小就是在优化结果固定住第0帧位置不懂的前提下让$w$尽量小，这样在对第一次优化的$H$矩阵进行舒尔补的时候得到的结果才更加能够避免奇异性。

• 代码输出结果可以发现，这种方式在进行舒尔补之后，下一次滑窗的时候加入这个先验，可以把$H2$的秩恢复成4，并且行列式也不是很小，也就是说这个$H2$矩阵的满秩性质是比较稳定的。从迭代结果也可以发现，一步就迭代到了最终结果。

• 再比较这种方式和进行全局优化的最后结果：
  
  可以看到两种优化方式的结果完全相同，难道我发现了新大陆？

4.1.4.思考为何超强先验的舒尔补滑窗优化和全局优化结果一致？

其实本质上，使用超强先验的舒尔补滑窗优化和上面的全局优化在本质上的操作是一样的。现在来思考我们在全局优化的时候求解$H_{all}\Delta x_{all}=-b_{all}$，注意这个时候的$\Delta x$是历史上所有的状态变量，也就是$P_0,P_1,P_2,P_3,L$构成的，所以这里给加了下标$all$。然后如果此时我不是直接求解这个方程，而是对这个方程的$H_{all}$进行舒尔补，只留下$P_1,P_2,P_3,L$构成的$H$矩阵，然后求出来$\Delta x_{P_1,P_2,P_3,L}$之后再反带回去求$\Delta x_{P_0}$。显然这个由于是数学上的操作，结果和直接求解$H_{all}\Delta x_{all}=-b_{all}$完全一样。

但是仔细观察这种方式和我们使用超强先验的舒尔补滑窗优化有什么关系呢？实际上超强先验的舒尔补滑窗优化就是在进行这种操作，它先把超强先验的误差通过舒尔补转移到了剩下的状态上，然后求解剩下的状态。所以本质上它们两个是一样的，这就解释了为什么它们俩的结果完全相同。

4.1.5.使用超强先验的舒尔补滑窗优化等价于全局优化的方式吗？

那么是否意味着我发现了一种使用超强先验的舒尔补滑窗优化来等价全局优化的方式？并不是！我们来看如果又来了一个状态$P_4$，也就是这次舒尔补滑窗优化的结果需要继续进行舒尔补，然后给下一次滑窗优化使用。这个时候就会发现，对第0帧的超强先验只能作用到第1次舒尔补上，而现在进行第2次舒尔补超强先验就不再起作用了。从优化结果来看，$x2 = [1.0714, 2.0857, 3.0571, $ $6.0286]$本质上不还就是一个位置结果吗？如果我对这四个状态$P_1,P_2,P_3,L$舒尔补边缘化掉状态$P_1$，跟我原来对没有使用超强先验得到$x2=[1.0813,2.0955,3.0670,6.0384]$进行舒尔补没有任何区别， 只是他们的结果稍微有点不同而已。造成这个结果的根本原因是在第1次舒尔补之后再进行滑窗优化后，得到的$P_1$不再具有超强先验了。如果此时我故技重施对$P_1$仍然增加一个超强先验再进行第2次舒尔补，那么就相当于我在下一次优化中固定了$P_1$的位置保持不动，这显然和全局优化固定$P_0$的位置保持不同是不一样的。也就是这种方式在第2次滑窗优化的时候，表面上我做的是$P_2,P_3,P_4,L$的滑窗优化，但是由于我使用舒尔补把$P_1$传递给了这次的滑窗，并且我把通过在舒尔补的时候给$P_1$超强先验把这个全局优化的结果中$P_1$的位置进行了固定，所以实际上做的是一个状态变量为$P_1,P_2,P_3,P_4,L$且$P_1$固定的全局优化。而如果此时我考虑真正的全局优化呢？应该是一个**状态变量为$P_0,P_1,P_2,P_3,P_4,L$且固定$P_0$**的全局优化。所以二者是不等价的。

那么在第2次滑窗优化的时候，如果我还想等价于真正的全局优化该怎么做？没办法，只能在舒尔补的时候仍旧考虑整个的$H$矩阵，也就是$P_0,P_1,P_2,P_3,P_4,L$构成的$H$矩阵，并且把$P_0,P_1$的部分都舒尔补消掉，这样才能把$P_0$的超强先验正确的传递到第2次的滑窗优化中。但是这种操作就和4.1.4中解释的一样了，这样其实本质上和全局优化是一样的，也就是我并没有获得滑窗优化的优点（维持计算量），因为我要一直维护所有状态变量构成的$H$矩阵，并且还要对滑窗中之外的那些状态变量进行舒尔补边缘化掉，所以我还是在做一个全局优化。

4.1.6.讨论：如何能在使用滑窗优化的前提下仍然传递第0帧的超强先验呢？

从上一节的分析可以看到，如果滑窗优化想等价于真正的全局优化，就必须一直维护全局状态的$H$矩阵再进行边缘化，但这种操作并不是真正的滑窗。造成这个现象的根本原因是我们在第1次舒尔补并滑窗优化后得到的状态变量$x2=[1.0714,2.0857,3.0571,6.0286]$中，并没有计算$P_1$的置信度。如果我们把$P_1$直接加一个超强先验，那么等价于一个状态变量为$P_1,P_2,P_3,P_4,L$且$P_1$固定的全局优化，而非真正的全局优化。

所以一个自然的想法是，如果能够得到优化结果中$P_1$的置信度，那么在第2次的边缘化中把$P_1$联合它的置信度作为一个先验因子，不就能把$P_0$的超强先验传递下去了吗？

感觉这样是可行的，但是目前还有一下几个疑问：

• 第1次舒尔补并滑窗优化后得到的$P_1$作为先验，它的置信度怎么求解？

  这个部分或许是一个难点，在VINS-Mono中也没有这种操作，在github issue 74中秦通回答没有好的方法（但是好像ceres中有求解置信度的接口）。其实正是因为没有求解优化后的置信度，VINS中认为每一次滑窗优化后的状态都是最准确的，所以滑窗优化后都把状态对齐到了滑窗中的第0帧上，然后下一次最新帧IMU积分的协方差也回归初始值重新开始传播。

• 另外滑窗优化如果能求置信度，按理说滑窗中所有状态都有一个置信度，那么是否应该把$x2$的结果都作为先验加到下一次的滑窗优化中？还是说只增加$P_1$的先验？

  这个地方目前感觉可以解答，应该是只把$P_1$的先验和置信度加到下次优化。原因是我们现在是在进行舒尔补边缘化，参考第1次边缘化时的操作，我们就是想通过在边缘化的时候给这次优化的结果添加一个先验约束和置信度，然后通过边缘化把这个先验约束传递给下一次的滑窗优化，从而解决下一次的滑窗优化中的gauge问题。所以参考第1次边缘化的时候对第0帧添加超强先验的操作，我们只需要在这次边缘化的时候给$P_1$添加一个先验即可，为什么给$P_1$添加先验？因为它即将被边缘化掉，我给它添加先验才能通过舒尔补传递给剩下的状态

• 如果可求置信度的话，$x2$中的$P_2,P_3,L$的结果在下一次优化中能当做先验因子吗？

  这个问题其实和上面的问题有点重复了，实际上是上一个问题没有弄清楚我们是在边缘化的时候添加先验因子，所以自然是谁被边缘化掉给谁添加先验因子。那么现在的问题是如果可以求置信度，那么$P_1$可以作为先验因子通过舒尔补边缘化的方式加入到第2次滑窗优化中起作用，那么能否额也把第1次滑窗优化得到的结果$P_2,P_3,L$作为先验因子加入第2次滑窗优化中？

  其实也不能，这个原因和最上面讲的全局schur的方式有点类似，就是说如果我也把这些状态加进去当做先验因子了，那么本次滑窗优化我考虑的就不是$P_2,P_3,P_4,L$的残差问题了，而是还附加了上一次的残差$P_2,P_3,L$，所以这种操作的损失函数和全局优化的损失函数不一致。

4.2.先验约束能否降低自由度？

其实通过上面的讨论这个答案显而易见了，先验约束是一定可以降低自由度的。这里单独再拿出来说是因为黄国权老师的一篇紧耦合GPS的论文中说在VIO坐标系下添加GPS先验并不能降低自由度，当时就感觉很奇怪想不明白。这里实验验证其实是可以降低自由度的，也许那篇论文中的结论可能是因为考虑了其他因素吧。

clear all; clc;

%% 1.正常状态，滑窗中维护3个位置+1个路标点
disp("----------1.正常状态，滑窗中维护3个位置+1个路标点--------------");
% 真实状态
x_t = [0; 1; 2; 6];  % 滑窗长度为3, 变量分别为P0, P1, P2, L
% 码盘测量值, e=encoder, l=lidar
l0 = 6; e1 = 1.1; e2 = 0.95; l1 = 5.05; l2 = 3.8; m0 = 0.0;
% 状态初值, 由码盘测量值来得到
P0 = m0; P1 = P0 + e1; P2 = P1 + e2; L = P0 + l0; 
% 状态初始估计值
x = [P0; P1; P2; L]; 

% 雅克比矩阵保持不变, 因为是线性模型
J = [1, 0, 0, -1;
     1, -1, 0, 0; 
     0, 1, -1, 0;
     0, 1, 0, -1;
     0, 0, 1, -1;
     1, 0, 0, 0];

% 开始构造高斯牛顿的优化问题，认为信息权重矩阵都是I
H = J' * J
fprintf("rank(H) = %d\n", rank(H));  % rank(H) = 4
det(H)

% 其实由于是线性模型，所以没必要迭代，一步就是最速下降法得到最优解
for i = 1 : 2
    fprintf("第 %d 次迭代\n", i); 
    % 残差
    r = [l0 - (x(4) - x(1));
         e1 - (x(2) - x(1)); 
         e2 - (x(3) - x(2));
         l1 - (x(4) - x(2));
         l2 - (x(4) - x(3));
         x(1) - m0];  % 先验约束的权重是1
    b = -J' * r;
    delta_x = H \ b;
    x = x + delta_x;
    disp("delta_x = "); disp(delta_x');
    disp("x = "); disp(x');
end
fprintf("error = %f\n", (x_t-x)' * (x_t-x));

代码输出如下，可见增加了一个先验因子之后系统就是完全可观的了。

4.3.舒尔补边缘化结果为什么非要分解为J和e的形式？——再探FEJ

4.3.1.问题描述

通过上面对$H$矩阵进行舒尔补边缘化之后，我们得到了对剩下的状态变量的H矩阵。其中以第1次舒尔补边缘化为例，是把和$P_0$的残差构成$H$矩阵、也就是关于$P_0,P_1,L$的$H$矩阵（注意没有$P_2$，因为前面讲解说明了，局部舒尔补才是正确的）中$P_0$部分舒尔补边缘化掉，然后得到由$P_1,L$构成的小$H$矩阵，二者结果如下：

注意这个结果是我们对$P_0$增加了超强先验，所以导致$s\_H\_$是可逆矩阵。然后此时的先验残差进行舒尔补之后的结果如下：

然后我们会首先对$s\_H\_$矩阵进行特征值分解变成$J^{\prime }J$的形式，然后利用$s\_b\_=-J^{\prime }\ast e$再求解出$e$。这是为什么呢？一开始看VINS的代码是因为ceres提供的接口就是$J$和$e$，然后它会自己去算$H$和$b$。但是后来看到r2live中自己写了后端优化，没用ceres的接口，仍然进行了分解，为何？

其实本质上是因为边缘化的先验约束在下一次的滑窗优化中需要更新残差，对应代码中这部分：

 % 残差
 r0 = s_J_ * ([x2(1); x2(4)] - [x(2); x(4)]);
 r2 = [e2 - (x2(2) - x2(1));
       e3 - (x2(3) - x2(2));
       l1 - (x2(4) - x2(1));
       l2 - (x2(4) - x2(2));
       l3 - (x2(4) - x2(3));
       s_r_(1) + r0(1);
       s_r_(2) + r0(2)];

4.3.2.FEJ操作（貌似下面的讲解也并不是真正的FEJ？看VIO中讲解FEJ）

也就是说，第1次边缘化得到了对剩余状态的一个先验位置约束，这里以边缘化掉$P_0$对$P_1$产生的先验约束$P_1^0$为例，右上角的0代表先验约束。注意我们分解出来的$e$本质上是在第0次滑窗优化之后我们得到的状态$P_1^0$距离真实状态仍然存在的残差。因为我们进行的是一个最小二乘问题，结果是让所有状态的残差平方和最小，而不能保证每一个状态的残差都是0。这个残差可以定义为$e_0=J_0$$\cdot (P_1^0-P_1^t)$，其中$P_1^t$是真实状态。这里为什么前面加了一个雅克比矩阵$J$呢？其实本质上是因为我们分解出的残差并不就是单单的$(P_1^0-P_1^t)$这么简单，更确切的说分解出来的$J、e$并没有很明确的物理意义，并不是像我们上面说的那样就是对状态值的一个先验，这种说法只是我们对最终分解结果的一个物理解释，或者说可视化理解。而实际上由于我们分解出来有一个雅克比矩阵，所以分解出来的残差应该写成$e_0=J_0(P_1^0-P_1^t)$。然后我们分解出来的$J$本质上就是这个残差$e$对我们得到的优化的状态变量$P_1^0$的雅克比，注意这里的$P_1^0$虽然是一个具体的数值，但是在第0次滑窗优化过程中它是改变的，只不过优化的结果是$P_1^0$，在这个点的残差对优化变量的雅克比矩阵也就变成了$J_0={\frac{\partial J_0(P_1-P_1^t)}{\partial P_1}|}_{P_1=P_1^0}$

这样在第1次滑窗优化的时候，如果优化过程中的$P_1$产生了一些变化，那么我的残差仍然是$e=J(P_1-P_1^t)$的形式，但是问题在于本质上我并不知道$P_1^t$是多少，但是我知道第1次边缘化的时候的结果定义了一个残差$e_0$，那么我就可以在这次滑窗优化的过程中把先验约束的残差$e$用$e_0$来间接表示。另外的一个问题是，由于我这个残差并没有明确的公式来表示，而是通过第1次舒尔补边缘化得到的一个数值，所以在第1次滑窗优化过程中我就没办法再去求它对状态变量的雅克比在优化点的值，即在$P_1^1$点的雅克比$J_1={\frac{\partial J(P_1-P_1^t)}{\partial P_1}|}_{P_1=P_1^1}$我是无法知道的。但是可以知道，$P_1^1$的值不会离$P_1^0$太远，所以我可以用$J_0$来近似$J_1$，这也是一个无奈之举。解决了这两个问题后，我们就可以表示在第1次滑窗优化过程中的先验残差了，即：
$$e=J_0(P_1-P_1^t)=J_0{P}_1-(J_0{P}_1^0-e_0)=e_0+J_0(P_1-P_1^0)$$
到这里，一方面解释了VINS中的操作，即为什么不更新先验的雅克比，但是更新残差。这里暂且称为这个操作是FEJ吧，但是VIO的课中好像不是这么讲的。另外一方面，也解释了为什么非要分解出$J$，本质上就是因为在残差更新的时候还需要用到$J$。