平行泊车系统路径规划（3）

5、泊车路径选取

传统的平行泊车路径规划方法是基于两段圆弧进行研究，两段圆弧组成的泊车路径结构简单，如下图所示。方法是将泊车路径简化为两段圆弧，但是两段圆弧相交处的曲率存在突变情况，车辆跟踪路径时，如果停车原地转向的位置与理论圆弧相交点存在偏差，则可能导致泊车失败，而且该方法并不适用于不同的起始点，当起始位置改变时，会增加车辆与周围障碍物发生碰撞的可能性。

另一种平行泊车的路径规划方法是基于圆弧-直线-圆弧进行研究，如下图所示，它在两段圆弧的基础上进行了改进，在两段圆弧之间增加了一条直线作为过渡，减缓了路径曲率突变的情况，相比两段圆弧法，当车辆的初始位置发生改变时，可以通过调节直线 改变泊车路径，使得路径满足避障条件。

基于两段圆弧和圆弧-直线-圆弧规划的泊车路径，都存在路径曲率不连续、需要停车原地转向的问题，这将会增加转向机构的负担以及加剧轮胎的磨损。为了使泊车路径满足曲率连续的要求，许多国内外学者采用曲线拟合的方式去拟合泊车路径，如采用反正切函数作为泊车路径，函数的基本形式如下所示：

式中： a,b,c,d都是决定函数形状的参数，通过改变参数去拟合原来的圆弧路径。虽然反正切函数路径曲线曲率连续，但路径起始点和终止点的曲率都不趋于零。
另外还有采用回旋曲线、B样条曲线和五次多项式曲线来拟合泊车路径，曲线在极坐标下的基本表达式为：

B样条曲线的基本表达形式如下所示：

五次多项式曲线的基本表达形式如下所示：

除了上述几种曲线拟合的表达式以外，应用于车辆换道轨迹的等速偏移和正弦函数叠加的曲线也可用作平行泊车路径，该曲线结合了等速偏移函数侧向加速度恒为零的优点和正弦函数平滑的优点，曲线的基本表达式为：

综合考虑上述几种路径曲线的优缺点，如下表所示。由表可知，为了保证车辆在泊车起始点和终止点位置时，车身姿态与车位保持平行，前轮转角为回正状态，并且为了避免原地转向的情况发生，五次多项式曲线和等速偏移和正弦函数的叠加曲线能够满足条件，但是经过对比函数表达式可以发现，在相同条件下五次多项式曲线的曲率变化速率更快，对车辆的转向机构要求更高，因此本文选用等速偏移和正弦函数的叠加曲线作为泊车路径，如下图所示。

6、泊车约束条件分析

车辆在泊车过程中，不仅要保证车辆能顺利跟踪期望路径，还要保证跟踪过程中的安全性，因此需要考虑泊车过程的避撞约束条件和期望路径的可跟踪性。
6.1 车辆避撞约束条件
由于上文最终确定的泊车路径曲线与圆弧-直线-圆弧路径不同，车辆发生碰撞的约束条件也变得更加复杂。在泊车过程中，最容易与车辆发生碰撞的地方就是车位边界处和道路边界处，综合考虑各种碰撞情况，列举出了车辆可能发生碰撞的六种情况，如下图所示。

从上图可知，为了避免车辆与周围障碍物发生碰撞，泊车路径需要满足以下约束条件：

6.2 参考路径约束条件
为了保证路径的可跟踪性，泊车路径需要满足车辆自身运动学约束条件，约束条件主要有曲率和等效前轮转角转速的约束：
（1）曲率约束：路径的曲率约束主要与车辆后轴中心的最小转弯半径有关，由于泊车路径是依据车辆后轴中心的行驶轨迹进行规划，因此路径曲率不能超过最小转弯半径对应的曲率，即要求路径的最大曲率：

路径曲率计算公式如下所示：

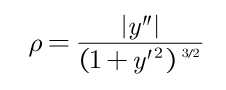
（2）等效前轮转角转速约束：如果路径的等效前轮转角转速超过了车辆转向机构允许的极限范围，那么车辆将不能很好的跟踪期望路径[ ]，因此需要对路径的等效前轮转角转速进行约束，即：

根据阿克曼转向几何关系可得：

根据上式可以计算出路径的等效前轮转角：

可以计算出路径等效前轮转角转速：

根据上式可知，路径等效前轮转角转速是与泊车车速有关。当车速发生变化时，路径的等效前轮转角转速也会随之改变，因此为了保证车速改变时路径也具有可跟踪性，上述的计算结果需要按照泊车过程允许的最高车速进行计算，改写上式如下：