【数值分析Ⅰ】第二章：非线性方程求根方法

ElegantCodingWH

已于 2022-12-15 11:39:35 修改

阅读量1.2k

点赞数 3

分类专栏： # 数值分析 Ⅰ 文章标签：算法人工智能

于 2022-11-07 10:37:41 首次发布

本文链接：https://blog.csdn.net/qq_43546676/article/details/127316496

版权

数值分析 Ⅰ 专栏收录该内容

4 篇文章

订阅专栏

文章目录

1. 基本概念
2. 区间法
- 2.1 二分法
3. 迭代法
- 3.1 简单迭代法
- 3.2 牛顿迭代法 (Newton)

1. 基本概念

什么是非线性方程？

对于线性方程，可以使用线性代数求得精确解，所以不需要求近似解。而非线性方程大部分没有求根公式，故只能求近似根。所以接下来的求解对象都是非线性方程。
非线性方程如何求近似解？
1. 求近似根的三步 / 三要素：
  ① 保证根存在；
  ② 确定根的范围；
  ③ 采用 迭代法 或 区间法 构造根的收敛数列 来逐步提高根的精度。
2. 如何衡量不同方法求得的近似根的好坏？
  - 第一个标准是：误差(用于衡量近似解的精确度，误差越小，近似解越精确)
  - 第二个标准是：收敛阶(用于衡量求得近似解的快慢，收敛阶越大，收敛越快，算法越好)
    - 求收敛阶：
    - 收敛阶分类数列：

2. 区间法

2.1 二分法

理论依据：零点定理
满足什么条件才能使用二分法？
算法：
如何衡量求得近似解的好坏？
1. 误差估计：用于衡量近似解的精确度，误差越小，近似解越精确。有两种方式估计误差
  1. 事先估计：k往往偏大，主要用于理论估计
  2. 事后估计：k往往偏小，主要用于实际控制
2. 收敛阶：用于衡量求得近似解的快慢，收敛阶越大，收敛越快，算法越好。因为二分法产生迭代数列的函数一样，所以采用二分法的收敛阶相同，此时的收敛阶没有太大意义。

相关题目：

例题1：使用二分法求近似值

例题2：求二分次数—>使用 事先误差 公式建立不等式求解 【若为小数向上取整，因为分的次数越多越准确】

3. 迭代法

3.1 简单迭代法

理论依据：对方程 f(x)=0 做恒等变换根不发生变化
满足什么条件才能使用迭代法？
- 问题1：一个方程恒等变形得到的所有不动点方程构造的迭代数列都收敛吗？答案：否。比如：
- 问题2：如果不动点方程构造的迭代数列收敛，那么就一定能找到根吗？答：是。
- 故只有构造的迭代数列收敛才可以使用迭代法。那么如何证明构造的迭代数列收敛？充分条件如下：
  其中[a, b]表示根在哪个范围内，a, b的值如何确定？
  1. 如果题目没有给根的范围：根据不动点方程或不动点方程恒等变形，转为两个图像的交点，这样就能确定a, b的值。
  2. 如果题目给了根的范围，则将所有式子放到一边，构造f(x)去试
算法：
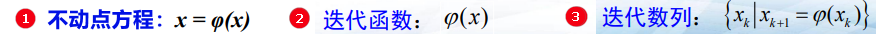
- 其中产生了3个专有名词：不动点方程、迭代函数、迭代数列
如何衡量求得解的好坏？
1. 误差估计：用于衡量近似解的精确度，误差越小，近似解越精确。有两种方式估计误差
  1. 事先估计：k往往偏大，主要用于理论估计
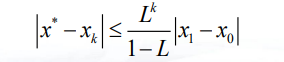
  2. 事后估计：k往往偏小，主要用于实际控制
2. 收敛阶：用于衡量求得近似解的快慢，收敛阶越大，收敛越快，算法越好。由于迭代法的迭代函数可能不同，导致收敛速度不同，所以收敛阶在迭代法中很重要。
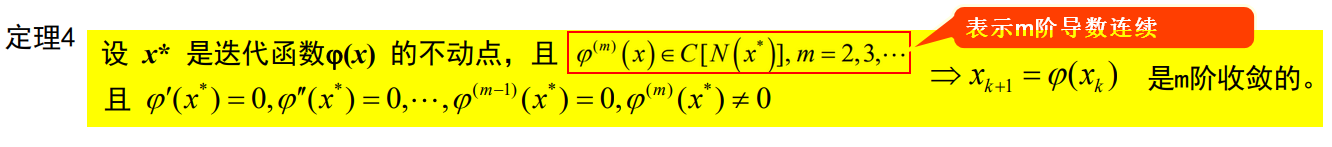
  注意：
  1. 上面定义的证明过程：
  2. 根据上面定理易知：
  3. 如果迭代函数为分式，不好求导时，可以利用不动点方程，转为隐式求导。
算法如何优化？
- 增量松弛加速方法：
  ① 可以加快收敛速度；
  ② 可以将部分不收敛的迭代数列变的收敛。
  
  改进原理如下：

相关题目：

例题1：证明迭代数列收敛

例题2：无论是求迭代公式还是利用迭代公式求解，都必须先证明满足使用迭代法的条件。

利用迭代法求近似解

收敛阶相关题目
用收敛阶定理解题

用收敛阶定义解题

3.2 牛顿迭代法 (Newton)

思想：将函数做线性化处理，把方程转化为对应的近似方程，再构造迭代公式。

虽然这样感觉误差会很大，但是实际上效果却非常好：
① 不仅迭代次数更少，即更快的找到近似解
② 而且求得的近似解一般精度都很高
满足什么条件才能使用牛顿迭代法？
- 仍然是迭代数列收敛。那么如何判断迭代函数收敛？充分条件如下：
算法
迭代法的几何意义：
如何衡量求得近似值的好坏？
1. 误差
2. 收敛阶：由于产生迭代数列的函数一样，所以收敛阶都一样，和二分法一样，此时收敛阶并无太大意义。但是其收敛阶至少是平分收敛的。
非线性方程组求近似解的迭代公式