（2024|ICLR，DDBM，基于分数的 ODE 和 SDE，Doob 的 h 变换）去噪扩散桥模型

最新推荐文章于 2025-03-08 20:06:27 发布

EDPJ，公众号（EDPJ）

最新推荐文章于 2025-03-08 20:06:27 发布

阅读量2.5k

点赞数 23

分类专栏：论文笔记文章标签：计算机视觉人工智能

本文链接：https://blog.csdn.net/qq_44681809/article/details/136024292

版权

论文笔记专栏收录该内容

356 篇文章

订阅专栏

Denoising Diffusion Bridge Models

公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

3.1 时间反转的 SDE 和概率流 ODE

0. 摘要

扩散模型是强大的生成模型，使用随机过程将噪声映射到数据。然而，对于诸如图像编辑之类的许多应用，模型输入并非来自随机噪声的分布。因此，扩散模型必须依赖繁琐的方法，如引导或投影抽样，以将此信息纳入生成过程。在我们的工作中，我们提出去噪扩散桥模型（Denoising Diffusion Bridge Models，DDBMs），这是一种基于扩散桥（diffusion bridges）的范例，它是一组在给定为端点的两个配对分布之间插值的过程。我们的方法从数据中学习扩散桥的分数，并通过求解基于学习分数的（随机）微分方程，从一个端点分布映射到另一个端点分布。我们的方法自然地统一了几类生成模型，如基于分数的扩散模型和 OT-Flow-Matching，使我们能够调整现有的设计和架构选择以适应我们更一般的问题。在实证方面，我们将 DDBMs 应用于像素空间和潜在空间中的具有挑战性的图像数据集。在标准图像翻译问题上，DDBMs 相对于基线方法取得了显著的改进，当我们将问题简化为通过将源分布设置为随机噪声来进行图像生成时，尽管 DDBMs 是为更一般的任务而构建的，但在 FID 分数上与最先进的方法相当。

2024 ICLR OpenReview：https://openreview.net/forum?id=FKksTayvGo&noteId=4w9lJUTXa8

2. 基础

2.1 扩散模型生成建模

扩散过程。我们有兴趣对分布 q_data(x)， x ∈ R^d 进行建模。我们通过构建一个扩散过程来实现这一点，该过程由一组时间索引变量 {x_t}^T_(t=0) 表示，使得

这里 q_data(x) 是初始的 “数据” 分布，p_prior(x) 是最终的 “先验” 分布。该过程可以建模为以下

SDE 的解：

其中 f：R^d×[0, T] → R^d 是矢量值漂移函数，g：[0, T] → R是标量值扩散系数，w_t 是维纳过程。按照这个扩散过程向前推进时间，限制了最终变量 x_T 遵循分布 p_prior(x)。这个过程的反向是通过以下方式给出的：

其中 p(x_t) := p(x_t, t) 是时间 t 时 x_t 的边际分布。此外，可以推导出一个等价的确定性过程，称为概率流 ODE（Song等人，2020b），其具有相同的边际分布：

特别是，可通过反向时间解决上述逆 SDE 或 ODE，来获得 x_T ∼ q_data(y) 并抽样 q_data。

去噪分数匹配。分数 ∇_(x_t) log p(x_t) 可以通过分数匹配损失学习：

其中上述损失的最小化器 s*_θ (x_t, t) 近似于真实分数。至关重要的是，因为过渡核（transition kernel） p(xt | x0)，上述损失是可行的，它取决于漂移和扩散函数的具体选择，被设计为高斯 xt = αt·x0 + σt·ϵ，其中 αt 和 σt 是时间和 ϵ ∼ N(0, I) 的函数。通常还将扩散过程视为 xt 的信噪比（SNR），定义为α^2_t / σ^2_t。

2.2 具有固定端点的扩散过程

扩散模型的局限性在于它们只能将复杂数据分布转换到标准高斯分布，并且无法自然地在两个任意分布之间进行转换，例如在图像到图像的翻译的情况下。幸运的是，经典结果表明，可以通过著名的 Doob 的 h 变换将扩散过程置于已知固定端点上：

通过 h-transform 的随机桥。具体来说，通过 Doob 的 h 变换（Doob和Doob，1984; Rogers和Williams，2000），在公式（1）中定义的扩散过程可以被驱动到达感兴趣的特定端点 y ∈ R^d，

其中 h 是由原始 SDE 生成的从 t 到 T 的过渡核的对数，以点 x_t = x 和 x_T = y 评估，并且每个 x_t 现在在时间 T 明确依赖于 y。此外，p(x_T = y | x_t) 满足 Kolmogorov 反向方程（在附录 A 中指定）。通过具体的漂移和扩散选择，例如 f(xt, t) = 0，由于底层扩散过程的可行（高斯）过渡核，h 是可行的。

当初始点 x0 固定时，该过程通常被称为扩散桥（Särkkä和Solin，2019; Heng等，2021; Delyon和Hu，2006; Schauer等，2017; Peluchetti; Liu等，2022b），其连接任何给定 x0 到给定的 xT 值的能力对于图像到图像的翻译是有希望的。此外，过渡核可能是可行的，这进一步作为动机。

3. 去噪扩散桥模型

假设扩散桥的端点都存在于 Rd 中，并来自任意和未知的联合分布，即

我们希望设计一个过程，给定从 q_data(x, y) 中抽取的一组成对样本的训练集，通过反转边界分布 q_data(x, y) 的扩散桥，学会从 q_data(x | y) 中近似抽样。

3.1 时间反转的 SDE 和概率流 ODE

受到扩散桥的启发，我们构造具有边际分布 p(xt) 的随机过程 {xt}^T_(t=0)，使得 p(x0, xT) 近似于q_data(x0, xT)。反转过程等同于从 q(xt | xT) 中抽样。请注意，分布 q(·) 与 p(·)（即扩散边际分布）不同，因为端点分布现在是 q_data(x0, xT) = q_data(x, y)，而不是扩散分布

它定义了给定 x0 时的高斯 xT。我们可以通过以下定理构造 q(xt | xT) 的时间反转 SDE / 概率流ODE。

定理1。条件概率 q(xt | xT) 的演变具有如下形式的时间反转 SDE：

其相关的概率流 ODE：

在 t ≤ T − ϵ 对于任意 ϵ > 0，其中 ^wt 表示维纳过程

h 如公式（5）定义。

桥过程的示意图如图 1 所示。请注意，此过程定义了直到 T−ϵ。为了在 SDE 的情况下恢复初始分布，我们做一个近似，即 xT − ϵ ≈ y 对于一些小的 ϵ，以逆向模拟逆 SDE。对于 ODE 的情况，由于我们需要从不是 Dirac delta 的 p(x_(T−ϵ)) 中抽样，我们不能用单个 y 近似 x_(T−ϵ)。相反，我们可以首先近似 x_(T−ϵ′) ≈ y 其中 ϵ > ϵ′ > 0，然后对 x_(T−ϵ) 进行 Euler-Maruyama 步骤，之后可以使用公式（7）。图 2 显示了 VE 桥和 VP 桥的简单示例可视化。顶部和底部显示了 VE 和 VP 桥的 SDE 和 ODE 路径。

3.2 边际分布和去噪桥分数匹配

定理 1 中的采样过程需要近似得分

然而，由于真实分数未知，我们受到去噪分数匹配（Song等人，2020b）的启发，使用神经网络通过与可行数量匹配来近似真实分数。这通常导致给定数据（例如在扩散模型的情况下为 x0，我们的情况为（x0，xT））的闭合形式边际抽样，并且给定 xt，模型经过训练以匹配闭合形式的去噪分数目标。我们受到相似方法的启发，因为（1）可行的 xt 边际抽样和（2）闭合形式的目标使得算法简单且可扩展。我们在下面详细说明如何设计边际抽样分布和可行的分数目标，以近似地获取地真实条件分数 ∇_(xt) logq(xt∣xT) 。

抽样分布。幸运的是，对于前者的条件，我们可以设计我们的抽样分布 q(⋅) ，使得 q(xt∣x0,xT) :=p(xt∣x0,xT) ，其中 p(⋅) 是固定在两个端点的扩散分布，如公式（5）所示。对于具有高斯过渡核的扩散过程，例如 VE，VP（Song等人，2020b），我们的抽样分布是以下形式的高斯分布：

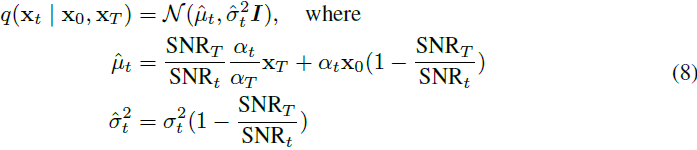
其中 αt 和 σt 是预定义的信号和噪声调度，SNR_t = α^2_t / σ^2_t 是时间 t 的信噪比。对于 VE 进度，我们假设 αt = 1，在附录 A.1 中提供了推导细节。值得注意的是，这个分布的均值是两个（缩放的）端点之间的线性插值，当接近任一端时，分布趋近于 Dirac 分布。为了具体起见，我们在表 1 中展示了由 VP 和 VE 扩散生成的桥过程，并建议选择其中规定的 f 和 g。

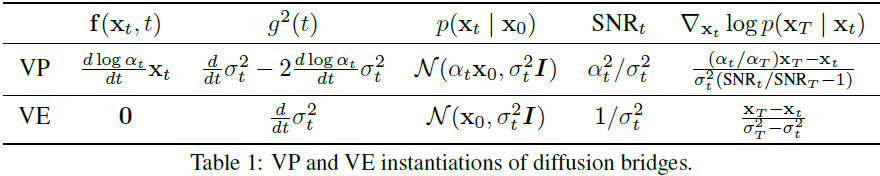
训练目标。对于后者的条件，扩散桥受益于与扩散模型中相似的设置，因为预定义的信号/噪声进度导致了闭合形式的条件分数 ∇_(xt) logq(xt∣x0,xT)。我们在以下定理中展示，通过 xt ∼ q(xt∣x0,xT)，与这个闭合形式分数匹配的神经网络 sθ(xt,xT,t) 近似于真实分数。

定理 2（去噪桥分数匹配）。设（x0，xT）∼ qdata（x，y），xt ∼ q（xt | x0，xT），t ∼ p（t），其中 p(t) 是 [0，T] 中的任何非零时间抽样分布，w(t) 是任意选择的非零损失加权项。以下目标的最小值：

满足 s_θ(xt,xT,t) = ∇_(xt) log q(xt | xT)。

简而言之，我们建立了一个可处理的扩散桥，连接了两个端点，并通过匹配高斯桥的条件得分，我们可以学习新分布 q(xt | xT) 的得分，该分布满足边界分布 q_data(x，y)。

4. 分布翻译的广义参数化

5. 针对降噪扩散桥的随机抽样

6. 相关工作和特殊情况

扩散桥、薛定谔桥和 Doob 的 h 变换。

扩散桥（Särkkä和Solin，2019）是概率论中的常见工具，在最近几年中在生成建模的背景下得到了积极研究（Liu等，2022b；Somnath等，2023；De Bortoli等，2021；Peluchetti，2023）。

给定分数的近似值 ∇xt log p(xt)，Heng 等（2021）研究了在固定起始/结束点条件下的扩散桥，并学习模拟桥的时间逆转。
最近，刘等人（2022b）不考虑具有固定端点的桥，而是使用 Doob 的 h 变换在任意分布之间建立桥梁。通过在训练期间模拟整个路径来学习正向桥。
相反，其他工作（Somnath等，2023；Peluchetti），虽然也采用了 Doob 的 h 变换，但提出了用于正向生成的无模拟算法。
Delbracio 和 Milanfar（2023）同样构建了一个布朗桥（Brownian Bridge）进行直接迭代，并成功应用于图像恢复任务。

另一种方法 De Bortoli 等（2021）提出了迭代比例拟合（Iterative Proportional Fitting，IPF）来可行地解决薛定谔桥（Schödinger Bridge，SB）问题，用于在不同分布之间进行转换。

刘等人（2023）建立在一类可行的 SB 上，导致无模拟算法，并在图像翻译任务中表现出色。
最近，通过将 IPF 与 SB 扩展，Bridge-Matching（Shi等，2023）提出使用迭代马尔可夫拟合来解决 SB 问题。Peluchetti（2023）也为分布翻译开发了类似的算法。

与我们更相关的工作是 Li 等（2023），该工作提出直接在离散时间内逆转布朗桥进行分布转换。相反，我们的方法展示了如何从连续时间中的任何现有 VP 和 VE 扩散过程构建桥梁模型，而布朗桥（在大多数先前的工作中考虑过）只是 VE 桥的一种特殊情况。

我们还展示了，正确实施时，VP 桥可以达到非常强大的经验性能。尽管可以使用与 Peluchetti 中的正向时间扩散相同的观点派生类似的观点，该观点还提出了 VE/VP 桥调度，但我们的框架在经验（重用扩散设计）和理论（与 OT-Flow-Matching（Lipman等，2023；Tong等，2023b）以及Rectified Flow（Liu等，2022a）的联系）上都具有额外的优势。

流和最优输运（Flow and Optimal Transport，OT）。

基于流匹配（Flow-Matching）（Lipman等，2023；Tong等，2023b；Pooladian等，2023；Tong等，2023a）的工作学习基于 ODE 的输运映射来桥接两个分布。