积分电路和滤波电路的主要区别点和应用场合

学工科的皮皮志^_^

已于 2024-09-17 00:45:09 修改

阅读量2.6k

点赞数 14

分类专栏：模拟电路文章标签：嵌入式硬件经验分享学习积分电路模拟电路

于 2024-09-17 00:44:55 首次发布

本文链接：https://blog.csdn.net/qq_45138815/article/details/142309119

版权

模拟电路专栏收录该内容

18 篇文章

订阅专栏

文章目录

前言
一、滤波电路的分类
二、有源滤波器和无源滤波器的优缺点和实用范围
三、积分电路
四、无源RC低通滤波器
- - 4.3.1 截止频率推导
  - 4.3.2 无源积分电路和无源滤波器的关系
五、有源积分电路
总结

前言

本文从滤波器的分类作为切入点，将滤波器分为有源滤波器和无源滤波器，它们之间又涵盖了有源积分电路和无源积分电路，从而引出积分电路这个话题，以RC充放电的电路响应，来解释了无源积分电路的原理。
后文通过对无源RC低通滤波器和有源RC低通滤波器的公式推导，来解释为什么
无源积分电路和有源积分电路也属于一种低通滤波电路，讲述了积分电路的用途，积分电路常用于波形转换，如将矩形波变三角波。对正弦波积分可以实现相移，最后总结了它们的异同点。

一、滤波电路的分类

滤波电路可以分为两大类，无源滤波电路和有源滤波电路，他们都包含常用的低通、高通，带通，带阻等滤波电路，有源滤波电路需要使用放大器等有源元件来增强信号，而无源滤波电路则不需要使用这些元件，若滤波电路仅由无源元件（电阻、电容、电感）组成，则称为无源滤波电路。若滤波电路由无源元件和有源元件（双极型管、单极型管、集成运放）共同组成，则称为有源滤波电路。。滤波器的分类如下图1所示。
在这里插入图片描述
图1 有源滤波器和无源滤波器

二、有源滤波器和无源滤波器的优缺点和实用范围

有源滤波器的设计一般基于运算放大器及其外围电路的组合，外围电路可以是 RC 网络，也可以是 LC 网络。滤波器形式多样，比如贝塞尔，巴特沃思，切比雪夫和椭圆等。
无源滤波器则一般基于RC和LC 网络的设计。不同于有源的是 RC和LC 网络需要做端接阻抗匹配。
对于这两大类滤波器，实际中如何进行选择呢？我们可以从实际输入信号频率来进行选择。如图2所示。
在这里插入图片描述
图2
有源滤波器适用在低频段（<100K）的滤波.当频率较低时，若用无源的话，电容，电感的元件值及体积都会很大，大电容和大电感不易获得，且误差较大。而有源滤波器则可以依靠运放在低频段的诸多优势（尤其是低噪声运放）达到很好的滤波效果。首先，运放本身是由三极管网络搭建而成，而这个网络呈现的特性就是一低通滤波器，对高频信号衰减很快，其频响曲线会在芯片资料中有详细说明，比如 Op07，如下图3所示，对 100K 以上的正弦信号便会作很大衰减。再是，有源滤波器外围是 RC 网络，设计简单，一般不会受分布电抗的影响，而无源滤波器由于存在 LC 网络，自然容易受板间分布电抗的影响，还会产生 LC 自激振荡现象；再者无源滤波器对信号有固定的衰减，仍需靠运放作增益补偿。还有，无源滤波器需要做标准的端接阻抗匹配，增加了与相邻电路连接的难度，而有源滤波器则不用刻意的去做，因为运放一般输入阻抗很高，输出阻抗小，具有缓冲作用，与外围电路连接就比较容易。所以在低频段能够用运放的尽量用运放设计有源滤波器。
在这里插入图片描述
图3 OP07的开环频率增益响应
而当频率较高时（>100K），无源滤波器就体现出其优势。因为，运放受到增益带宽积及其摆率的限制，不能通过较高的频率。若采用高速运放，成本太高，且会引入较大的电源噪声。相反，由于频率高了之后，无源滤波器的元件参数值都会变小，体积也就小了；再是，由于无需运放，也不接入电源，则电路简单，连接方便，且不会引入电源噪声；不过考虑到电路板分布参数的影响，连接电容电感时，最好不要将各分立元件靠的太近，接线要短而粗。

三、积分电路

积分电路分为无源积分电路和有源积分电路，若滤波电路仅由无源元件（电阻、电容、电感）组成，则称为无源滤波电路。若滤波电路由无源元件和有源元件（双极型管、单极型管、集成运放）共同组成，则称为有源滤波电路。如图4所示
在这里插入图片描述
图4

3.1 无源积分电路

如图5所示的积分电路。这个电路比较容易理解，就是利用电容两端电压不能突变的原理，当U1=A时，给电容C充电，U2逐渐增加；当U1=0时，电容C通过电阻R放电，U2逐渐降低，循环往复。积分电路可以用来将矩形波变成锯齿波输出，成立的条件是时间常数RC>>tp，否则电压C将会出现电压饱和。
在这里插入图片描述
上述电路也常作为低通滤波器使用，那么什么时候是积分电路，什么时候是滤波电路？这取决于输入信号的类型。
前面我们也提到积分电路可以用来将矩形波变成锯齿波输出，那么这个矩形波就是一个阶跃电压。那么当我的输入信号是一个阶跃信号的时候，经过如图5所示的电路，实际上就是一个RC电路的充放电过程。RC电路的充放电过程在每一个大学的教材里，都有非常详细的讲解，引入了一个时间常数τ＝RC。我这里进行简单的介绍。

3.2 RC充放电的电路响应

RC电路主要关注的有三个响应，分别是零状态，零输入，以及全响应。

3.2.1 RC电路的零状态响应

零状态响应:
储能元件的初始能量为零，仅由电源激励所产生的电路的响应。
实质：RC电路的充电过程
在这里插入图片描述
图7

图8

图9

图10

在t等于0时电流最大：
零状态响应：电路的储能元器件（电容、电感类元件）无初始储能,仅由外部激励作用而产生的响应.
电容器上的电压是与激励源对抗的：
ic = (Us - Uc) / R
t = 0 时,储能 Q = 0 , Uc = Q / C = 0 ,ic = Us / R ,是最大值.
在这里插入图片描述
图12

3.2.2 RC电路的零输入响应

零输入响应：
电源激励,输入信号为零,仅由电容元件的初始储能所产生的电路的响应。
实质：RC电路的放电过程
在这里插入图片描述
图13

图14

图15

图16

3.2.3 RC电路的全响应

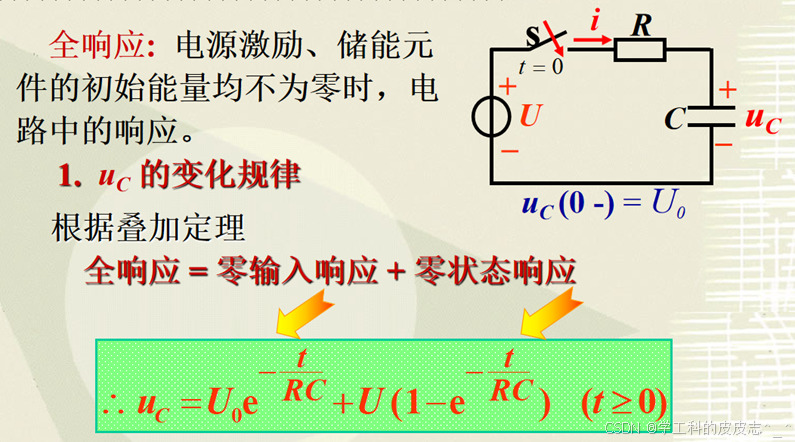
在这里插入图片描述

需要记住什么是稳态分量，什么是暂态分量，什么是稳态值，什么是初始值。

每一个元素的含义
U：代表稳态解
U0代表换路之后的初始值
R:储能元件两端所求得的无源二端网络的等效电阻。
无源二端网络，从储能元件的两端看过去。分清谁与谁串并联
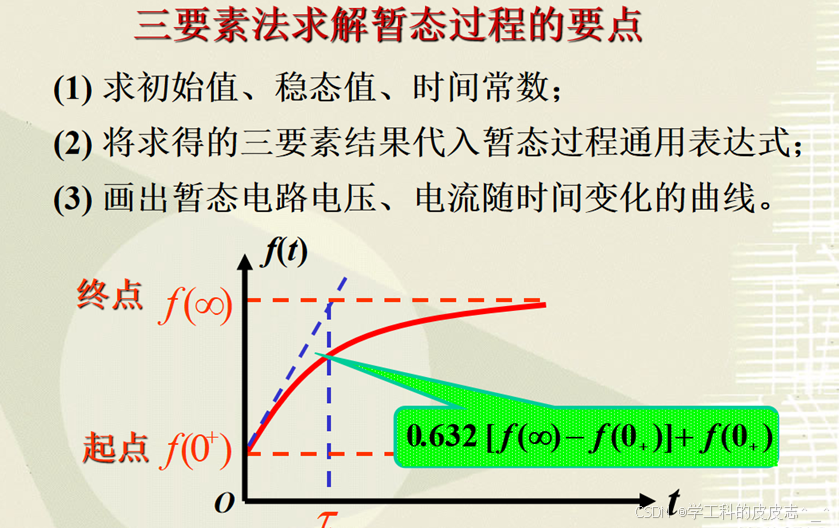
在这里插入图片描述

3.2.4 选取合适的时间常数

积分电路可以用来将矩形波变成锯齿波输出，成立的条件是时间常数RC>>tp，否则电压C将会出现电压饱和。
在这里插入图片描述
①　当τ过小时，电容很快就充电到与输入电压一致

图19
②　当逐渐增大τ值时
在这里插入图片描述
图20

图21

四、无源RC低通滤波器

这是无源RC低通滤波器的电路结构，如下图22所示，滤波器是利用频率响应实现信号选择的一种装置，它可以从输入信号中选出某些特定频率的信号作为输出。根据实现方式的不同，滤波器可以分为模拟滤波器和数字滤波器，低通滤波器就是指低频信号更容易通过的滤波电路。
在这里插入图片描述
图22

4.3.1 截止频率推导

在这里插入图片描述

 电压随电源频率变化的特性称为电压频率特性；
 电流随电源频率变化的特性称为电流频率特性，
 阻抗随电源频率变化的特性则称为阻抗频率特性。
因为电压、电流和入端阻抗都是频率的复函数，因此可以表示成模（幅值）和辐角（或相位）的形式，显然它们的模（幅值）和辐角（或相位）也都是频率的函数。它们的模（幅值）随频率变化的特性称为幅频特性，辐角（或相位）随频率变化的特性称为相频特性。
在这里插入图片描述

图23 无源RC低通滤波器的幅频特性和相频特性
幅值|H(ω)|等于最大值的0.707倍处的频率记为Wc。显然，Wc=1/RC,数值上等于该一阶RC电路的时间常数的倒数。工程技术中认为幅值大于0.707倍最大值时该滤波器就是导通的，否则就是截止的。因此，把角频率从0到Wc的范围称为低通函数的通频带，称为截止频率。时域分析中以时间常数RC表征过渡过程的快慢，而频域分析中以截止频率Wc=1/RC作为衡量其滤波性能的定量指标。

4.3.2 无源积分电路和无源滤波器的关系

无源积分电路和无源滤波器都是电路中常见的无源元件。它们的关系在于，无源积分电路是一种低通滤波器，它能够将高频信号滤除，并且能够对低频信号进行积分。因此，无源积分电路可以作为一种简单的低频滤波器来使用，积分电路常用于波形转换，如将矩形波变三角波。对正弦波积分可以实现相移。
与之相比，无源滤波器更加灵活，它可以是低通、高通、带通、带阻等类型的滤波器，可以对不同频率的信号进行滤波。无源滤波器的电路通常包括电容、电感和阻值元素，在不同频率下这些元素的组合可以实现不同类型的滤波器。
无源滤波器对信号有固定的衰减，仍需靠运放作增益补偿。

五、有源积分电路

5.4.1 最基本的有源积分电路

最基本的有源积分电路如图 24 所示
在运放的线性工作范围内，运放的反相输入端电位近似等于同相输入端电位，即近似为零电位。故流过电阻 R 的电流为 iR = Ui/R。这个电流应该近似等于流过电容的电流 iC 的负值，
即 iR =﹣iC。
电容的定义式为：
在这里插入图片描述

这就是积分电路的时域输入输出关系。式中 Uo(0)为输出电压的初始状态，即电容 C 的初始电压。由于表达式中存在一个负号，故该电路称为反相积分电路。
对于正弦稳态分析来说，电容 C 的容抗为：1/(jwC)。根据 iR =﹣iC，可以得到：

在这里插入图片描述
这就是积分电路的频域传递函数。表达式中的“j”表示输出正弦波相比于输入正弦波移相了+90°（即余弦波）。当然，在这个表达式中，要求输入 Ui 和输出 Uo 都是正弦波。

5.4.2 实际的有源积分电路

但是这个电路实际上是存在问题的。这个问题就是运放缺乏直流负反馈，这就使得运放无法工作在线性状态。、
因为运放的直流增益相当高（一般来说 100dB 是典型值），所以，只要运放的两个输入端存在哪怕极小的电位差，运放的输出电位就会超过线性区。而运放的两个输入端存在电位差是必然的。所以要想使运放工作在线性区，直流负反馈是必须的。为了解决这个问题，一般在电容 C 的两端并联一个电阻，以降低积分电路的直流增益，形成如图25 所示的电路。
在这里插入图片描述
图25 具有直流负反馈的积分电路

这个反馈电阻 Rf 的存在，对于用于将方波转换成三角波的积分电路而言，将会使得输出的三角波不再是线性的，而是成为一种指数型变化的波形；而对于用于对正弦波进行 90°移相的积分电路而言，则会使得 90°移相带来误差。
对于用于将方波转换成三角波的积分电路而言，引入反馈电阻 Rf 以后，反馈通道的电流就成为两个电流之和：一个是流过反馈电阻 Rf 的电流，另一个则是流过积分电容 C 的电流。显然，如果流过 Rf 的电流远远小于流过电容 C 的电流，则其影响就很小，以至于可以忽略不计。所以，
在这里插入图片描述
由于反馈电阻 Rf 的引入使得积分电路的表达式不再准确，所以，采用反相积分电路对正弦波进行 90°的移相就会存在必然的移相误差。所以，需要重新推导引入反馈电阻 Rf 以后的频域传递函数。
反馈电阻 Rf 显然与积分电容 C 构成了一个 RC 阻抗，设这个阻抗为 Z，如图 26 所示。从电路结构来看，完全可以将其看成一个反相比例放大器，为保证集成运放输入级差分放大电路的对称性，应在同相输入端加入一个电阻R ′应等于R的阻值。
在这里插入图片描述

5.4.3 有源积RC低通滤波器

根据下方式子，很容易看出这也是一个低通滤波器，从前面的系数我们可以知道是带增益的低通滤波器。
在这里插入图片描述

5.4.4 有源积分电路和有源滤波器异同点

积分电路常用于波形转换，如将矩形波变三角波。对正弦波积分可以实现相移。
有源积分电路和有源滤波电路都是基于运放（放大器）的电路，它们的主要功能是在信号处理过程中增加或减小特定频率的信号，同时抑制或增强其他频率的信号。虽然它们的功能有所相似，但是它们的设计和作用有一些重要的区别和异同点。
区别：
1.
功能不同：有源积分电路主要用于积分（对信号进行时间积分），而有源滤波电路主要用于滤波（对信号进行频率滤波），可以设计成低通，高通，带通，带阻。
2.
电路的反馈方式不同：有源积分电路采用电容的反馈方式，有源滤波电路可以采用电感或者电容的组合反馈方式。
3.
滤波效果不同：有源积分电路可以削弱高频信号，而有源滤波电路可以削弱或增强特定频率的信号。

异同点：
1.
都需要使用运放放大器实现。
2.
都需要电容元件来实现滤波或积分功能。
3.
都可以使用负反馈来实现稳定性。
4.
都需要选取合适的电阻、电容、电感等元件来满足特定的设计要求。
5.
都需要考虑运放的输入阻抗、输出阻抗、带宽等特性。
6.
总的来说，有源积分电路和有源滤波电路都是基于运放的电路，它们的功能和设计有所不同，但是都可以使用类似的元件和技术来实现。在实际应用中，需要根据具体的要求和信号特性来选择合适的电路。