硬件简单基础

容抗公式：XC=1/ωC=1/（2πfC） 感抗公式：XL = ωL = 2πfL
计算频率：f＝1/2πRC ；计算阻抗：x＝1/2πfC
谐振会引起空载电压小于带载电压（获得更大的电压电流），产生过电压。
电容的电压相位滞后电流90°；电感的电流相位滞后电压90°
详情可看： https://zhuanlan.zhihu.com/p/144174884
一、
1、电感（RL电路）
电感会防止电流的突变，使其变化平缓。电感越大，电流变化曲线越平缓。当电感充满电时，开关打向右侧，若电阻小于140，则会使电压大小变小，电流变化变缓（电阻小会减小电流的损耗）；若电阻大于140，电流变化剧烈（电阻大增大电流的损耗）


2、电容（RC电路）
电容会防止电压的突变，使电压变化平缓。电容越大，会使电压变化越小。电阻变大变小只会改变电流的大小，对电压变化无影响。


3、LRC电路
分为欠阻尼、过阻尼、零阻尼、临界阻尼这四个状态。会产生谐振，欠阻尼时，由于电阻的作用，会消耗能量，所以会衰减震荡（主要是依靠电阻的大小来控制），处于该状态时，电感给电容充电，直到电感的电流为0，此时电容的电压达到最大值，电容开始放电给电感充电，直到电容的电压为0，此时的电感的电流为最大，不断循环重复这个过程，逐渐衰减为0。
所谓的阻尼就是描述系统达到稳定时过程，当外界施加一个激励时，零阻尼时，系统在平衡状态上下来回振荡；过阻尼时，系统可以一次达到平衡状态，但是需要很长的时间，快速性不够；欠阻尼时，系统在平衡状态处来回振荡，最终达到平衡；临界阻尼时，系统快速准确的达到了平衡状态，这是我们理想的状态。
临界阻尼计算公式：R=2√(L/C) ，
过阻尼：R>2√(L/C)，此时电路有不等负实数的两个特征根，非振荡放电过程。
欠阻尼：R<2√(L/C)，此时电路有一对共轭复数的两个特征根，振荡放电过程。
零阻尼：R=2√(L/C)，此时电路有两个相同的特征根，处于非振荡放电的临界状态。
1、欠阻尼状态
当0<ζ <1时的解为一对实部为负的共轭复根，系统时间响应具有振荡特征，称为欠阻尼状态。
2、临界阻尼
当ζ = 1时的解为一对重实根，此时系统的阻尼形式称为临界阻尼。现实生活中，许多大楼内房间或卫生间的门上在装备自动关门的扭转弹簧的同时，都相应地装有阻尼铰链，使得门的阻尼接近临界阻尼，这样人们关门或门被风吹动时就不会造成太大的声响。
3、过阻尼
当ζ > 1时的解为一对互异实根，此时系统的阻尼形式称为过阻尼。当自动门上安装的阻尼铰链使门的阻尼达到过阻尼时，自动关门需要更长的时间。



4、串联谐振（产生谐振时电抗Xc+XL=0）
由于电感的电流滞后电压90°，电容的电流超前电压90°，所以其二者放电时产生的电流方向是相对的，又因为二者处于串联状态，所以二者的电流变得相位（方向）相同，所以产生的谐振会更大。（谐振是频率相同，相位相同的波形的叠加）
交变电源的频率越接近电容电感的频率产生的谐振越强（过电压）
串联谐振的谐振频率为:
可见以上计算谐振频率公式中不涉及电路中电阻的影响，其可以满足大多数的情况。但是，在低频情况下（使用具有相当大内部电阻的大型电感器）常常不够准确。在这种情况下，需要一个更复杂的公式，其中也要考虑电阻。以下公式可用于低频（较大的内部电阻）计算。

5、并联谐振
由于电感和电容相互并联，其二者放电时产生的电流方向相对，相互抵消（但也会有一定的电流溢出，阻碍电源电流）。当电源的频率接近电感和电容相互并联的频率时，相当于电感和电容相互完全抵消，电路中电感和电容并联的这一部分处于开路状态，此时产生的谐振最小。

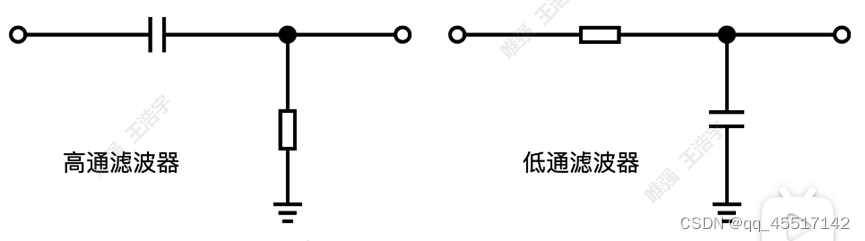
6、高通滤波器（RC）
实际看作电阻分压的原理，当频率无穷大的时候，电容容抗为0，A=输出/输入=1，即输出和输入波形一致；当频率较小的时候，电容的容抗大，由于电阻的分压原理，输出的波形与输入差别较大；当频率为0时，容抗无穷大，断路。
临界点的频率用公式f＝1/2πRC计算，大于该频率通过

7、低通滤波器(RC)
与高通滤波原理相似，都是利用电阻的分压原理。

8、高通滤波器(RL）
与RC电路原理相似，同样是电阻分压原理，感抗= XL = ωL = 2πfL。

9、低通滤波器(RL)
与RC电路原理相似，同样是电阻分压原理，感抗= XL = ωL = 2πfL。

10、带通滤波器
实质为高通滤波与低通率波的结合，使其输出的频率能够在一定的范围内。

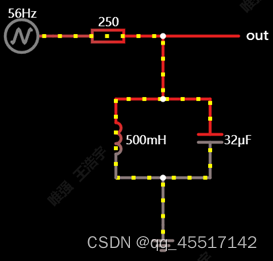
11、π型滤波电路
π型滤波器设计的经验在电子电力设计中
π滤波器的layout需要较宽的走线
将π滤波器与供电元件隔离开来尤为重要
输入电容，电感和输出电容的间距要小
输出电容的地线层需要直接与驱动电路相连
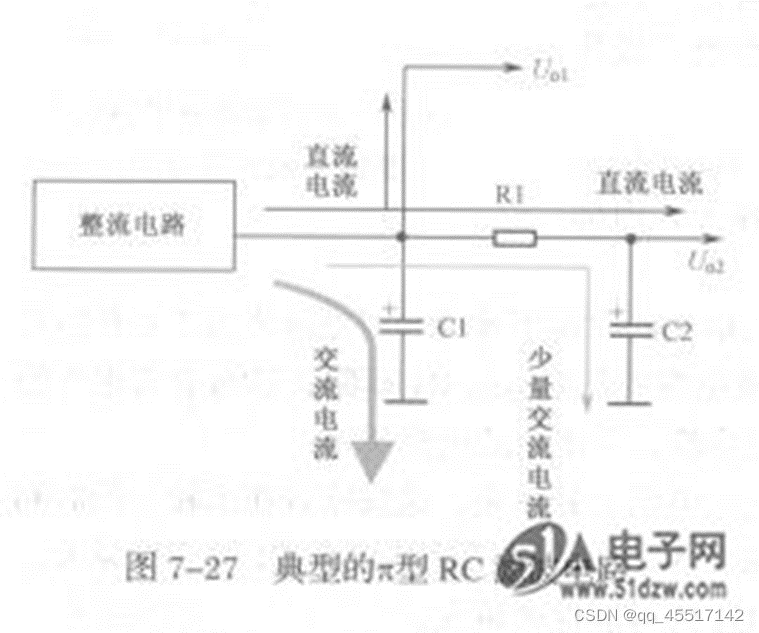
（1）π型RC滤波电路
图7-27所示是典型的π型RC滤波电路。电路中的C1、C2是两只滤波电容，R1是滤波电阻，C1、R1和C2构成一节π型RC滤波电路。由于这种滤波电路的形式如同字母π且采用了电阻、电容，所以称为π型RC滤波电路。
这一电路的滤波原理是：从整流电路输出的电压首先经过C1的滤波，将大部分的交流成分滤除，见图中的交流电流示意图。


（2）π型LC滤波电路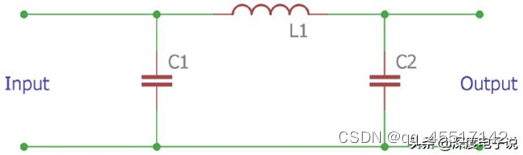
π型滤波器用于低通滤波，π滤波器是一种出色的低通滤波器，与传统的LC滤波器有很大不同。当π滤波器用于低通滤波时，输出稳定且K值固定。
因为这是一个低通滤波器，它在高频下产生高阻抗，在低频下产生低阻抗。因此，常用于传输线路中隔绝不必要的高频信号。
π滤波器中每个元件的值的计算可以由以下公式得出，方便你设计应用
截止频率fc=/1/ᴫ(LC)1/2
电容值 C=1/Z0 ᴫfc
电感值 L1=Z0/ ᴫfc
其中Z0为阻抗π型滤波器用于高通滤波

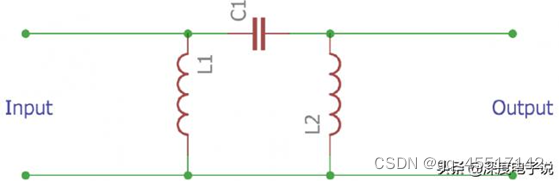
π滤波器同样可以被配置成高通滤波器。这种配置下，滤波器会隔绝低频信号，通过高频信号。而且同样由两种无源器件组成，两个电感和一个电容。
在该配置下，其参数计算参照以下公式。
截止频率 fc= 1/4ᴫ(LC)1/2
电容值 C=1/4Z0ᴫfc
阻抗值 L1=Z0/4ᴫfcπ型滤波器的优点高输出电压
π滤波器的输出电压很高，所以适用于需要高压直流滤波的应用。低纹波系数
若以低通滤波配置来进行直流滤波的话，π滤波器是一种效率很高的滤波器，可以从桥式整流器输出端滤除不必要的交流纹波。电容在交流下阻抗低，但在直流下阻抗高。
12、积分电路
输出端的电容接地，所以输出的高频信号会被短路。积分电路可以将输入的方波信号转换为锯齿波信号，主要是依靠电容的充放电特性。（在电容还没有完全充满电时即电压上升时，方波信号改变方向电压缓慢下降）

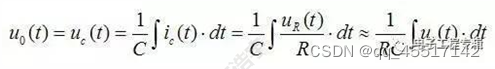
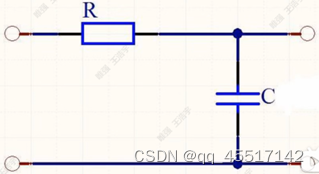
13、微分电路
电容C与电阻R的串联作为输入端，电阻R两端为输出端，即满足Uo=Ui-Ue，由于电路中有电容C和电阻R存在，故在外加电压的作用下，存在着的充、放电过程。当矩形脉冲输入端后，在输出端可得到一对正、负尖脉冲。（产生的尖脉冲，是因为在输入时的上升沿，电压变化很大，所以du/dt很大，所以ic很大，输出Uo=ic*R，所以Uo很大产生尖脉冲；在输入处于下降沿时同理）


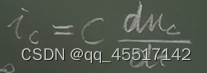
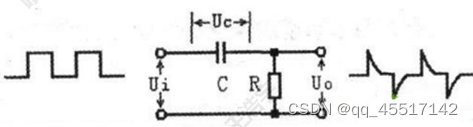
二、
1、截止频率
截止频率fc，用来描述一个滤波器或一个放大器频率特性的指标。一个滤波器或一个放大器，当保持输入信号的幅度不变，改变信号频率使输出信号降至最大值的0.707倍（对应-3dB），或0.5倍时（对应-6dB），该频率称为截止频率。 cut-off frequency
对于一个滤器器来说，在高频端和低频端各有一个截止频率，分别称为上截止频率fH和下截止频率fL。两个截止频率之间的频率范围称为通频带。 BW=fH-fL。

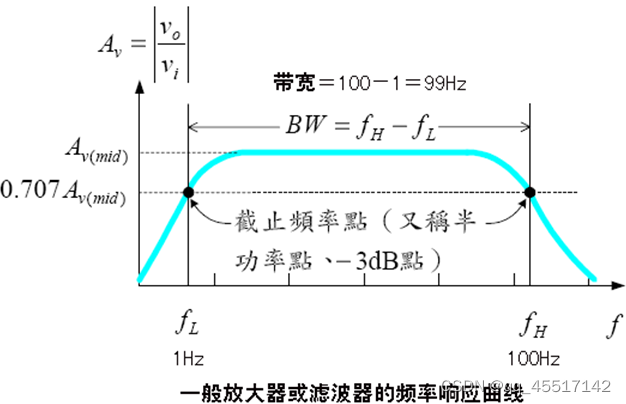
A若小于0.707（即频率小于截止频率）则信号衰减严重；A高于0.707（即频率大于截止频率）则信号得到加强。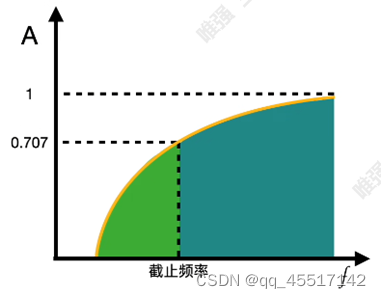
2、带负载能力
带负载能力就是代表器件的输出电流的大小。对于标准TTL器件，输出负载能力的高电平为0.4mA，而作为下级负载的TTL器件的输入高电平电流为0.04mA(40uA)，这样一个标准TTL器件最大可以驱动8个以上标准TTL负载。
所谓带负载能力，是说电路的输出电阻的大小，和电压源（电流源）中的内阻是一个意思。
带负载能力是指，外接器件后，输出的电压或电流大小不受影响的能力。比如，如果一个单片机的引脚输出5伏电压信号，如果接上一个负载后，它的5伏保持不变，那么，它就可以带动这个负载，如果变小，那就说明带不动负载。同样，如果输出的电流能够满足负载的需要，那就说明带负载能力满足要求，反之亦然。
若想要稳定的输出电压，则要求输出的电阻越小越好（相当于内阻 分压小）；若想要输出稳定的电流，则要求输出的电阻越大越好（相当于并联 分流小）。

3、单片机外围电路
其实质就是为了满足单片机芯片去完成一些特定的功能，而单独设计的电路模块，可以直接套用在单片机的对应引脚上。某一种芯片或者集成电路如果通电，无法正常工作，或者无法得到如愿的效果，需要添加一些别的电路完成集成电路的工作效果，可能一种集成电路，加上不同的外围电路，就会达到不同的效果。
具体内容可见：https://zhuanlan.zhihu.com/p/357376159
4、信号传输
（1）单端信号：
在数据传输的过程中，只有一条信号线进行数据的传输。在此情况下，在不同的地点，地面的电势不同，造成信号在不同地区与地面的电势差不一样，所受到的干扰更强，信号不稳定。

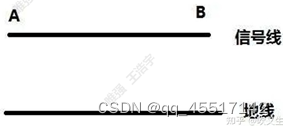
（2）差分信号：
在数据传输中，有两条信号线同时传输信号，两信号的大小相同，方向相反，我们所读取的信号是两个信号之间的差值，无论在什么样的干扰下，两信号的差值一直是不变的（有干扰信号时，两个信号同时增加或者减少，所以差值不变），所以信号比较稳定，抗干扰能力强。

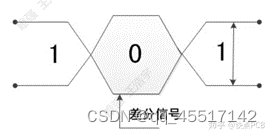
（3）共模信号与差模信号
在地与导线之间并联电容器，可以滤除波动的信号（共模信号）；共模信号滤除需要经过大地，差模滤除在两个信号线之间并电容
差模信号通过一对信号线来传输。一个信号线上传输我们通常所理解的信号；另一个信号线上则传输一个等值而方向相反的信号。差分和单端模式最初出现时差异不大，因为所有的信号都存在回路。
　　单端模式的信号通常经由一个零电压的电路来返回。差分信号中的每一个信号都要通过地电路来返回。由于每一个信号对实际上是等值而反向的，所以返回电路就简单地互相抵消了，因此在零电压或者是地电路上就不会出现差分信号返回的成分。
　　共模方式是指信号出现在一个(差分)信号线对的两个信号线上，或者是同时出现在单端信号线和地上。对这个概念的理解并不直观，因为很难想象如何产生这样的信号。这主要是因为通常我们并不生成共模信号的缘故。共模信号绝大多数都是根据假想情况在电路中产生或者由邻近的或外界的信号源耦合进来的噪声信号。共模信号几乎总是“有害的”，许多设计规则就是专为预防共模信号出现而设计的。

首先共模和差模这两个词可以说是一种位置概念的意思，图中的系统描述的是AB两个模块间通过1、2两根信号线传递信号，共模就是指1、2与GND的关系而差模指的是1和2之间的关系。简而言之，共模关注的是信号线与地线间的关系，而差模关注的是信号线间的关系。

共模信号和差模信号这两个概念多用于差分电路如（差分放大电路），还是以这个图为例，若1的电压为V1,2的电压为V2，则1和2的共模信号都为（V1+V2）/2，1的差模信号为（V1-V2）/2,2的差模信号为（V2-V1）/2，在这种概念的环境下，每根信号线兼具共模信号和差模信号两个参数，每个信号的共模信号与差模信号之和为该条信号线的总信号。（如V1=1的共模＋1的差模=（V1+V2）/2+（V1-V2）/2） 单独一根信号线没法谈共模差模，两根信号线才会有差模信号共模信号的说法，分别描述了这两根信号线电位与地线电位之差和这两根信号线电位之差。
共模干扰就是指两条信号线与地之间的干扰信号，差模干扰就是两条信号线间的干扰信号。来源一般有两种：
传导干扰：主要就是地线电位不稳定带来干扰，地线电位如果发生浮动，那地线与信号线间的电压就会不稳定也就是共模电压不稳定，即产生了共模干扰。若两根线上的共模干扰电压不一致，则还会使这两根信号线的差值发生浮动，引起差模干扰。我们常将信号线做成双绞线的原因就是让两根信号线的空间位置相对接近使它俩的共模干扰电压一致从而尽可能的消除了差模干扰，如果我们想得到的是信号线的差值，这样做就会大大减小误差。
空间耦合干扰：空间中变化的电磁场在信号线上产生压降带来共模和差模干扰。
（4）差分信号线的布线
通常差分信号也是高速信号，所以高速设计规则通常也都适用于差分信号的布线，特别是设计传输线1这样的信号线时更是如此。这就意味着我们必须非常谨慎地设计信号线的布线，以确保信号线的特征阻抗沿信号线各处连续并且保持一个常数。
在差分线对的布局布线过程中，我们希望差分线对中的两个PCB线完全一致。这就意味着，在实际应用中应该尽最大的努力来确保差分线对中的PCB线具有完全一样的阻抗并且布线的长度也完全一致。差分PCB线通常总是成对布线，而且它们之间的距离沿线对的方向在任意位置都保持为一个常数不变。通常情况下，差分线对的布局布线总是尽可能地靠近。（一个板子上不止一个差分线对）
（5）差分信号的优缺点
优点：
a、抗干扰能力强。干扰噪声一般会等值、 载到两根信号线上，而其差值为 0，即：噪声对信号的逻辑意义不产生影响。
b、能有效抑制电磁干扰（EMI）。由于两根线靠得很近且信号幅值相等，这两根线与地线之间的耦合电磁场的幅值也相等，同时他们的信号极性相反，其电磁场将相互抵消。因此对外界的电磁干扰也小。
c、时序定位准确。差分信号的接受端是两根线上的信号幅值之差发生正负跳变的点，作为判断逻辑 0/1 跳变的点。而普通单端信号以阈值电压作为信号逻辑 0/1 的跳变点，受阈值电压与信号幅值电压之比的影响较大，不适合低幅度的信号。
缺点：若电路板的面积非常紧张，单端信号可以只有一根信号线，地线走地平面，而差分信号一定要走两根等长、等宽、紧密靠近、且在同一层面的线。这样的情况常常发生在芯片的管脚间距很小，以至于只能穿过一根走线的情况下。
5、电气特性：电气特性是指每一根信号线上的信号方向及表示信号有效的电平范围，通常，由主设备（如CPU）发出的信号称为输出信号（OUT），送入主设备的信号称为输入信号（IN）。
6、0Ω电阻的作用
（1）在电路中没有任何功能，只是在PCB上为了调试方便或兼容设计等原因。
（2）可以做跳线用，如果某段线路不用，直接不贴该电阻即可(不影响外观)
（3）在匹配电路参数不确定的时候，以0欧姆代替，实际调试的时候，确定参数，再以具体数值的元件代替。
（4）想测某部分电路的耗电流的时候，可以去掉0ohm电阻，接上电流表，这样方便测耗电流。
（5）在布线时，如果实在布不过去了，也可以加一个0欧的电阻。
（6）在高频信号下，充当电感或电容。(与外部电路特性有关)电感用，主要是解决EMC问题。如地与地，电源和IC Pin间。
（7）单点接地(指保护接地、工作接地、直流接地在设备上相互分开，各自成为独立系统。)
（8）熔丝作用
（9）拟地和数字地单点接地
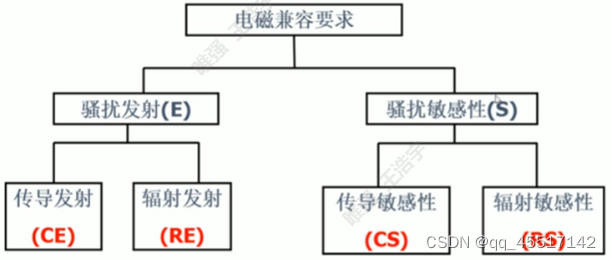
7、EMC电磁兼容
电磁兼容所下的定义为“设备或系统在其电磁环境中能正常工作且不对该环境中任何事物构成不能承受的电磁骚扰的能力”，即电子、电气设备或系统在同一电磁环境中能良好执行各自功能的这样一个共存状态，简单点说，就是各种设备都能正常工作又互不干扰，达到“兼容”状态。要注意电磁兼容所要求的两个基本方面：在共同的电磁环境中，不受干扰且不干扰其他设备。
EMC（电磁兼容）=EMI（电磁干扰）+EMS（电磁抗扰度）

8、驱动能力
（1）、问：为什么说驱动能力不够是因为提供电流太小而不是电压？和分析驱动能力不够？

答：首先我们看到的驱动能力不够大部分是在你选择的负载（电阻、喇叭等）电压符合供电电压的。那么电压符合了只有看电流大小是否足够。是电压还是电流引起驱动能力不够，给你个判断方法，将后级电流开路测试电压是否符合负载电压。符合但接上负载后电压就会降低这个就是电流驱动能力不够。如果电压不够则是驱动电压不够。

（2）、什么情况下要考虑启动能力驱动能力？

答： 任何情况都要考虑包括数字信号处理的接口电路里。但是长说的驱动能力都是在功率驱动的情况下用的比较多。

（3）、怎么知道在集成电路里和平常IC驱动能力是否足够？和提高驱动能力的办法

答： 在IC的资料里都有说明I/O口的驱动能力，根据你的负载所需要的驱动能力来判断这个I/C的I/O口是否符合如果不符合可以用三极管或者MOS管子放大提高驱动能力。

（4）、举例子：用一个IC驱动1个LED。IC输出电压5V，输出电流20mA。用来驱动一个白色LED。LED是20MA 3.3V的。

答： 那么5-3.3=1.7V 20MA时 1.7/20MA=85R。这样我们可以在LED上串接一个电阻85R的正接I/O负对地就可以了。 现在该为驱动300MA的3.3V的1WLED。I/O驱动能力就不够了需要提高驱动能力。分析输出5V输出20MA用三极管8050放大为200倍三极管集电极电流要在300MA计算得：300MA/200MA=1.5MA基极电流为1.5MA为了使三极管深度饱和选用10倍饱和电流。1.5*10=15MA 5V/15MA=333R则选用330R的电阻加到三极管基极和I/O口上发射极对地集电极接LED- LED+接电阻（5-3.3=1.7/0.33=5.1R）5.1R/1W。接+5V就可以了。
9、带负载能力
带负载能力是指，外接负载器件后，输出的电压或者电流不受影响的能力。比如，如果一个单片机的引脚输出5V的电压信号，如果接上一个负载后，它的5V保持不变，那么，它可以带动这个负载，如果变小，那就说明无法带动这个负载。同样，对于输出电流如果能够满足负载的需要，那就说明带负载能力满足要求。
10、光耦
光耦可以起到电气隔离的作用。当发光二极管导通后，会使三极管的基极也同样导通，从而可以使三极管导通。

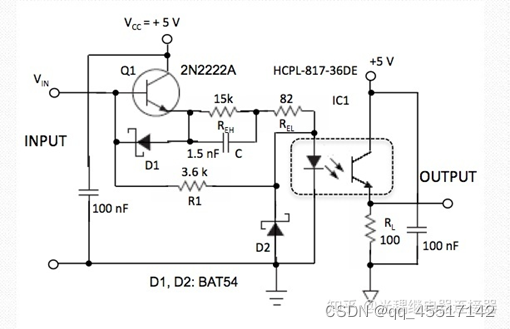
光耦分类：一种为非线性光耦，另一种为线性光耦。非线性光耦的电流传输特性曲线是非线性的，这类光耦适合于开关信号的传输，不适合于传输模拟量。常用的4N系列光耦属于非线性光耦。
线性光耦的电流传输特性曲线接近直线，并且小信号时性能较好，能以线性特性进行隔离控制。
由于光电耦合器的品种和类型非常多，在光电子DATA手册中，其型号超过上千种，通常可以按以下方法进行分类：
⑴按光路径分，可分为外光路光电耦合器（又称光电断续检测器）和内光路光电耦合器。外光路光电耦合器又分为透过型和反射型光电耦合器。
⑵按输出形式分，可分为：
a、光敏器件输出型，其中包括光敏二极管输出型，光敏三极管输出型，光电池输出型，光可控硅输出型等。
b、NPN三极管输出型，其中包括交流输入型，直流输入型，互补输出型等。
c、达林顿三极管输出型，其中包括交流输入型，直流输入型。
d、逻辑门电路输出型，其中包括门电路输出型，施密特触发输出型，三态门电路输出型等。
e、低导通输出型（输出低电平毫伏数量级）。
f、光开关输出型（导通电阻小于10Ω）。
g、功率输出型（IGBT/MOSFET等输出）。
h， 光敏电阻型（通过光，控制输出电阻，输出电阻可以双向，可以交流，改变了PC817之类只能一个方向的不便，纯电阻材料，无极性输出

11、温度漂移与零点漂移
放大电路在输入端短路（即没有输入信号输入时）用灵敏的直流表测量输出端，也会有变化缓慢的输出电压产生，称为零点漂移现象。
由温度变化所引起的半导体器件参数的变化是产生零点漂移现象的主要原因，因此也称零点漂移为温度漂移，简称温漂。温度漂移指环境温度变化时会引起晶体管参数的变化，这样会造成静态工作点的不稳定，使电路动态参数不稳定，甚至使电路无法正常工作。
温度升高，晶体管的电流放大倍数增大，Q点升高；反之减小。这部分额外增加的电流是温度变化引起的，理解为温度漂移。
零点漂移的信号会在各级放大的电路间传递，经过多级放大后，在输出端成为较大的信号，如果有用信号较弱，存在零点漂移现象的直接耦合放大电路中，漂移电压和有效信号电压混杂被逐级放大，当漂移电压大小可以和有效信号电压相比时，很难在输出端分辨出有效信号的电压。
在漂移现象严重的情况下，会使有效信号“淹没”，使放大电路不能正常工作。
12、运算放大器
正反馈：与原变化信号相同，被控部分发出的反馈信息促进和强化了被控部分的活动，最终使被控部分的活动与原来的活动方向一致。正反馈起加强控制信息的作用；使输出起到与输入相似的作用，使系统偏差不断增大，使系统振荡，可以放大控制作用。
负反馈：受控部分发出的反馈信息调整控制部分的活动，最终使受控部分的活动朝着与它原先活动相反的方向改变；反馈又指将系统的输出返回到输入端并以某种方式改变输入，进而影响系统功能的过程。负反馈起纠正、减弱控制信息的作用；使输出起到与输入相反的作用，使系统输出与系统目标的误差减小，系统趋于稳定。
A是增益，一般非常大（在坐标原点附近）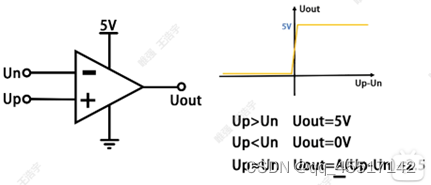
（1）电压跟随器


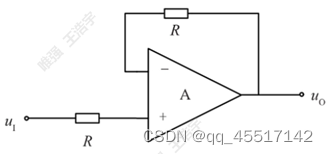
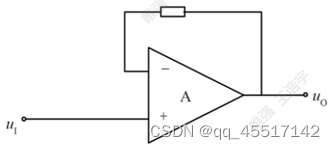
与同相比例放大器一个原理。输出端直接接到运放的负端就是跟随器，桥上加了电阻起保护作用，防止运放被击穿。（10k或20k）
主要起缓冲作用、隔离作用，提高带载能力作用。阻抗匹配问题。
输入阻抗大，输出阻抗小，连接前后两级阻抗不匹配的电路。
（2）同相运算放大器(反相端最终接地)
由可判断出其为负反馈电路，其判断过程：假设Vin为+→Vout为+→V1为+→Vin为-
因为Vin反馈回来的信号与原信号相反，所以为负反馈。


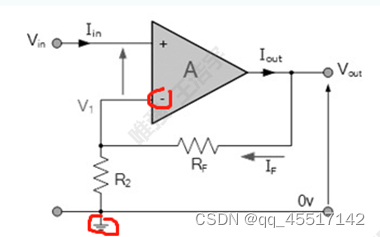
由此可见，同相运算放大器的增益A为正，所以输入与输出为同相的。
（3）反相运算放大器（同相端最终接地）
与以上分析相同，该电路为正反馈电路。


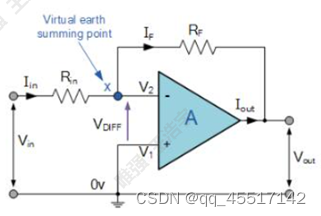
由此可见，反相运算放大器的增益为负，所以输入与输出反相。
13、电容：
电容频率特性：
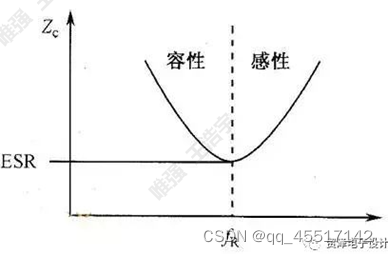
电容器在谐振频率以下表现为容性；在谐振频率以上时表现为感性，此时的电容器的去耦作用逐渐减弱。同时还发现，电容器的等效阻抗随着频率的增大先减小后增大，等效阻抗最小值为发生在串联谐振频率处的ESR（等效串联阻抗）。
串联谐振的谐振频率为: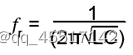
可见以上计算谐振频率公式中不涉及电路中电阻的影响，其可以满足大多数的情况。但是，在低频情况下（使用具有相当大内部电阻的大型电感器）常常不够准确。在这种情况下，需要一个更复杂的公式，其中也要考虑电阻。以下公式可用于低频（较大的内部电阻）计算。


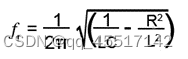
容值大小和ESL值的变化都会影响电容器的谐振频率由于电容在谐振点的阻抗最低，所以设计时尽量选用fR和实际工作频率相近的电容。在工作频率变化范围很大的环境中，可以同时考虑一些fR较小的大电容与fR较大的小电容混合使用。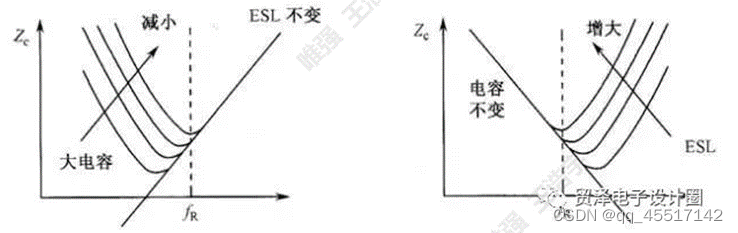
在频率较高的时候，电容的引线电感不能忽略，尤其是大容量电容，电感更大，电感和电容是串联的，在谐振频率以下，表现为容性，在谐振频率以上就表现为感性了，这时由于感抗已经超过容抗了。这种情况的电容已经表现为电感特性了。
（1）滤波作用：在电源电路中，整流电路将交流变成脉动的直流，而在整流电路之后接入一个较大容量的电解电容，利用其充放电特性，使整流后的脉动直流电压变成相对比较稳定的直流电压。频率高的交流电能够通过电容。
滤波作用是改变输出电压的波形，使波动比较大的电压变得更加平缓。
例如：原本电压波形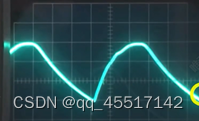
滤波后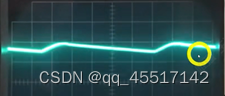
可见电压变得平缓

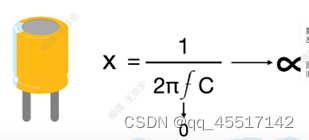
容抗计算公式（相当于电阻）

（2）耦合作用：两个或两个以上的电路构成一个网络时，若其中某一电路中电流或电压发生变化，能影响到其他电路也发生类似的变化，这种网络叫做耦合电路。耦合的作用就是把某一电路的能量输送（或转换）到其他的电路中去。（电容的隔直通交就是耦合，交流会产必变化的电场，从而产生电流）
在低频信号的传递与放大过程中，为防止前后两级电路的静态工作点相互影响，常采用电容藕合。为了防止信号中低频分量损失过大，一般总采用容量较大的电解电容。耦合包括直流耦合与交流耦合，
直流耦合 (DC Coupling)就是直流、交流一起过，并不是去掉了交流分量。
交流耦合 (AC Coupling)就是通过隔直电容耦合，去掉了直流分量。
比如在3V的直流电平上叠加一个1Vpp的弦波，如果用直流耦合，看到的是以3V为基准，+/-0.5V的正弦波；如果用交流耦合，看到的是以0V为基准，+/-0.5V的正弦波。
（3）降压作用：利用电容的容抗来降压，这在充电器中使用得很普遍；（电容损耗的是无功功率，产生的热量很小）
（4）隔直流作用：所谓隔离直流，其实就是高通滤波器的功能。这里的高通，指的是高频信号能通过，而低频信号较难通过，直流完全通不过；
（5）储能作用：电容有储能的作用，在使用电容储能时一般用大电容或者若干的小电容并联组成的电容组；
（6）旁路作用：旁路的主要功能就是产生一个电流分路，使较高频率的信号很容易通过此电容被旁路掉，低频的信号由于电容对它的阻抗较大而被输送到下一级放大；
旁路电容一般放在离芯片近的地方，这样受的干扰小，而且电容越小，滤除高频的能力越强。
（7）谐振作用：一般有电容的并联谐振和串联谐振，还可以通过谐振电容的串并联组合成陷波器等工程应用的滤波器。
（8）X电容与Y电容
X电容与Y电容也称为安规电容。没有正负极之分。
安规电容之所以称之为安规，它是指用于这样的场合：即电容器失效后，不会导致电击，也不危及人身安全。安规电容包含X电容和Y电容两种，它普通电容不一样的是，普通电容即使在外部电源断开之后，它内部储存电荷依然会保留很长一段时间，但是安规电容不会出现这个问题。安规电容大多数为蓝色、黄色、灰色以及红色等。
X电容用于滤除差模干扰，通过的信号相位相差180°，幅度没有变化，而电容只有两端存在电位差的时候才会工作，所以X电容可以滤除差模干扰。

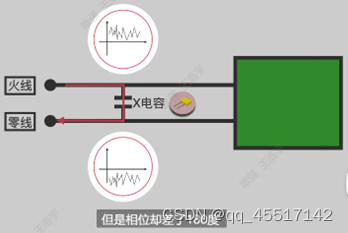
Y电容用于滤除共模干扰，通过的两条信号线同时受到幅值和相位相同的干扰，可以将产生的杂波通过Y电容滤除到大地。

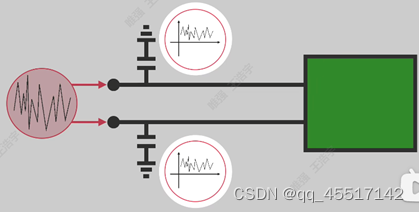
（9）铝电解电容
有正负极之分，主要用在给电源滤波，使波形更加平滑。耐压高，不可持续工作在高温状态，体积较大

（10）钽电容：属于电解电容，有正负极之分，用于电源滤波，可以持续工作在高温的状态下，体积小，价格贵。耐压小
（11）薄膜电容：中间的填充物为塑料，无正负极之分。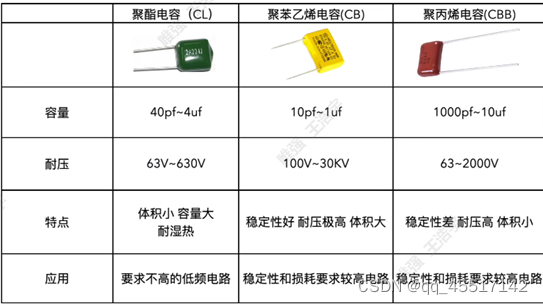
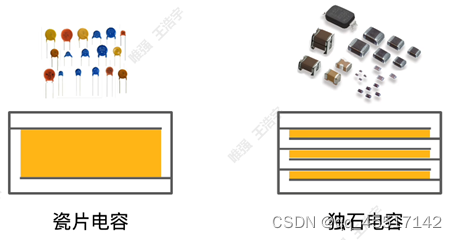
（12）陶瓷电容：分为瓷片电容和独石电容，陶瓷的介电常数非常高。瓷片电容的容量比较小，但是耐压比较高；而独石电容的容量比较大，但是耐压比较小。


14、运算放大器
（1）自激振荡
定义：自激振荡是指不外加激励信号而自行产生的恒稳和持续的振荡。如果在放大器的输入端不加输入信号，输出端仍有一定的幅值和频率的输出信号，这种现象就是自激震荡。（起振信号：电源上电产生的微小信号）

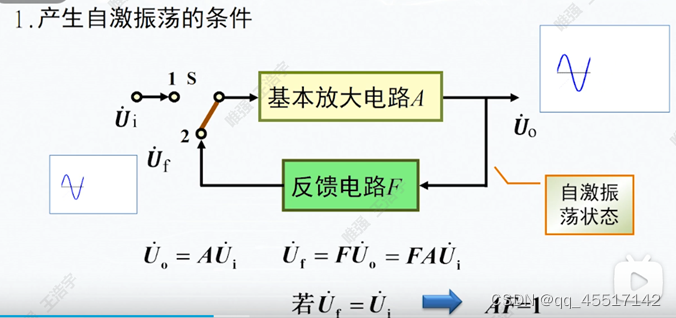
当电源上电时，给电路一个很小的起振信号Ui电路经过放大电路发达A，得到Uo=AUi，此时经过反馈电路放大F，得到Uf=FUo=FAUi，若Uf=Ui（即A*F=1），则此时不需要输入信号便可以产生一个稳定的振荡，这就是自激振荡。
（2）反馈
正反馈：反馈回来的信号和输入信号同相，对原信号起增强作用。
负反馈：反馈回来的信号和输入信号反相，对原信号起抑制作用。用于修正偏差
15. 模拟地与数字地
模拟信号是连续的，数字信号是间断的。数字信号与模拟信号要分别接不同的地，因为数字信号和模拟信号在相同的电流下输入的电压不同（一个连续，一个间断）。
15.电源转换电路设计