【无标题】π3：可扩展的Permutation-Equivariant（置换等变）视觉几何学习

---

---

标题：π3: Scalable Permutation-Equivariant Visual Geometry Learning
来源：上海AI Lab；浙大
主页：https://yyfz.github.io/pi3/

摘要

  $\pi 3$ 是一种前馈神经网络，为视觉几何重建提供了全新解决方案，彻底打破了对传统固定参考视角的依赖。以往方法常将重建结果锚定在特定视角，这种归纳偏差若参考点不理想，可能导致系统不稳定甚至失效。与之不同，$\pi 3$采用全置换等变架构，无需任何参考帧即可预测仿射不变的相机位姿和尺度不变的局部点云图。该设计使模型天然具备输入顺序鲁棒性和高度可扩展性。凭借这些优势，我们提出的简单无偏方法在相机位姿估计、单目/视频深度估计及密集点云图重建等广泛任务中均取得业界领先表现。

π3：可扩展的置换不变视觉几何模型

一、引言

  视觉几何重建作为计算机视觉领域长期存在的基础性课题，在增强现实[7]、机器人技术[50]和自主导航[17]等应用中展现出巨大潜力。传统方法主要采用束调整（BA）[11]等迭代优化技术应对这一挑战，而近年来前馈神经网络技术的突破性进展为该领域注入了新活力。DUSt3R [39]及其后续版本等端到端模型，已充分证明深度学习在图像对重建（如图像-视频配对）[13,46]、视频分析或多视角数据集重构（如多视图集合）[34,42,47]等场景中的强大能力。

  对单一固定参考视图的选择依赖。这种选定视图的相机坐标系被视为全局参考系，这一做法源自传统的运动恢复结构（SfM）[4,11,20,24]或多视图立体（MVS）[9,25]技术。我们认为这种设计选择引入了不必要的归纳偏见，从根本上制约了前馈神经网络的性能和鲁棒性。实证研究表明，这种对任意参考视图的依赖使得现有方法（包括最先进的VGGT[34]）对初始视图选择极为敏感。错误选择可能导致重建质量急剧下降，阻碍稳健且可扩展系统的开发（图3）。

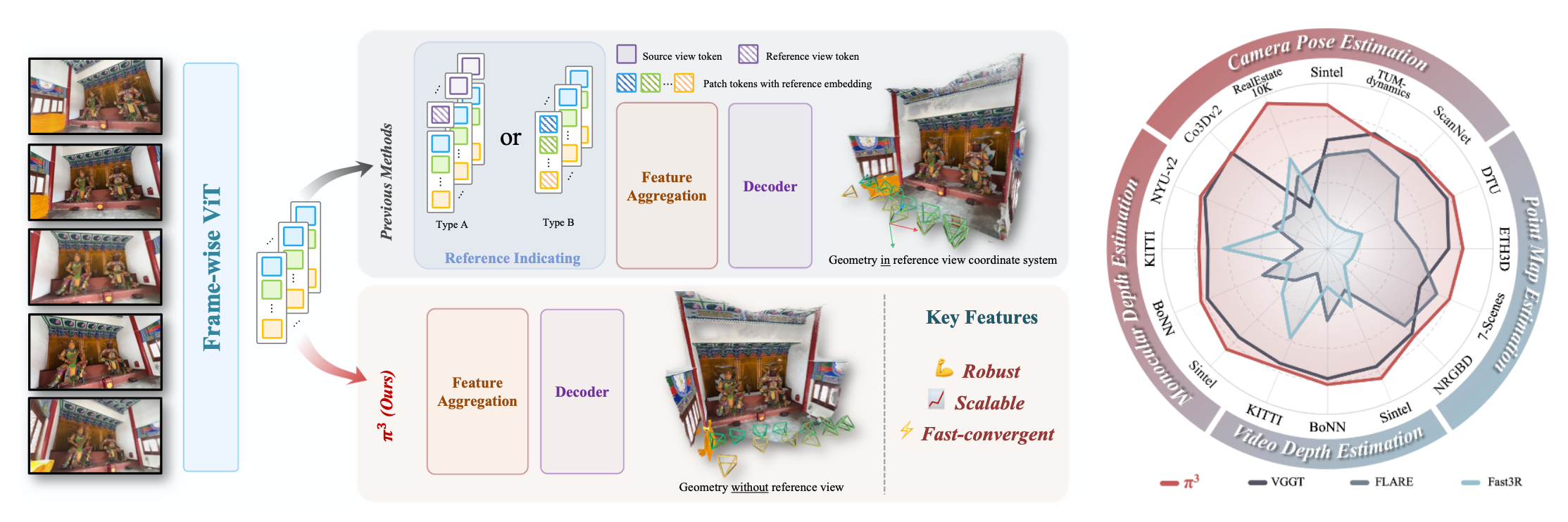
  π3能有效消除视觉几何学习中的参考视图偏差，支持多种输入形式：无论是静态场景的单张图像、视频序列，还是动态场景中的无序图像集，都不需要指定参考视图。我们的模型通过预测每帧图像的仿射不变相机位姿和尺度不变局部点云，所有参数均基于该帧自身的相机坐标系。摒弃依赖frame index的组件（如位置嵌入），并交替使用视图自注意力和全局自注意力的Transformer（类似[34]模型），π3实现了真正的permutation equivariance。这种设计确保了iamge与重建几何之间的稳定一对一映射。

  优势：可扩展性：随着模型规模的增加，性能持续提升（图2和图9）。其次，它实现了更快的训练收敛速度（图2和图9）。更强的鲁棒性：参考帧发生变化时，其性能下降幅度极小且标准差较低（图3和表4.5)。

  通过实验测试，π3，在单目深度估计方面，其性能可与MoGe [37]等现有方法相媲美；在视频深度估计和相机位姿估计方面，则超越了VGGT [34]。在Sintel基准测试中，π3将相机位姿估计的ATE值从VGGT的0.167降至0.074，并将尺度对齐视频深度绝对相对误差从0.299改善至0.233。此外，π3不仅轻量化且运行速度快，其推理速度达到57.4帧/秒，远超DUSt3R的1.25帧/秒和VGGT的43.2帧/秒。该算法能够重建静态和动态场景的能力

二、Permutation-Equivariant 框架

  Permutation-Equivariant 网络 $\varphi$，输入是N张图像序列，$S=(I_1,...,I_n)$，网络映射为输出tuple：

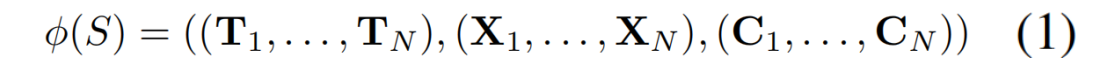
$T_i\in SE(3)\subset R^{4\times 4}$表示相机位姿，$X_i\in R^{H\times W\times 3}$是在相机坐标系中表示的像素对齐三维点图，$C_i\in R^{H\times W}$则是$X_i$的置信度图。

  对于任意Permutation $\pi$，设$P_{\pi }$为一个可置换序列顺序的算子。网络$\varphi$具有置换等变性质:

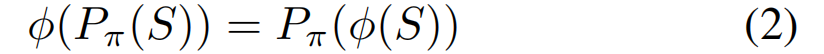
这意味着，对输入序列进行置换$(P_{\pi }(S)=I_{\pi }(1),...,I_{\pi }(N))$后，输出元组也会发生相同置换：

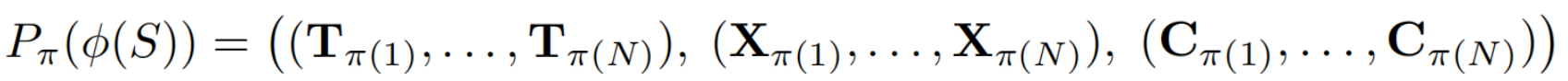
该架构确保每个图像与其对应输出之间保持一对一的稳定对应关系。这种设计具有三大核心优势：首先，重建质量不再受参考视图选择的影响；其次，模型对存在不确定性或噪声的观测数据展现出更强的鲁棒性；最后，该架构具有卓越的扩展能力。

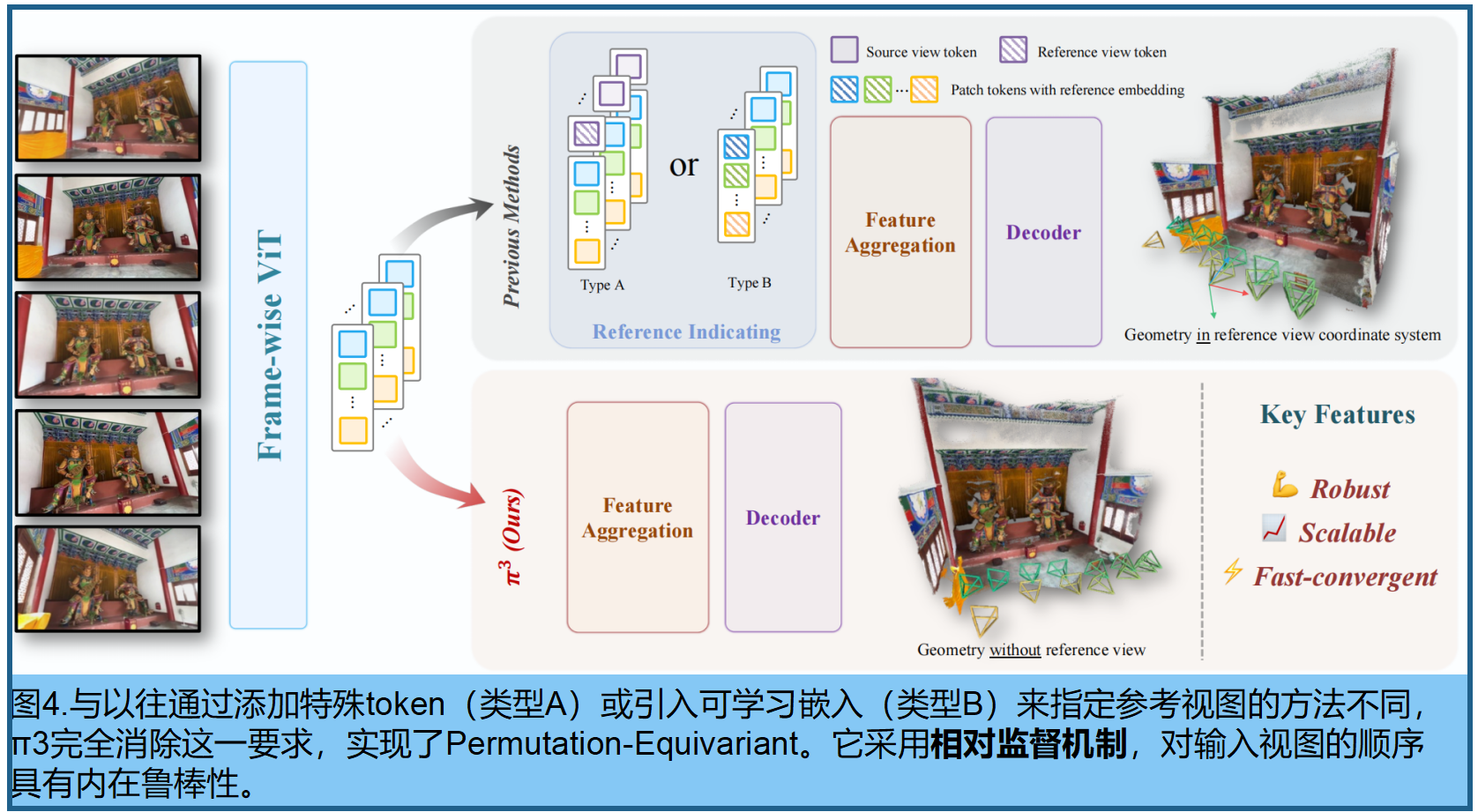
  具有等变性的π3方案如图4，完全省略了所有依赖顺序的组件（例如用于区分不同帧的位置嵌入，以及VGGT [34]中的指定参考视图的可学习token。流程首先通过DINOv2 网络将每个视图嵌入到一系列patch tokens 中，随后经过一系列交替的视图自注意力层和全局自注意力层处理，最终由解码器生成输出结果。

三、尺度不变的局部几何

  每张输入图像$I_i$，网络会预测像素对齐的三维点云图${\hat{X}}_i$。每个点云最初都定义在其自身的局部相机坐标系中。单目重建领域存在一个众所周知的挑战——固有的尺度模糊性。为解决这一问题，网络会在同一场景的N张图像中，预测出具有未知但具有一致性的缩放因子的点云$\hat{s}$。通过求解单一最优尺度因子$\hat{s}$，最小化预测点图$({\hat{X}}_i,...,{\hat{X}}_N)$与配准的对应真值$(X_1,...,X_N)$的深度加权的L1距离：

该问题通过采用[Moge: Unlocking accurate monocular geometry estimation for open-domain images with optimal training supervision]提出的ROE求解器进行求解。

  点云重建损失$L_{points}$：

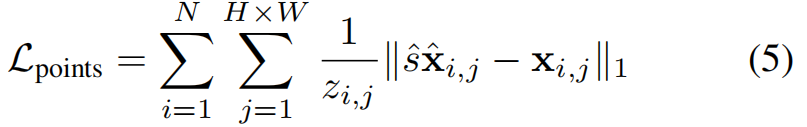
  为促进局部光滑曲面的重建，法向损失函数$L_{normal}$：对于预测点图${\hat{X}}_i$的每个点，其法向量$n_{i,j}$通过计算图像网格上相邻点向量的叉积获得。随后最小化其法向量与真实对应值之间的夹角来监督：

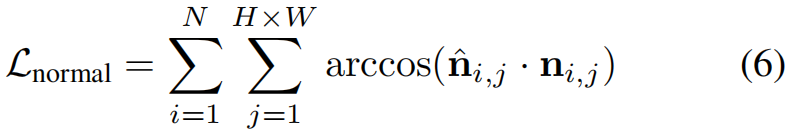
使用二元交叉熵（BCE）损失函数$L_{conf}$来监督预测置信图 $C_i$：对于每个点，若其L1重建误差 $\frac{1}{z_{i,j}}\Vert \hat{s}{\hat{X}}_{i,j}-X_{i,j}{\Vert }_1$低于阈值$ϵ$，则将其真实目标设为1；否则设为0。

  

四、仿射不变的相机位姿

  该模型的置换等变性，结合多视图重建固有的尺度模糊性，意味着输出的相机位姿（${\hat{T}}_1,...,{\hat{T}}_N$）仅在任意相似变换下具有唯一定义。这种特定类型的仿射变换由刚性变换和一个未知的全局尺度因子组成。

  为解决全局参考系的模糊性问题，我们通过监督网络对视图间的相对位姿进行训练。从视图 $j$ 到视图 $i$ 的预测相对位姿${\hat{T}}_{i\leftarrow j}$计算公式如下：

  每个预测的相对位姿${\hat{T}}_{i\leftarrow j}$由旋转矩阵${\hat{R}}_{i\leftarrow j}\in SO(3)$和平移矩阵${\hat{t}}_{i\leftarrow j}\in R^3$构成。虽然相对旋转对这种全局变换具有不变性，但相对平移的幅度存在不确定性，我们采用上一章得到的最优缩放因子 $\hat{s}$ 来解决这一问题。这个统一的缩放因子被用于校正所有预测相机的平移参数，从而让我们能够直接监督旋转参数和正确缩放后的平移分量。

   相机损失$L_{cam}$ ：旋转损失和位移损失的加权和，在所有有序视图对（i≠j）上取平均值：

旋转损失最小化 geodesic distance测地距离（角度）：

该迹反映了两个旋转矩阵的相似性。若两者完全一致，乘积为单位矩阵，迹为 3。以上损失来源于旋转矩阵 $R$ 的迹与旋转角度 $\theta$ 的关系：$Tr(R)=1+2cos\theta$。

平移损失采用Huber损失，因其对异常值具有鲁棒性：

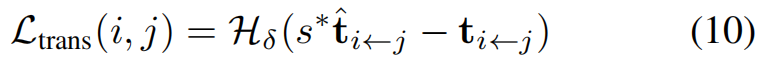
  我们的仿射不变相机模型 （假设局部区域的成像过程满足仿射变换，适用于远距离或弱透视、以及局部平面假设场景）建立在一个关键的见解之上：现实世界的相机路径具有高度结构化，而非随机。它们通常位于低维流形上——例如，环绕物体的相机沿球体移动，而车载相机则沿着曲线运动。

  图5定量分析了预测位姿分布的结构。特征值分析证实，与VGGT相比，我们预测位姿的方差，显著集中在更少的主成分上。这验证了输出结果的低维特性。关于这一现象的深入讨论，请参见附录A.3。

训练数据：15个多样化数据集，覆盖了室内外环境，从合成渲染到真实场景捕捉的各类场景。具体数据集包括：GTASfM [35]、CO3D [21]、WildRGB-D [41]、Habitat [23]、ARKitScenes [2]、TartanAir [40]、ScanNet [5]、ScanNet++ [44]、BlendedMVG [43]、MatrixCity [15]、MegaDepth [16]、Hypersim [22]、Taskonomy [45]、Mid-Air [8]等。

五、实验

  在四个任务中评估了π3：

5.1 相机位姿估计

  Angular Accuracy Metrics（角度测量指标）：基于[VGGT,Dust3R]，在场景级RealEstate10K [49]和以物体为中心的Co3Dv2 [21]数据集上评估相机位姿预测（超1000个测试序列），逐序列随机抽10张图像，形成所有可能的配对组合，并计算相对旋转和平移向量的角度误差。见表1

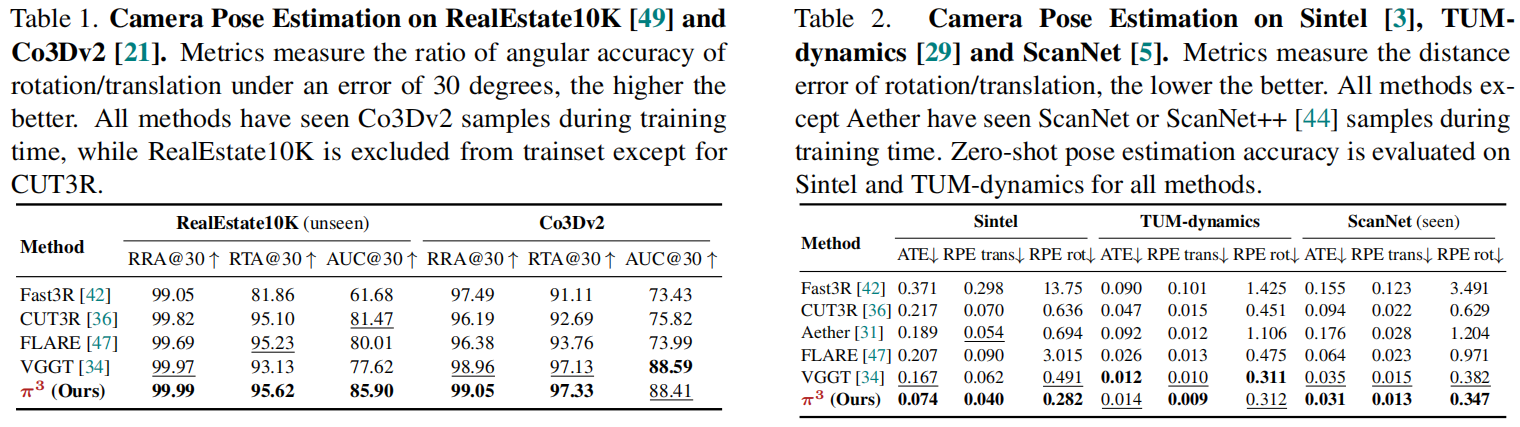
  Distance Error Metrics（距离误差指标）。根据VGGT，在合成的Sintel [3]户外数据集以及真实场景的TUM-dynamics [29]和ScanNet [5]室内数据集上，报告绝对轨迹误差（ATE）、平移相对位姿误差（RPE trans）和旋转相对位姿误差（RPE rot）。在计算误差前，我们通过Sim(3)变换将预测的相机轨迹与真实值进行对齐。见表2

  

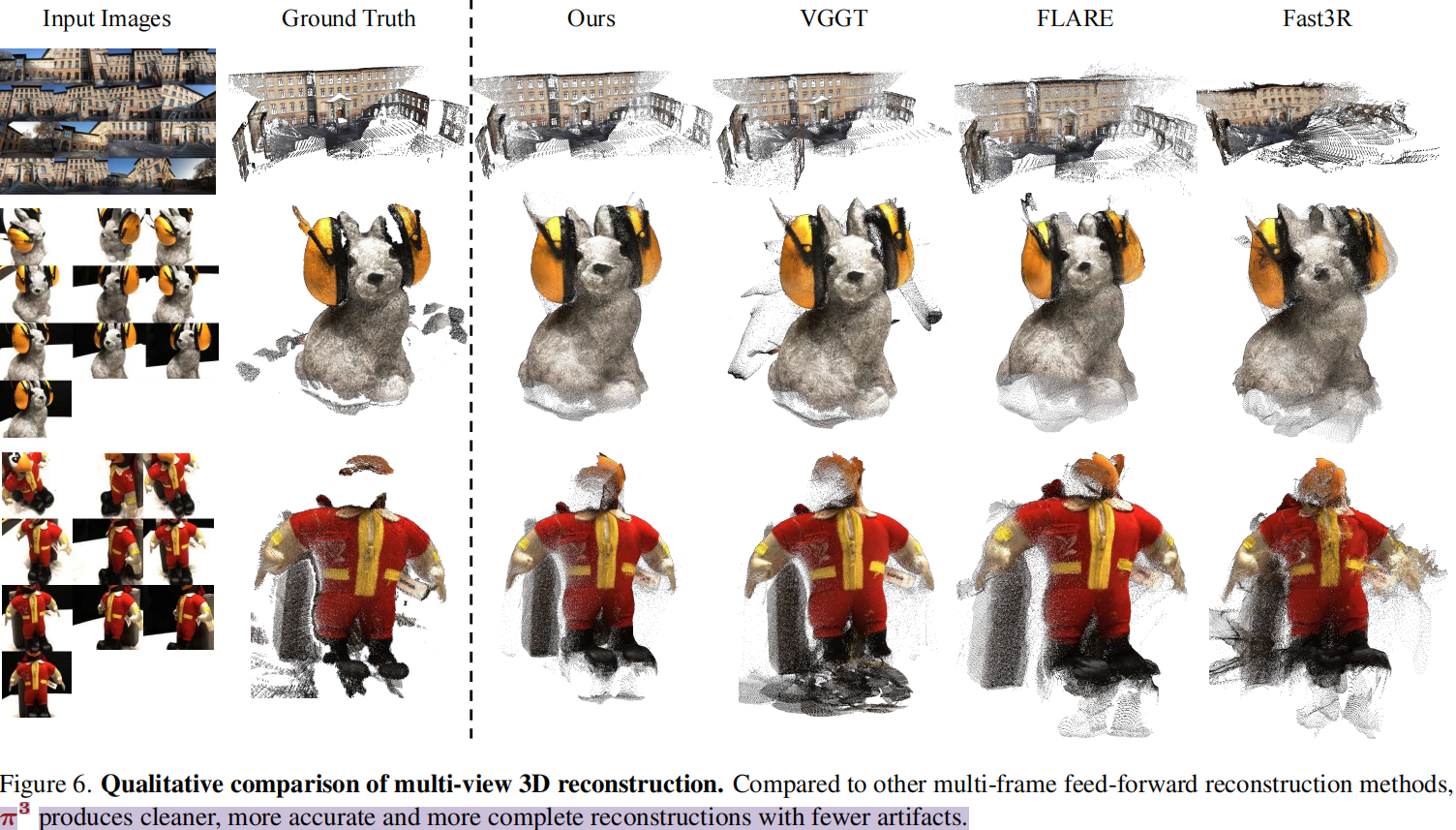
5.2 点云图估计

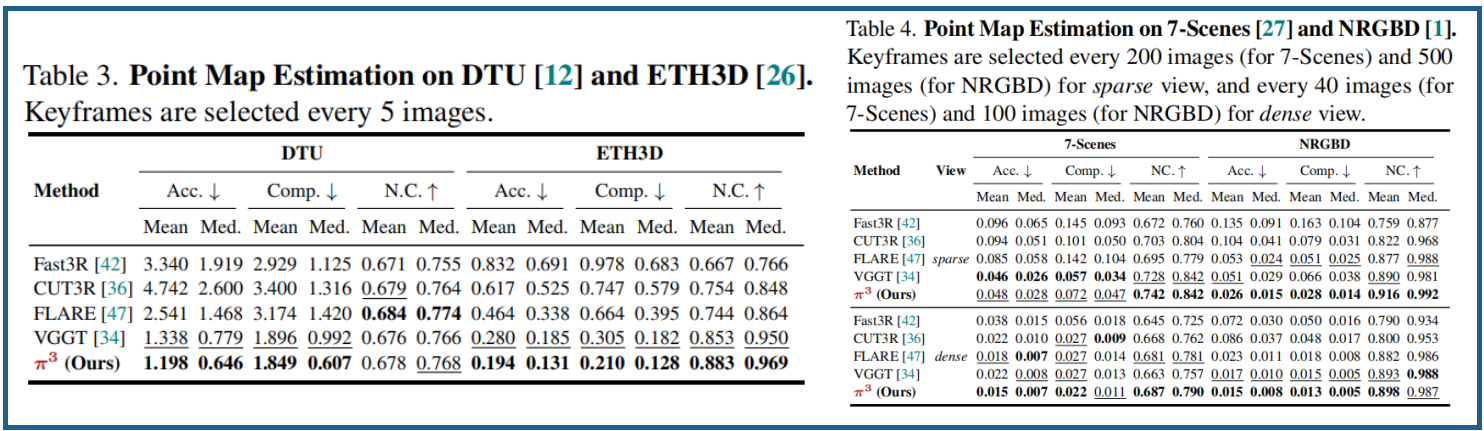
  根据VGGT，数据集为场景级7-Scenes [27]和NRGBD [1]数据集、物体为中心的DTU [12]和场景级ETH3D[26]数据集。稀疏视图，关键帧采样步长设为200（7-Scenes）或500（NRGBD）；而密集视图则将步长缩短至40（7-Scenes）或100（NRGBD）。预测点图通过Umeyama算法进行粗略Sim(3)对齐，随后使用迭代最近点（ICP）算法进行精修。

  

  

5.3 视频深度估计

  在Sintel [3]、Bonn [19]和KITTI [10]三个数据集上对视频深度估计任务进行评估。指标包含绝对相对误差（Abs Rel）及预测准确率在阈值δ < 1.25时的表现。评估指标基于两种对齐设置：(i)仅尺度对齐；（ii）联合尺度与三维平移对齐。在KITTI数据集上以57.4帧/秒的帧率运行，显著快于VGGT (43.2帧/秒）和Aether (6.14帧/秒），尽管模型规模更小

  

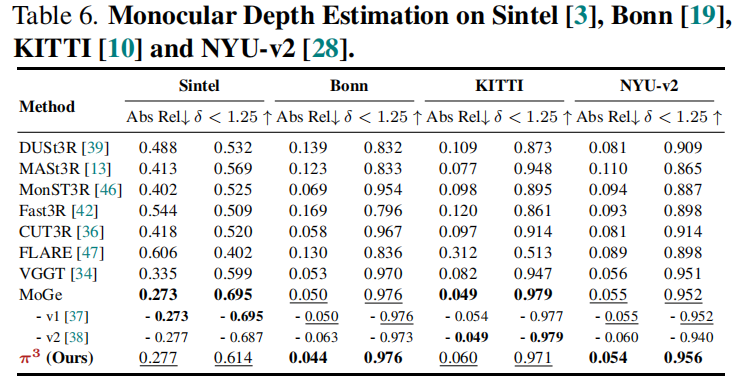
5.4 单目深度估计

  参照VGGT的四个数据集，评估尺度不变性单目深度的准确性。指标绝对相对误差（Abs Rel）和阈值准确率（δ<1.25）作为评估指标。每个深度图都独立与其真实值对齐，这与视频深度评估中对整个图像序列应用单一缩放（及位移）因子的做法形成鲜明对比。

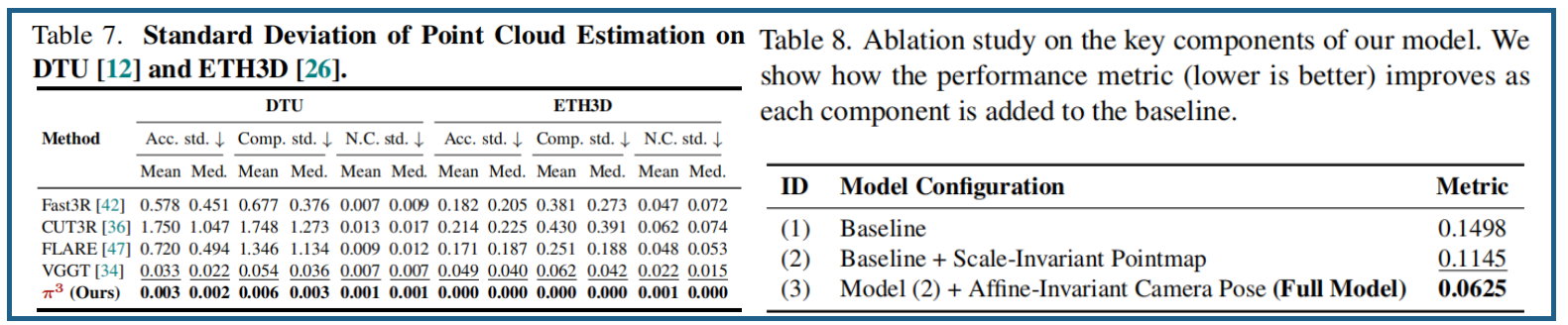
  消融实验：