计算机图像学05 几何

---

0、前言

  经过了之前的学习，我们能够表现直线、平面，接下来的几何部分，就是关于如何表示曲线、曲面的部分，首先，几何有两种表示方法，一种的隐式表示，一种是显式表示，类似于数学中的隐函数与显函数的关系，隐式表示虽然无法精确的获得每一个点的对应关系，但通常对于判断某一给定的点是否在曲线上或曲面上（内外）十分方便，显示表示则是直接用方程表示了每一个点的映射关系，但对于判断某点是否在曲线上或曲面上有时十分困难。因此，具体使用哪种表示方法需要根据现实情况决定。

1、几何的隐式表示

1.1 几何表面

  此种方法使用一方面来表示几何表面，但能表示的几何表面通常比较简单，如下所示

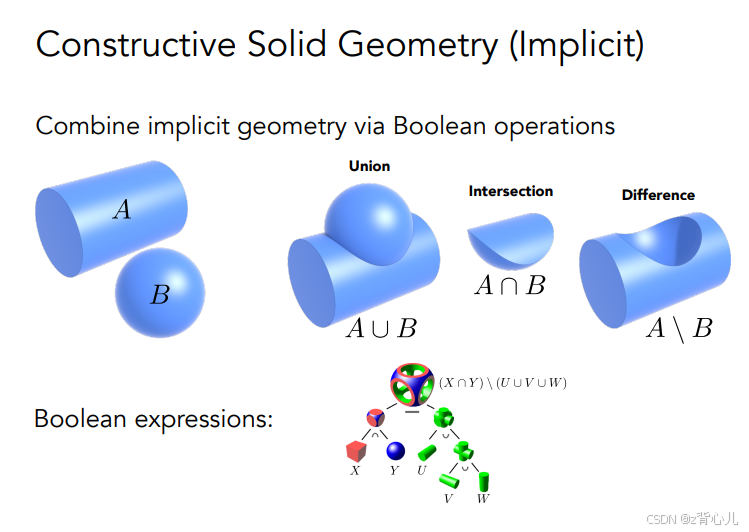
1.2 CSG（Constructive Solid Geometry）

  通过布尔表达式（逻辑关系）来组合物体进行表示，如下所示

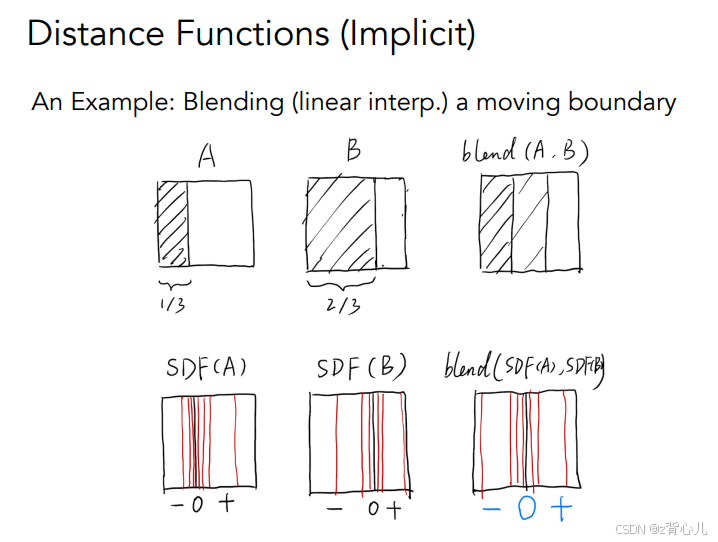
1.3 距离函数（Distance Function）

  距离函数定义为某一点到物体表面的最短距离，通过将某点到两个（或多个）物体的距离函数进行融合，再通过融合后的距离函数反向推导即可得到融合后的物体，如下所示。

1.4 水平集（Level Set Method）

与1.1几何表面类似，只是将方程表示改为了用矩阵表示

1.5 分形——自相似（Fractals)

  用自己表示自己，使用自己的复制体无限组合

2、几何的显式表示

  几何的显式表示同样有很多方法，如多边形面（Polygon Mesh）、点云（Point Cloud）等等，下面重点介绍贝塞尔曲线，和贝塞尔曲面。
  此外，额外补充一下.obj格式存储的数据内容，可分为四部分，分别是顶点坐标、法线、纹理坐标以及他们之间的连接关系，如下所示

2.1 贝塞尔曲线（Bezier Curves）

2.1.1 构造过程

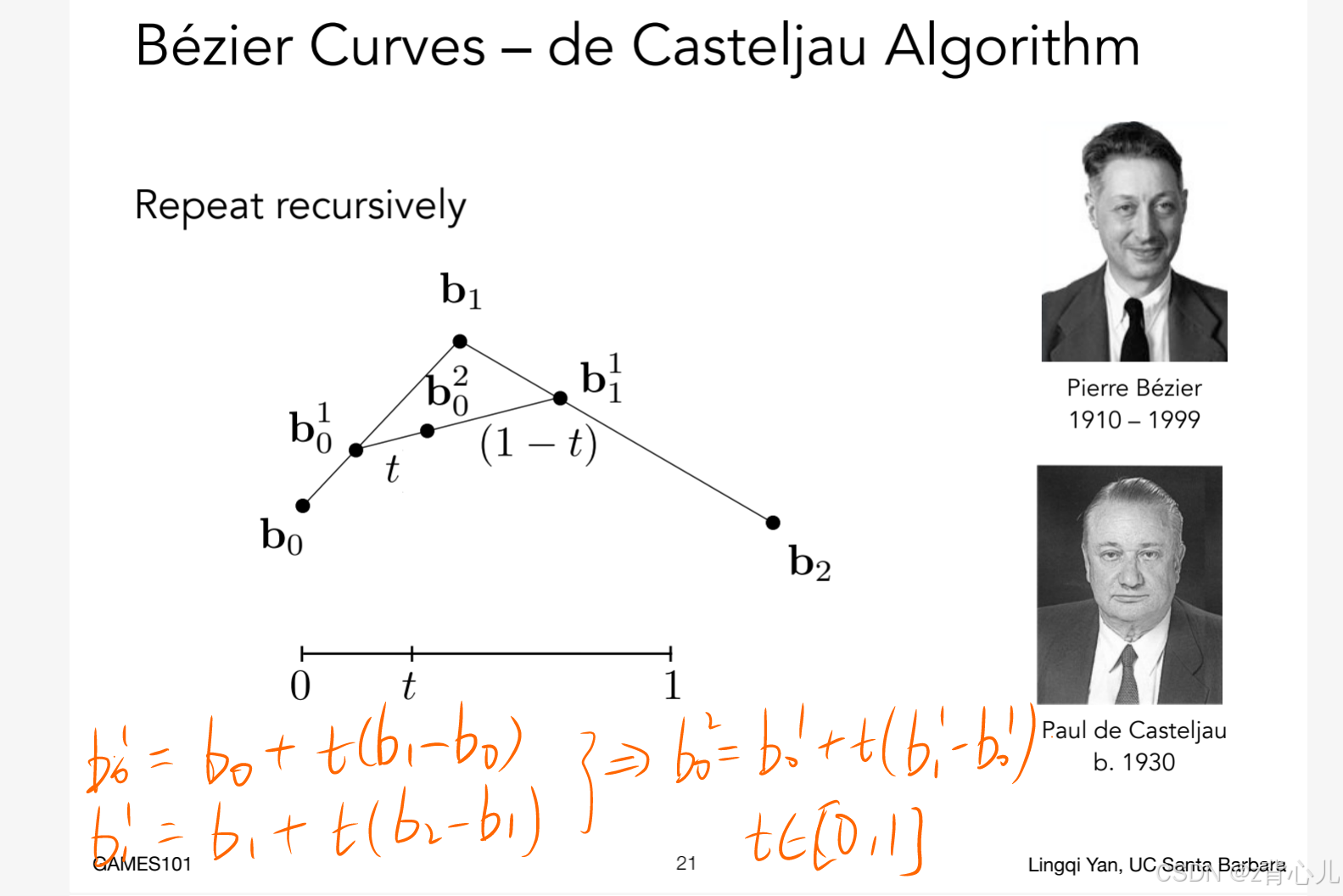
  贝塞尔曲线是通过一系列控制点构造出曲线的过程，构造过程如下，以三个控制点为例：
  1、首先，曲线的起点和终点与控制点的起点与重点相同；
  2、曲线起点与终点的切线方向满足$t_0=3(b_1-b_0)$，$t_1=3(b_2-b_1)$
  3、接下来，在$b_0{b}_1$两点之间做lerp得到$b_0^1$，$b_1{b}_2$两点之间做lerp得到$b_1^1$，再在$b_0^1$$b_1^1$两点之间做lerp即可得到曲线。

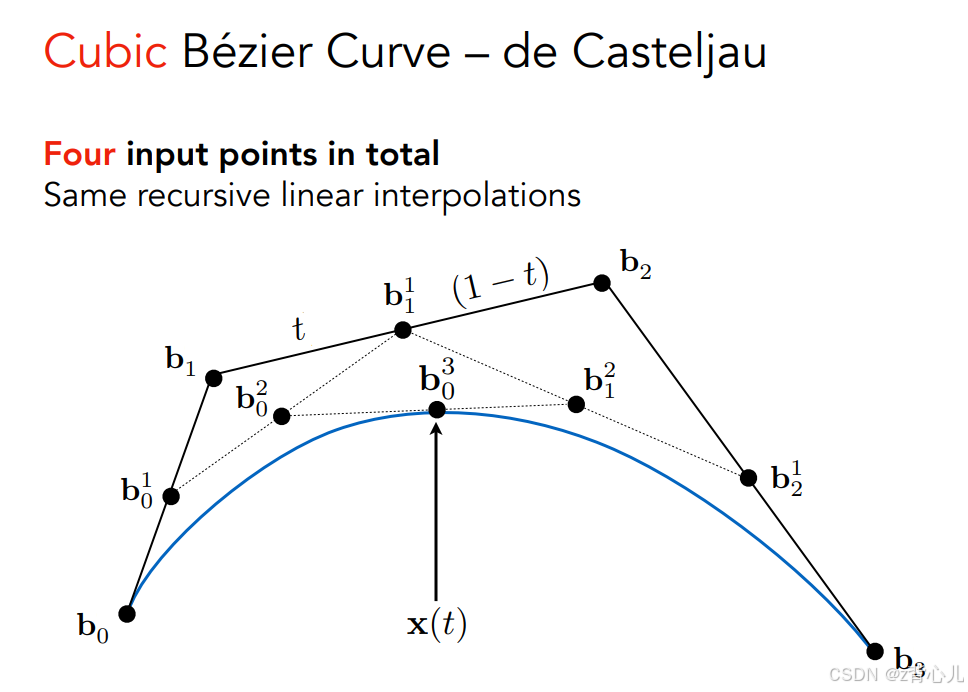
  四个控制点与三个点方法一致，只是多了几次lerp操作

2.1.2 贝塞尔曲线的公式表达

  增加控制点数目，推导可得贝塞尔曲线的公式可表示为

2.1.3 贝塞尔曲线的性质

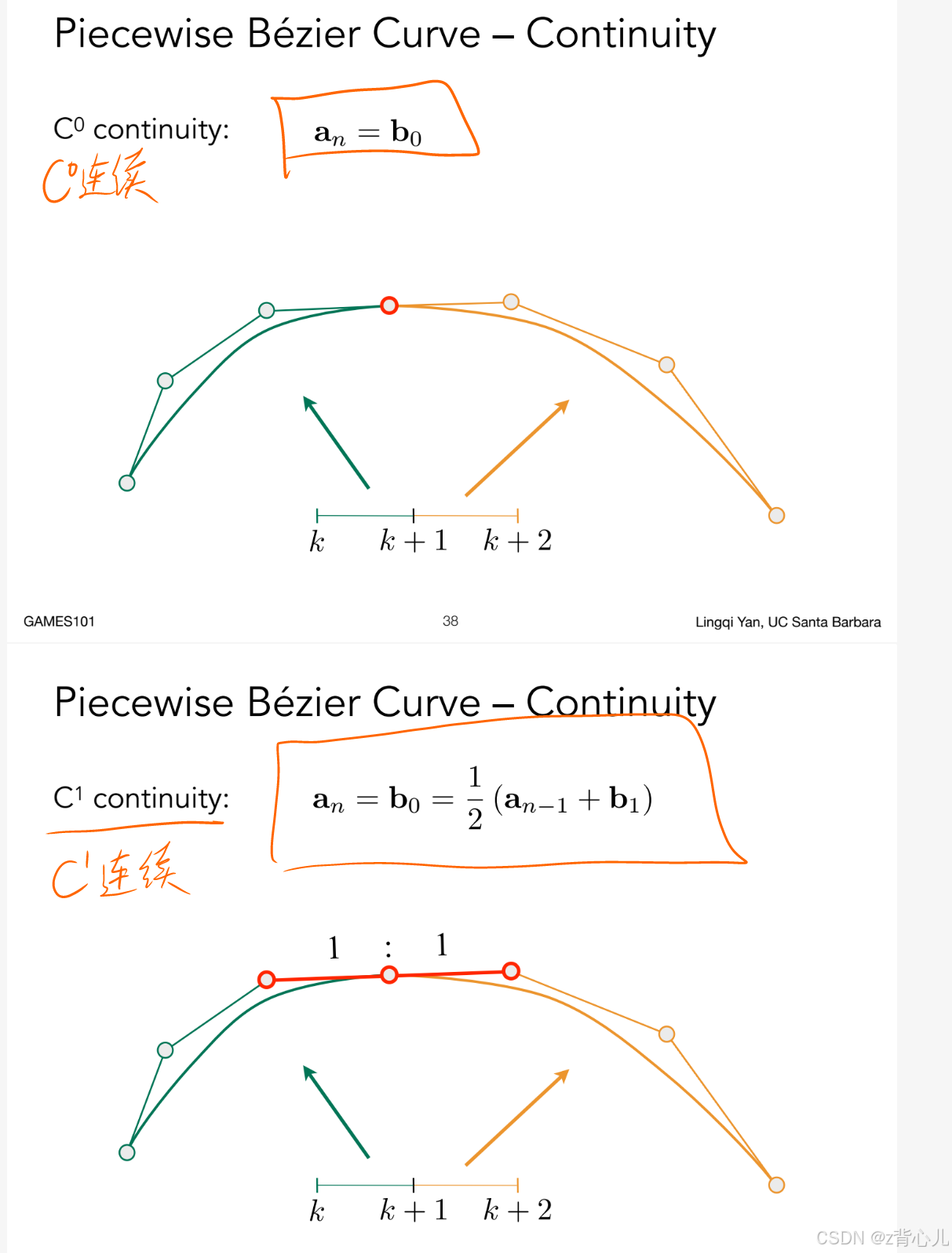
2.1.4 逐段贝塞尔曲线（Piecewise Bezier Curves)

  顾名思义，以多段贝塞尔曲线，组合成一段长曲线，每一段贝塞尔曲线通常用4个控制点，在各段贝塞尔曲线的连接点处存在连续性要求，比如$C^0$连续和$C^1$连续，定义分别如下所示

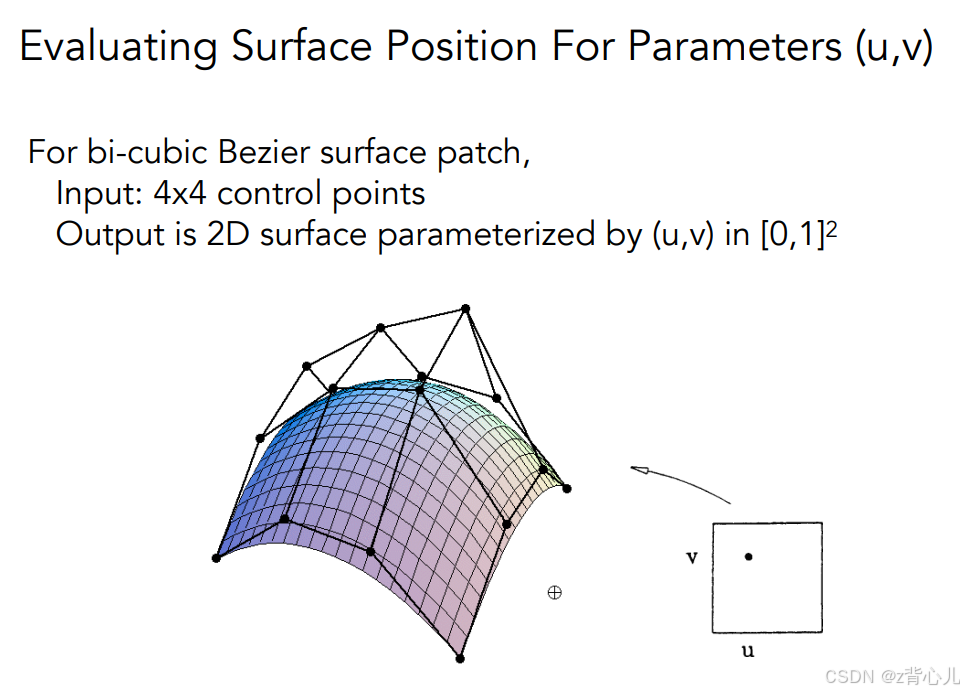
2.2 贝塞尔曲面

  有了贝塞尔曲线，就能很容易的构造贝塞尔曲面，构造方法如下（以4*4个点为例）：
  1、首先，四个控制点为一组可构造四条贝塞尔曲线（u∈[0,1])；
  2、再由这四条贝塞尔曲线上的点构造贝塞尔曲线即可得到贝塞尔曲面(v∈[0,1])。

3、几何处理——网格操作（Mesh Operations)

  Mesh Operations可分为三类，分别是网格细分（Mesh subdivision）、网格简化（Mesh simplification）、网格正则化（Mesh regularization）。效果如下所示

3.1 Mesh subdivision

  网格细分就是增加三角形的数量，以此增加分辨率。介绍两种细分方法，分别是Loop subdivision（对三角形）和 Catmull-Clark subdivision（多边形都可）。

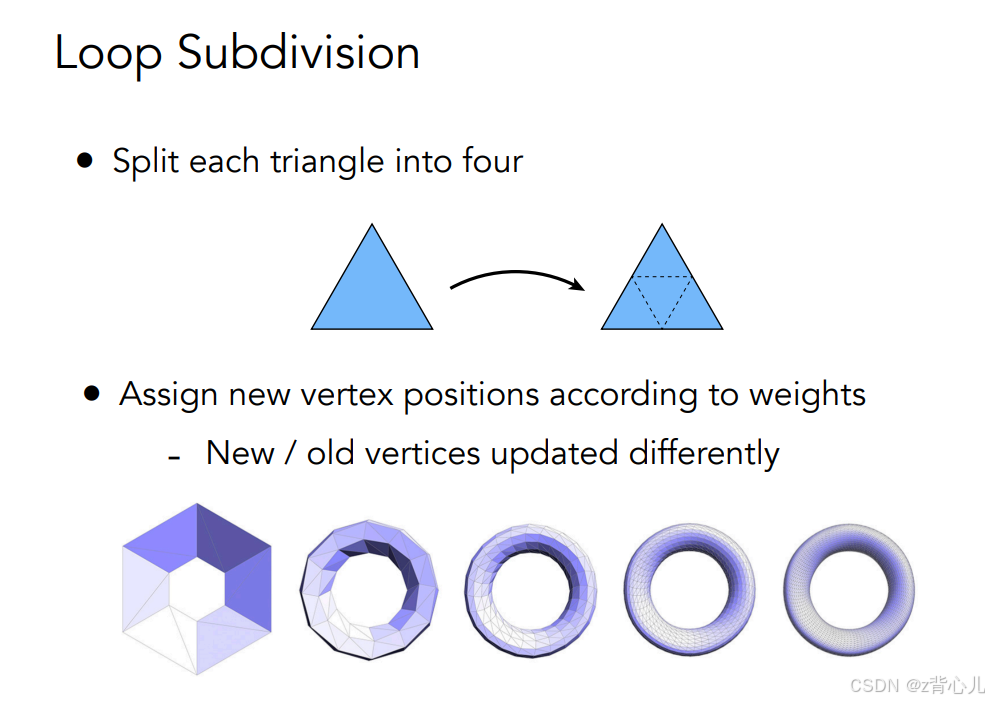
3.1.1 Loop subdivision

  Loop subdivision可分为如下两步，
  1、增加三角形的数量（将一个三角形变为四个——在三角形的每条边上取中点，再将三个中点连接起来）
  2、调整点的位置。

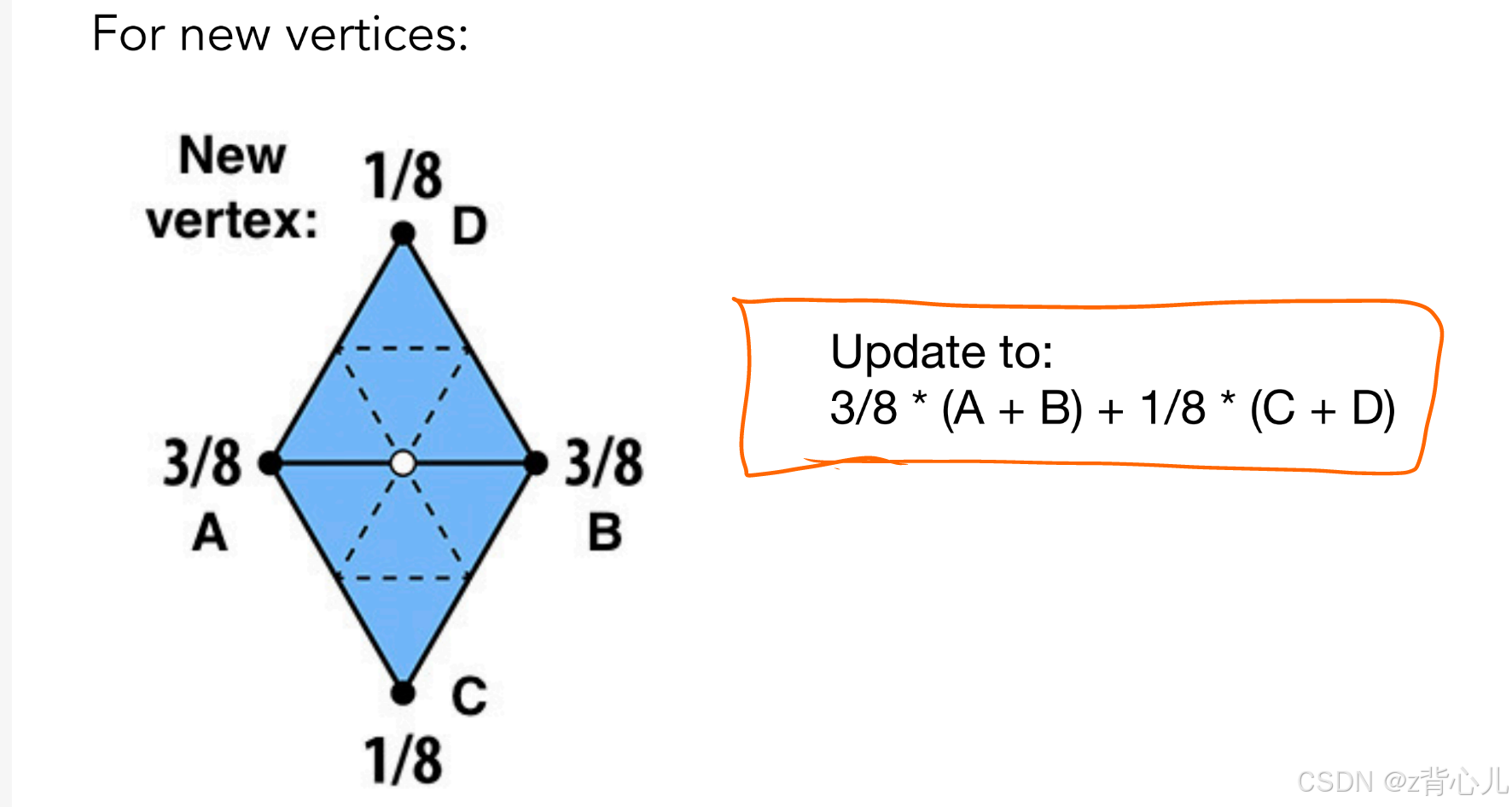
如何调整点的位置呢，首先将点分为两类，分别是新增的点（即中点）和旧点，再对这两类点分别采用如下方法进行调整

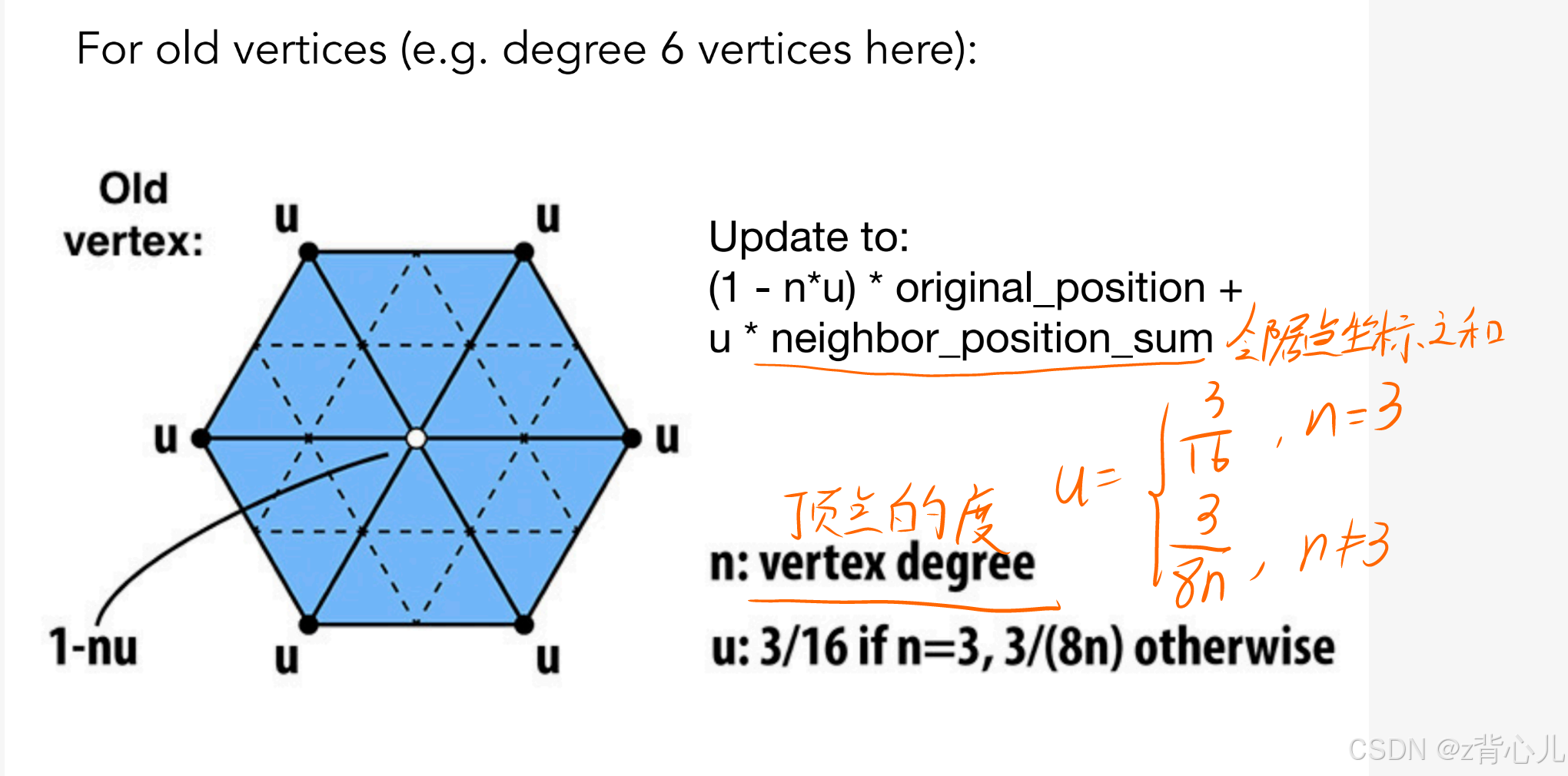
3.1.2 Catmull-Clark subdivision

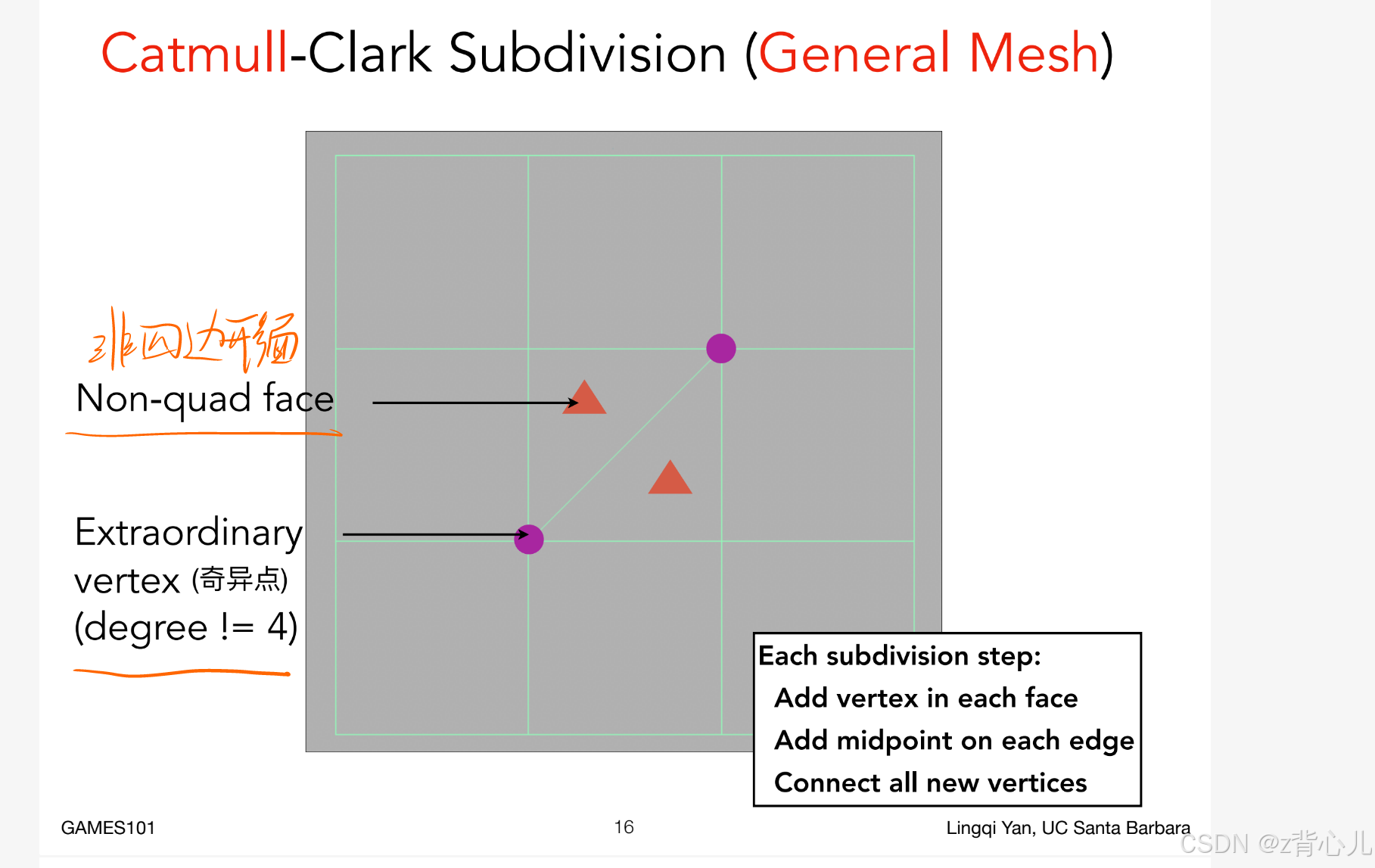
  首先，对于如下的多边形网格，其中的网格可分为两类，由四条边组成的四边形面和不是由四边形组成的非四边形面（Non-quad face），点也可分为两类，度为4的点和度不为4的点（奇异点——Extraordinary vertex),细分步骤如下：
  1、在每个面的中心增加一个点；
  2、在每条边的中点增加一个点；
  3、连接所有的新增点。


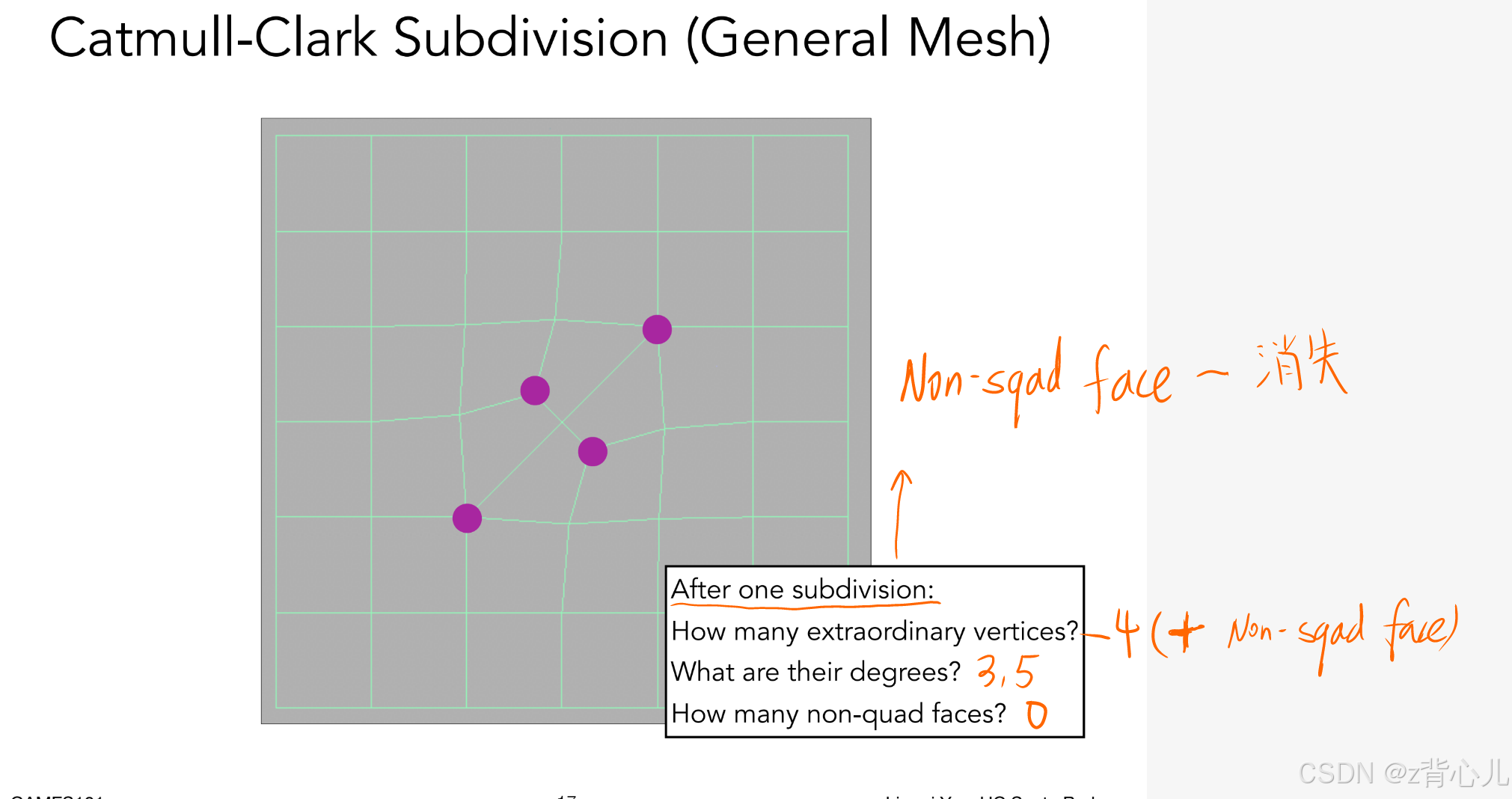
可见，经过第一次细分过后，非四边形面都消失了，变成了四边形面，奇异点的数目增加了，增加的数目为消失非四边形面的数目，此后无论再经过几次细分，奇异点数目都将不再变化。
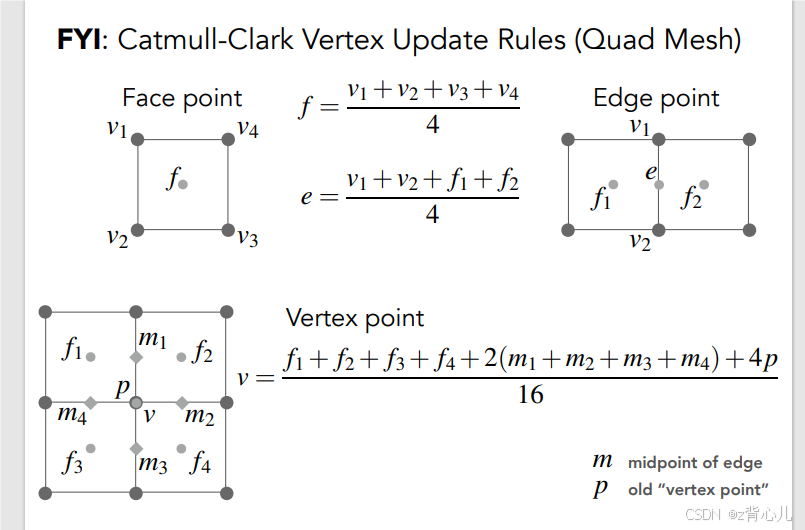
  细分后点的位置更新规则如下所示

3.2 Mesh simplification

  网格简化即减少三角形的数目，以此减小分辨率。采用的方法是坍缩边（即删掉一条边，再将与此边关联的各条边相连），如下所示

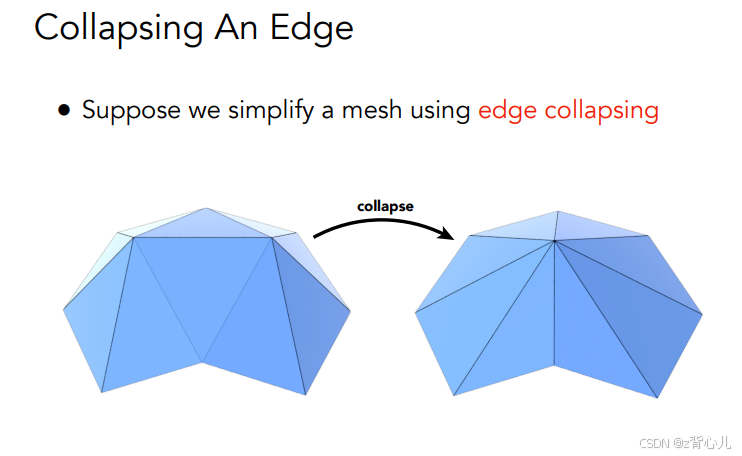
  问题是在简化过程中，应该删掉拿一条边，首先定义二次度量误差如下，那么很简单，对于每一条边，求出他的二次度量误差，再删除二次度量误差最小的拿一条边即可，此后更新与此边关联的边的二次度量误差，再删除二次度量误差最小的那天边，再更新…，循环往复直到简化到满足要求。

4、补充：Shadow Mapping

4.1 Shadow Mapping方法

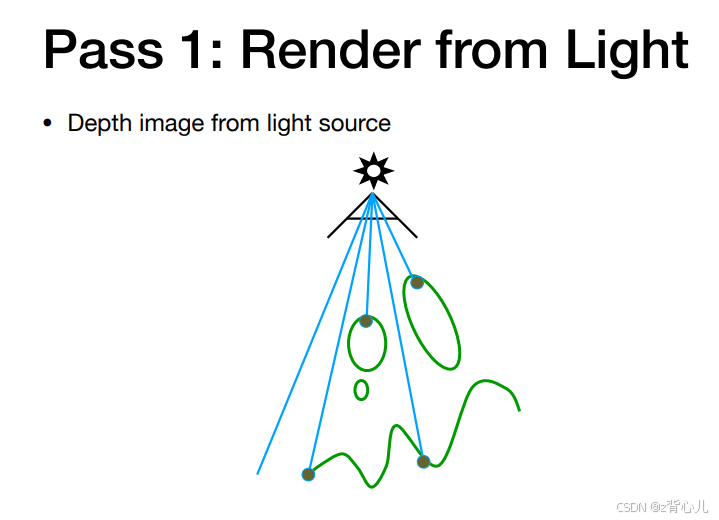
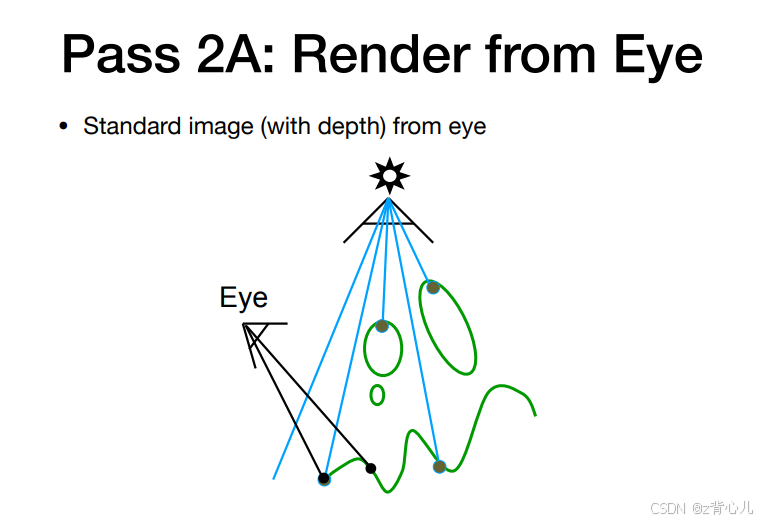
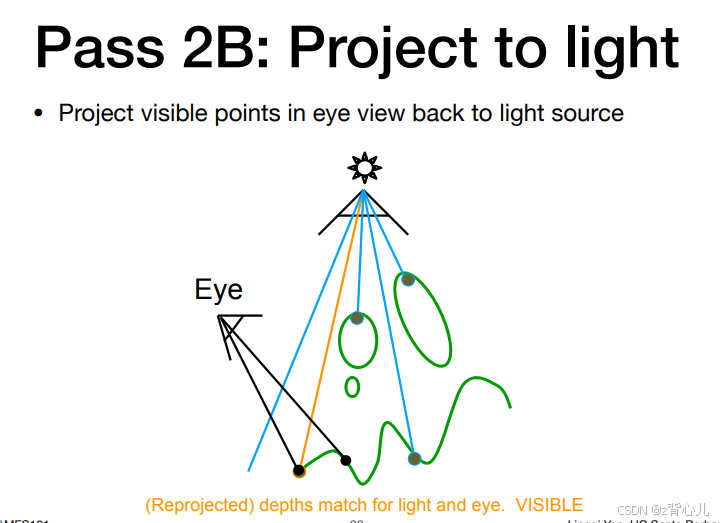
  在此前光栅化和渲染中，我们已经能够渲染处物体的纹理，表面的光照，但还没有对阴影进行渲染，因此，shadow mapping就是渲染阴影的方法，他的核心思想是：首先定义非阴影区域，若一个点不是阴影，那么这个点一定能被光源看到、同时能被人眼（摄像头）看到。
  因此，shadow mapping分为两步，第一步是得到在光源处场景的深度图，第二步是得到在人眼（摄像头）处场景的深度图，再将此深度图投影到光源坐标系下，比较两图相同点处的深度，若深度相同，说明这个点为非阴影点，若不同，说明此点是阴影。

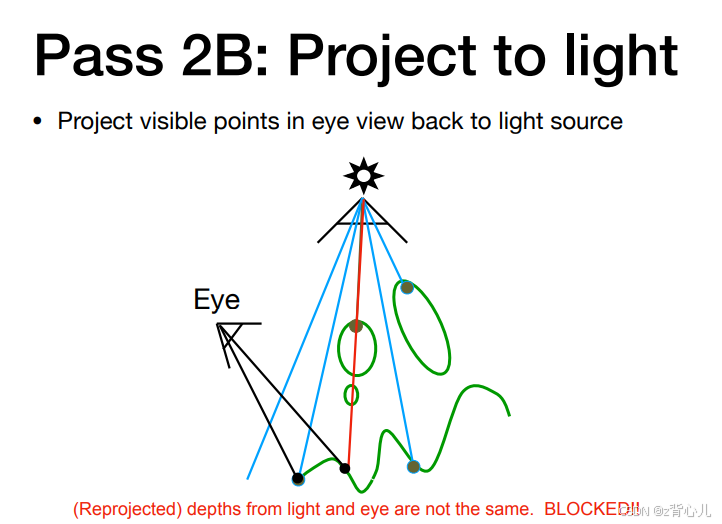
4.2 Shadow Mapping的问题

  使用Shadow Mapping得到的阴影
  1、是硬阴影，属于非黑即白式的，缺少过渡；
  2、阴影的质量取决于shadow map的分辨率；
  3、涉及浮点深度值的相等比较，意味着尺度、偏差和容差的问题。
  硬阴影和软阴影的比较如下所示