《具体数学》部分习题解答3

3.1

在第一章分析约瑟夫问题时，将任意的一个正整数 $n$ 表示成了 $n=2^m+l$ 的形式，其中 $0\le l<2^m$ 。请利用底括号或顶括号，给出将 $l$ 和 $m$ 表示成为 $n$ 的函数的显式公式

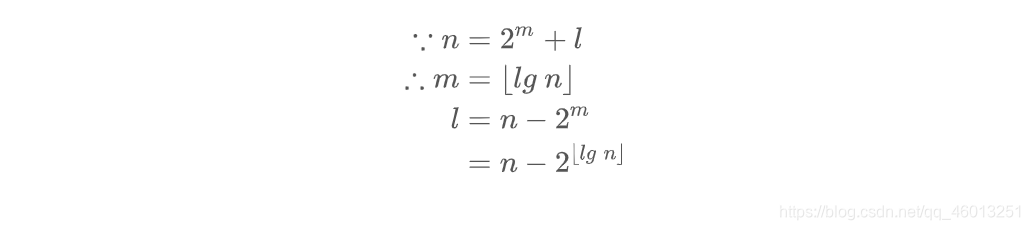
3.2

与一个给定实数 $x$ 距离最近的整数的公式是什么？在对等情况下，$x$ 恰好在两个整数的中间位置，请给出一个表达式，它（ $a$ ）往上舍入成整数，即成为 $\lceil x\rceil$ ;（ $b$ ）向下舍入成整数，即成为 $\lfloor x\rfloor$ 。

不失一般性，假设 $x$ 位于 $n$ 和 $n+1$ 之间。
$a$ 种情况下，仅当 $x\in [n,n+0.5)$ 时，答案是 $n$ ，否则为 $n+1$ ，因此将 $x$ 加上0.5再向下取整。
$b$ 种情况下，仅当$x\in [n,n+0.5]$ 时，答案是 $n$ ，否则为 $n+1$ ，因此将 $x$ 减去0.5再向上取整。
$$\begin{gathered} a.\lfloor x+0.5\rfloor \\ b.\lceil x-0.5\rceil \end{gathered}$$

3.3

当 $m$ 和 $n$ 是正整数，且 $\alpha$ 是大于 $n$ 的无理数时，计算 $\lfloor \lfloor m\alpha \rfloor n/\alpha \rfloor$

3.5

当 $n$ 是正整数时，求使得 $\lfloor nx\rfloor =n\lfloor x\rfloor$ 成立的必要充分条件。（你的条件应该包含 { x } \{x\} {x} ）

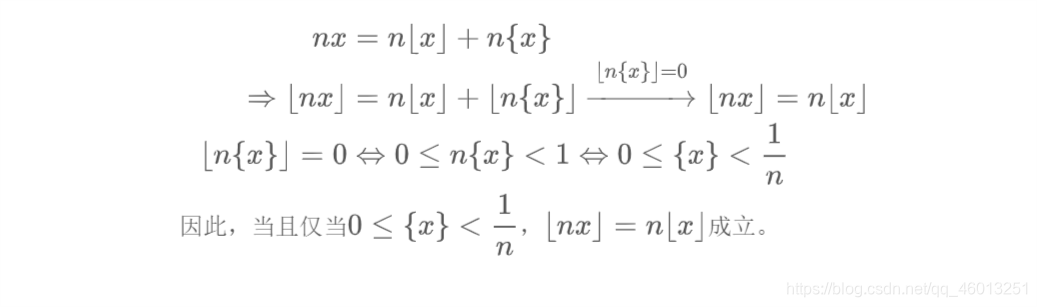
3.6

当 $f(x)$ 是仅当 $x$ 为整数时才取整数值的连续单调递减函数时，关于 $\lfloor f(x)\rfloor$ 有什么可谈的吗？

3.7

解递归式
$$\begin{gathered} X_n=n,0\le n<m \\ {X}_n=X_{n-m}+1,n\ge m \end{gathered}$$

不妨列出部分 $X_n$ 的值：

n	0	1	2	3	$\dots$	m-1	m	m+1	$\dots$	2m	2m+1	$\dots$
$X_n$	0	1	2	3	$\dots$	m-1	1	2	$\dots$	2	3	$\dots$

由此可以发现 $X_n$ 的规律并写出表达式： $X_n=nmodm+\lfloor \frac{n}{m}\rfloor$

3.8

证明狄利克雷抽屉原理：如果 $n$ 个物体放进 $m$ 个盒子中，那么某个盒子中必定含有 $\ge \lceil n/m\rceil$ 个物体，且有某个盒子中必定含有 $\le \lfloor n/m\rfloor$ 个物体。

反证法：假设所有盒子中含有 $<\lceil \frac{n}{m}\rceil$ 个物体，也即含有 $\le (\lceil \frac{n}{m}\rceil -1)$ 个物体，因此，总共 $m$ 个盒子一共含有 $\le m(\lceil \frac{n}{m}\rceil -1)$ 个物体，有： $\frac{n}{m}+1\le \lceil \frac{n}{m}\rceil$ ，矛盾，假设不成立，即证某个盒子中必定含有 $\ge \lceil n/m\rceil$ 个物体。
同理可证某个盒子中必定含有 $\le \lfloor n/m\rfloor$ 个物体。

3.10

证明，表达式
$$\lceil \frac{2x+1}{2}\rceil -\lceil \frac{2x+1}{4}\rceil +\lfloor \frac{2x+1}{4}\rfloor$$
总是等于 $\lfloor x\rfloor$ 或者 $\lceil x\rceil$ ，每一种情形在何时会出现？

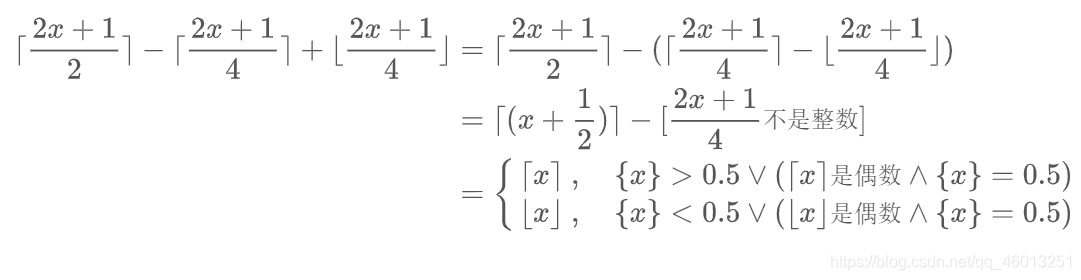
3.11

给出正文中提及的证明细节：当 $\alpha <\beta$ 时，开区间 $(\alpha ,\beta )$ 恰好包含 $\lceil \beta \rceil -\lfloor \alpha \rfloor -1$ 个整数。为使证明正确，为什么 $\alpha =\beta$ 的情形必须排除在外？

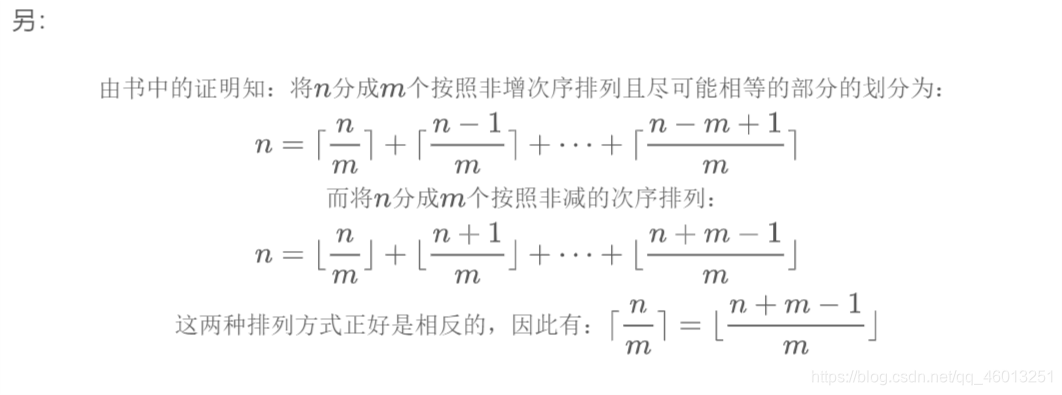
3.12

证明，对所有整数 $n$ 和所有正整数 $m$ 有
$$\lceil \frac{n}{m}\rceil =\lfloor \frac{n+m-1}{m}\rfloor$$
（这个恒等式给出了另一种将顶与底相互转化的方法，它用不到反射律）

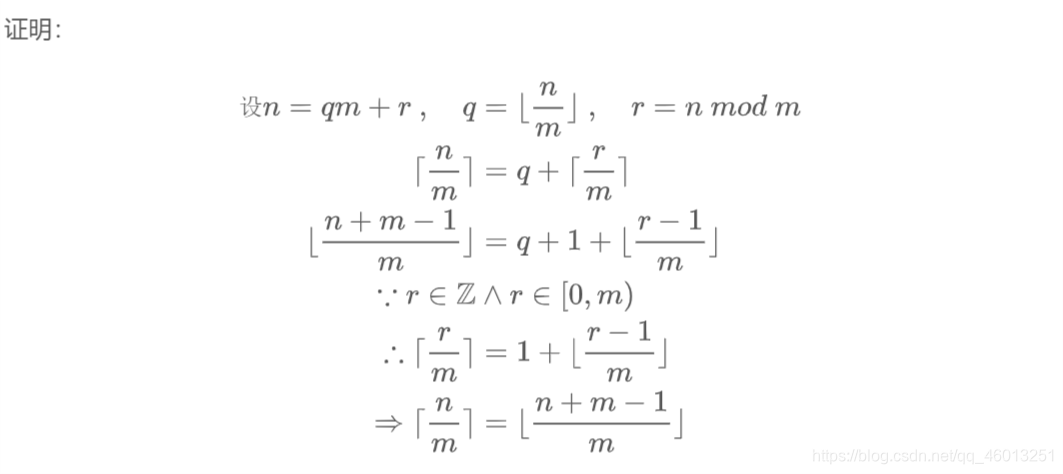
3.14

证明或推翻： $(xmodny)mody=xmody,n为整数$

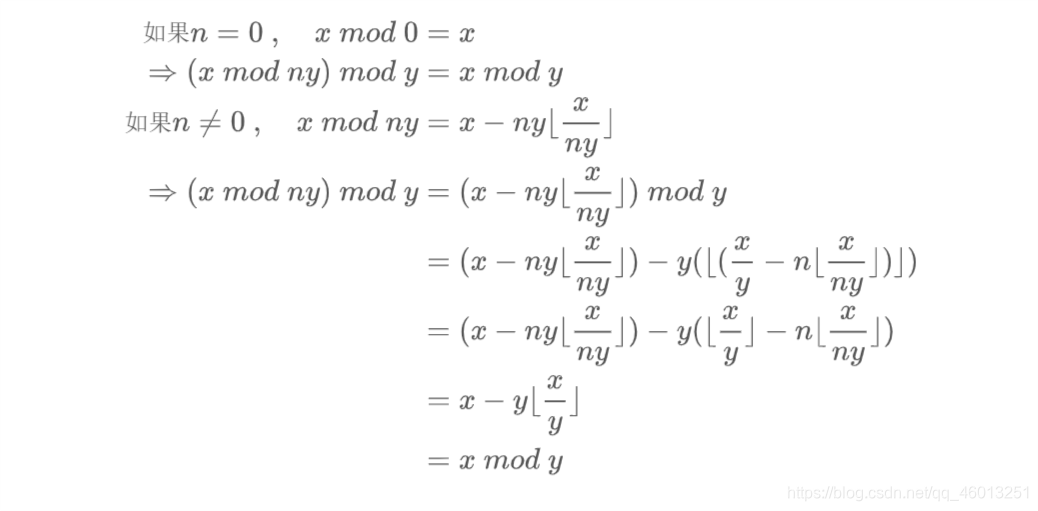
3.15

存在与
$$\lfloor mx\rfloor =\lfloor x\rfloor +\lfloor x+\frac{1}{m}\rfloor +\cdots +\lfloor x+\frac{m-1}{m}\rfloor$$
类似的用顶替代底的恒等式吗？

$$\begin{gathered} 已知：n=\lceil \frac{n}{m}\rceil +\lceil \frac{n-1}{m}\rceil +\cdots +\lceil \frac{n-m+1}{m}\rceil \\ 用\lceil mx\rceil 替换n，得到： \\ \lceil mx\rceil =\lceil x\rceil +\lceil x-\frac{1}{m}\rceil +\cdots +\lceil x-\frac{m-1}{m}\rceil \end{gathered}$$

3.16

证明 $nmod2=(1-(-1{)}^n)/2.$ 对 $nmod3$ 求出并证明类似的形如 $a+b{\omega }^n+c{\omega }^{2n}$ 的表达式，其中 $\omega$ 是复数 $(-1+i\sqrt{3})/2$ 。提示： ${\omega }^3=1$ 且 $1+\omega +{\omega }^2=0$

$$\begin{gathered} n无非是两种情况：n=2k或n=2k+1,其中k\in \mathbb{Z} \\ 如果n=2k，则nmod2=\frac{1-(-1{)}^{2k}}{2}=0 \\ 如果n=2k+1，则nmod2=\frac{1-(-1{)}^{2k+1}}{2}=1 \\ 无论哪种情况等式均成立。 \end{gathered}$$
同理：

3.17

在 $x\ge 0$ 的情况下，通过用 ${\sum }_j[1\le j\le x+k/m]$ 替换 $\lfloor x+k/m\rfloor$ 并首先对 $k$ 求和，来计算和式 ${\sum }_{0\le k<m}\lfloor x+k/m\rfloor$ 。你的答案与 $\lfloor mx\rfloor =\lfloor x\rfloor +\lfloor x+\frac{1}{m}\rfloor +\cdots +\lfloor x+\frac{m-1}{m}\rfloor$吻合吗？

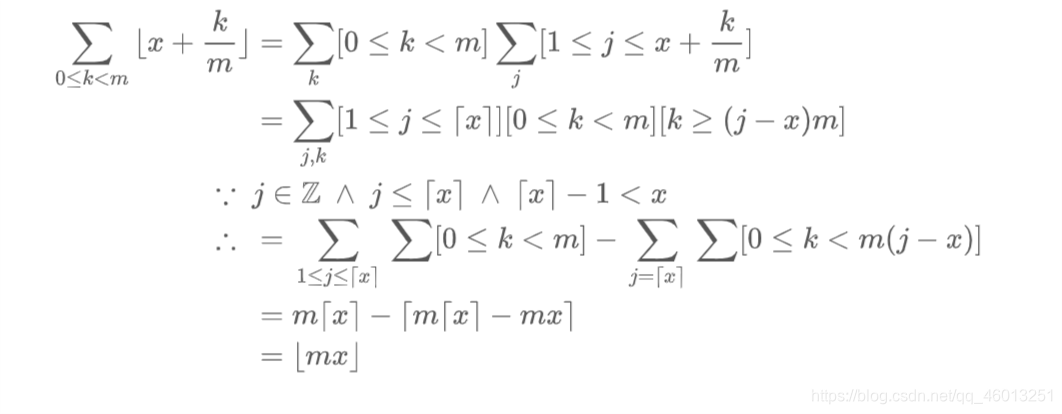
3.19

求出关于实数 $b>1$ 的一个必要充分条件，使得
$$\lfloor {\log }_{b}x\rfloor =\lfloor {\log }_b\lfloor x\rfloor \rfloor$$
对所有实数 $x\ge 1$ 都成立

3.20

当 $x>0$ 时，求闭区间 $[\alpha \dots \beta ]$ 中 $x$ 的所有倍数之和

$$\begin{gathered} \lceil \frac{\alpha }{x}\rceil 代表闭区间中首个x的倍数 \\ \lfloor \frac{\beta }{x}\rfloor 代表闭区间中最后一个x的倍数 \\ 因此有：\sum _{k=\lceil \frac{\alpha }{x}\rceil }^{\lfloor \frac{\beta }{x}\rfloor }kx=\frac{x}{2}((\lfloor \frac{\beta }{x}\rfloor {)}^2+\lfloor \frac{\beta }{x}\rfloor -(\lceil \frac{\alpha }{x}\rceil {)}^2+\lceil \frac{\alpha }{x}\rceil ) \end{gathered}$$

3.21

对 $0\le m\le M$ ，有多少个数 $2^m$ 的十进制表示中，其首位数字为1？

$$\begin{gathered} 在十进制表示中，如果首位数字为1,对应该数字为10的幂 \\ 而在[10^n,2\ast 10^n)中一共有(\lceil \lg 2+n\lg 10\rceil -\lceil n\lg 10\rceil )个2的幂，即一个2的幂 \\ 问题即转换为：对于0\le m\le M，2^m中有多少个10的幂？ \\ 因此答案为：\lfloor \log 2^M\rfloor +1 \end{gathered}$$

3.22

计算和式 $S_n={\sum }_{k\ge 1}\lfloor n/2^k+\frac{1}{2}\rfloor$ 以及 $T_n={\sum }_{k\ge 1}{2}^k\lfloor n/2^k+\frac{1}{2}{\rfloor }^2.$

3.23

证明序列
$$1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,\dots$$
的第 $n$ 个元素是 $\lfloor \sqrt{2n}+\frac{1}{2}\rfloor$ （这个序列恰好包含 $m$ 个 $m$）

3.25

证明或推翻：对所有非负的 $n$ ，由
$$\begin{gathered} K_0=1 \\ {K}_{n+1}=1+min(2K_{\lfloor n/2\rfloor },3K_{\lfloor n/3\rfloor }),n\ge 0 \end{gathered}$$
所定义的高德纳数满足 $K_n\ge n$.

3.26

证明：辅助的约瑟夫数满足：
$$(\frac{q}{q-1}{)}^n\le D_n^{(q)}\le q(\frac{q}{q-1}{)}^n,n\ge 0$$

辅助的约瑟夫数：
$$\begin{gathered} D_0^{(q)}=1 \\ {D}_n^{(q)}=\lceil \frac{q}{q-1}{D}_{n-1}^{(q)}\rceil ,n>0 \end{gathered}$$
在辅助的约瑟夫数中，$q$ 应该是正整数.

用数学归纳法证明：
第一个 $\le$ 号：
$$\begin{gathered} 假设(\frac{q}{q-1}{)}^{n-1}\le D_{n-1}^{(q)} \\ 则：D_n^{(q)}=\lceil \frac{q}{q-1}{D}_{n-1}^{(q)}\rceil \ge \lceil (\frac{q}{q-1}{)}^n\rceil \ge (\frac{q}{q-1}{)}^n \end{gathered}$$
第二个 $\le$ 号：
$$\begin{gathered} 假设D_{n-1}^{(q)}\le q(\frac{q}{q-1}{)}^{n-1}-(q-1)\le q(\frac{q}{q-1}{)}^{n-1} \\ {D}_n^{(q)}=\lceil \frac{q}{q-1}{D}_{n-1}^{(q)}\rceil \le \lceil q(\frac{q}{q-1}{)}^n-q\rceil \\ \iff D_n^{(q)}\le q(\frac{q}{q-1}{)}^n+1-q\le q(\frac{q}{q-1}{)}^n \end{gathered}$$

3.30

证明：如果 $m$ 是一个大于2的整数，其中 $\alpha +{\alpha }^{-1}=m$ 且 $\alpha >1$，那么递归式

有解 $X_n=\lceil {\alpha }^{2^n}\rceil .$ 例如，如果 $m=3$, 则解为：
$$X_n=\lceil {\varphi }^{2^{n+1}}\rceil ,\varphi =\frac{1+\sqrt{5}}{2},\alpha ={\varphi }^2$$

3.31

证明或推翻： $\lfloor x\rfloor +\lfloor y\rfloor +\lfloor x+y\rfloor \le \lfloor 2x\rfloor +\lfloor 2y\rfloor .$

3.34

设 $f(n)={\sum }_{k=1}^n\lceil \lg k\rceil .$

3.35

化简公式 $\lfloor (n+1{)}^{2}n!e\rfloor modn$.

3.45

如果 $m$ 是一个正整数，推广习题30的技巧来求

的封闭形式的解

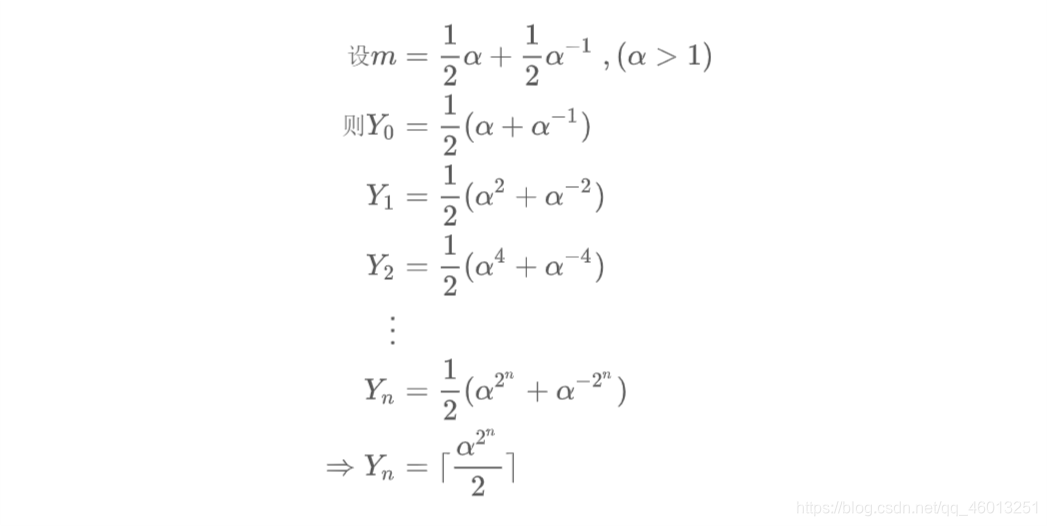
如有问题，欢迎大家指出，谢谢