第五章
1. 证明：每个k方体都有完美匹配；(2)求 K 2 n K_{2n} K2n 和 K n , n K_{n, n} Kn,n 中不同的完美匹配的个数。
2. 证明：一棵树最多只有一个完美匹配。
3. 对每个 k > 1 k>1 k>1，找出一个没有完美匹配的 k k k 正则简单图的例子,（不太懂）
4. 证明： K 4 K_4 K4 有唯一的一个 1-因子分解。
K 8 K_8 K8 的所有一因子分解如下：
5. 求 K 3 , 3 K_{3,3} K3,3 和 K 6 K_6 K6 的 1-因子的个数。
K 3 , 3 = 3 ! = 6 K_{3,3} = 3! = 6 K3,3=3!=6
K
6
=
5
×
3
×
1
=
15
K_6 = 5 × 3 × 1 = 15
K6=5×3×1=15
6. 证明: K 2 n K_{2n} K2n 的不同的 1-因子的数目为 ( 2 n ) ! 2 n n ! \frac{(2n)!}{2^nn!} 2nn!(2n)!。
7. 将 K 9 K_9 K9 表示为四个生成圈之和
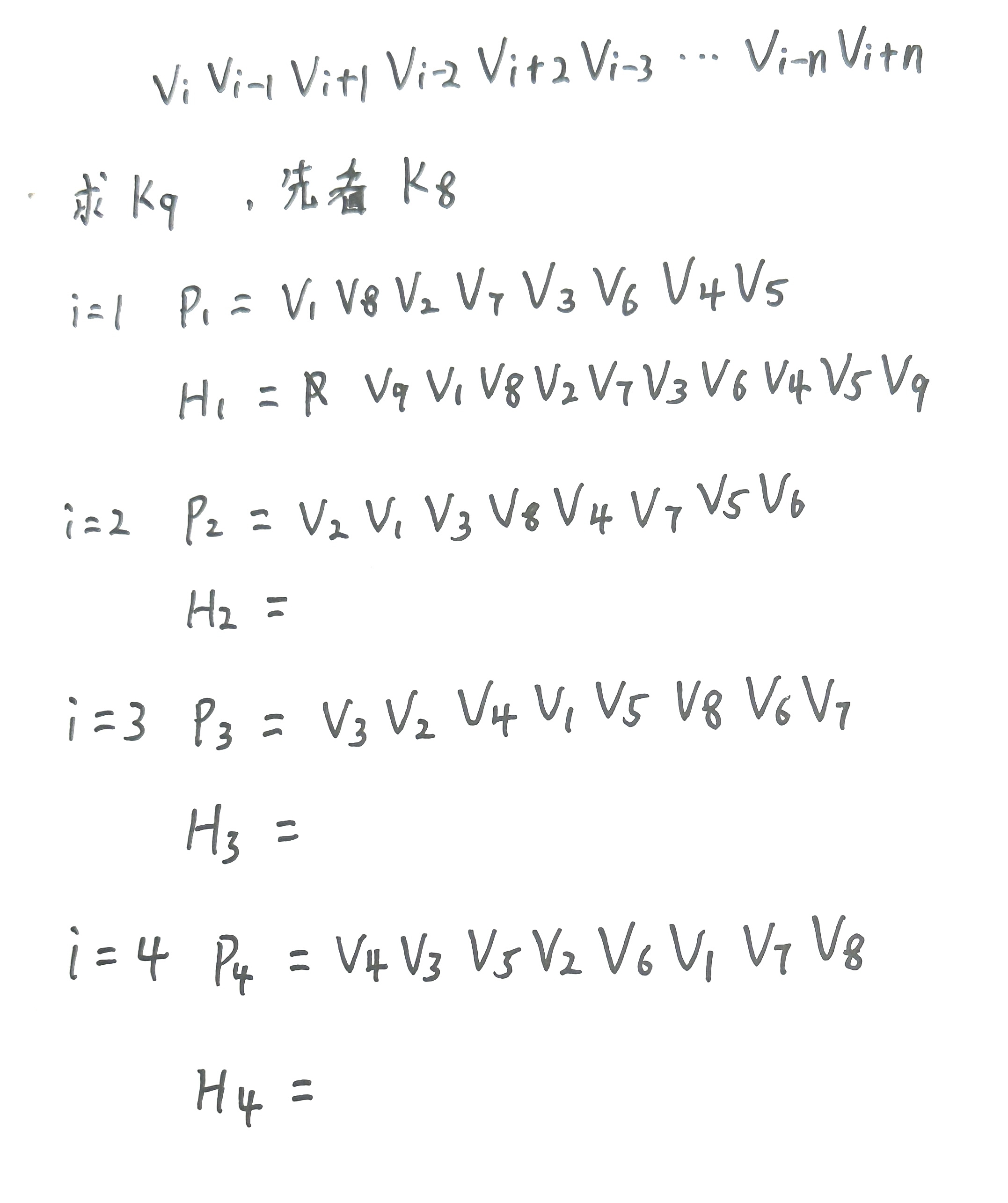
8. 证明: K 6 n − 2 K_{6n-2} K6n−2 有一个 3-因子分解。
10. 证明：若 n n n 是偶数且 δ ( G ) ⩾ n / 2 + 1 \delta(G)\geqslant n/2+1 δ(G)⩾n/2+1, 则 n n n 阶简单图 G G G 有 3-因子。
11. 对 k > 0 k>0 k>0，证明 (1) 每个 k k k 正则偶图是 1-可因子分解的; (2) 每个 2 k 2k 2k 正则图是 2-可因子分解的。
12. 证明：一棵树 T 有完美匹配当且仅当 o ( T − v ) = 1 o(T-v)=1 o(T−v)=1 对所有的 v ∈ V ( T ) v \in V(T) v∈V(T) 成立。
13
15.
18.
下面这个图有割边有完美匹配
- C
答案：C
- A
α
\alpha
α
偶数阶完全图可一因子分解，即 K 2 n K_{2n} K2n可分解成 2 n − 1 2n-1 2n−1 个一因子，所以 K 2 ( 3 n − 1 ) K_{2(3n-1)} K2(3n−1)，可分解成 2 ∗ ( 3 n − 1 ) − 1 = 6 n − 3 2*(3n-1)-1=6n-3 2∗(3n−1)−1=6n−3 个一因子即 2 n − 1 2n-1 2n−1 个 3 3 3 因子的和
注意： 不同的一因子之间是可以并起来的。
第六章
1. 判断图6-37所示的七个图是否可平面?为什么?
2.
3.
4.
5.
6.
7.
8.
11
19.
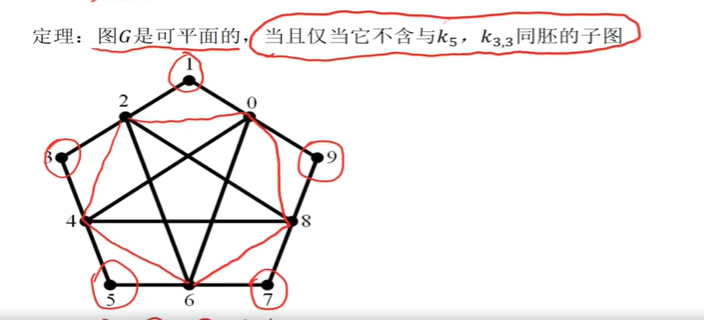
- 3
- n − m + ϕ = 2 n - m + \phi = 2 n−m+ϕ=2
- 6
- 5 连通，意味着最小度为 5，意味着
第七章作业
对于完全图 K n K_n Kn ，点着色为 Δ + 1 \Delta + 1 Δ+1，等于 n n n
五色定理
- 彼得森图的点色数是 3，边色数是 4
- n n n 阶树的点色数是 2（每条边的两个端点颜色不同即可），边色数是 Δ \Delta Δ（树不含有奇圈，因此为 Δ \Delta Δ）
- n n n 方体的点色数为 2，边色数为 n − 1 n - 1 n−1
或者是考试不冲突类问题，都属于下面这种
奇圈的点色数为 3
图中有一个几圈，点色数至少为 3，由于 LA 与奇圈每个点相连，点色数不再是 3，变为至少 4，LA 颜色不同。
然后用 4 种颜色去尝试
第八章作业
强连通分支：即提取出的一个最大能够满足双向连通的子图，如果本身是强连通的，则本身就是自己的一个强连通分支。
强连通没有割边，是因为有割边一定是单向连通的
2 m 2^m 2m 种
按照如下排列达到最小：除了最后一层 2个，其余每层 1 个，因此至少 h + 1 个树叶
常见的一些证明题
其中不等式说明含有 H 圈，n 为偶数且含有H，说明这个H可以为两个 1 因子的和，然后图 G 减去一个一因子，不断这个过程，就会有三个 1 因子 + 一个 2 因子。（注意奇数阶就不能这样做了）
和上面相同的方法
不断划分每个联通分支都是圈
反证法，
扫一扫
3287
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
